The set A={x:ax=1,a>0,ξnR} can never be
Null set
Singleton set
Finite set
Infinite set
The correct Answer is:A
To solve the problem, we need to analyze the set A={x:ax=1,a>0,x∈R} and determine the nature of this set.
1. Understanding the Equation:
The equation ax=1 holds true under certain conditions. Specifically, for any positive a, the equation ax=1 is true if x=0. This is because any non-zero number raised to the power of 0 equals 1.
Hint: Recall the properties of exponents, particularly that a0=1 for any a>0.
2. Identifying Possible Values of x:
Since ax=1 when x=0, we can conclude that x=0 is a solution. However, we must consider if there are other solutions.
Hint: Think about whether there are other values of x that can satisfy ax=1 for a>0.
3. Exploring Different Cases for a:
- If a=1, then 1x=1 for all x. Thus, the set A would contain all real numbers, making it an infinite set.
- If a>1 or 0<a<1, the only solution remains x=0. Thus, the set A would be {0}, which is a singleton set.
Hint: Analyze the behavior of the function ax for different values of a.
4. Conclusion on the Nature of Set A:
From the above analysis, we can conclude:
- If a=1, A is infinite.
- If a≠1, A is a singleton set containing just {0}.
Therefore, the set A can never be a null set (empty set) because there will always be at least one value (either all real numbers or just 0).
Hint: Remember that a null set is defined as a set that contains no elements at all.
Final Answer:
The set A can never be a null set.
The equation ax=1 holds true under certain conditions. Specifically, for any positive a, the equation ax=1 is true if x=0. This is because any non-zero number raised to the power of 0 equals 1.
Since ax=1 when x=0, we can conclude that x=0 is a solution. However, we must consider if there are other solutions.
- If a=1, then 1x=1 for all x. Thus, the set A would contain all real numbers, making it an infinite set.
- If a>1 or 0<a<1, the only solution remains x=0. Thus, the set A would be {0}, which is a singleton set.
From the above analysis, we can conclude:
- If a=1, A is infinite.
- If a≠1, A is a singleton set containing just {0}.
The set A can never be a null set.
Topper's Solved these Questions
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-C(Objective Type Questions(More than one options are correct))
6 Videos
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-D(Linked Comprehension Type Questions))
3 Videos
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-A(Objective Type Questions (One option is correct))
41 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers
11 Videos
- STATISTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason
15 Videos
Similar Questions
Knowledge Check
The set of 3x+24>8x−6,x∈R is......
A{x:−∞<x≤2,x∈R}B{x:−∞≤x<2,x∈R}C{x:−∞≤x≤2,x∈R}D{x:−∞<x<2,x∈R}The solution set of 1≥15−7x>2x−27,x∈N on the number line is
A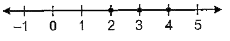 B
B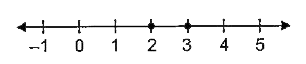 C
C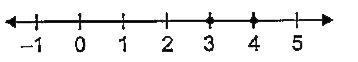 D
D
Let f(x)=tan−1(x2−18x+a)>0x∈R. Then the value of a lies in
View SolutionLet g'(x)>0andf'(x)<0∀x∈R, then
View SolutionIf set A and B are defined as
A={(x,y)∣y=1x,0≠x∈R},B={(x,y)∣y=−x,x∈R,}. Then
View SolutionLet a,b,c∈R with a>0 such that the equation ax2+bcx+b3+c3−4abc=0 has non-real roots.
If P(x)=ax2+bx+candQ(x)=ax2+cx+b, then (a) P(x)>0 for all x∈R and Q(x)<0 for all x∈R. (b) P(x)<0 for all x∈RandQ(x)>0 for all x∈R. (c) neither P(x)>0 for all x∈R nor Q(x)>0 for all x∈R. (d) exactly one of P(x) or Q(x) is positive for all real x.
View SolutionIf set A={1,2,3,4} and a relation R is defined from A to A as follows:
R={(x,y):x>1,y=3}
Find the domain and range of R.
View SolutionLet A={x:x∈R,−1<x<1}, B={x:x∈R,x≤0orx≥2} and A∪B=R−D, then find set D
View Solution
