Illustrate the set {x:−3≤x<0orx>2,x∈R} on a real number line.
To illustrate the set {x:−3≤x<0 or x>2,x∈R} on a real number line, we will follow these steps:
Step 1: Understand the Inequalities
The set consists of two parts:
1. \(-3 \leq x < 0\)
2. \(x > 2\)
Step 2: Draw the Number Line
Begin by drawing a horizontal line to represent the number line. Mark points on this line, including at least the following numbers: \(-3, -2, -1, 0, 1, 2\).
Step 3: Mark the First Interval \((-3, 0)\)
- For the inequality \(-3 \leq x < 0\):
- At \(-3\), we will use a closed circle (or dot) to indicate that \(-3\) is included in the set.
- At \(0\), we will use an open circle to indicate that \(0\) is not included in the set.
- Shade the region between \(-3\) and \(0\) to show that all values in this interval are included.
Step 4: Mark the Second Interval \((2, \infty)\)
- For the inequality \(x > 2\):
- At \(2\), we will use an open circle to indicate that \(2\) is not included in the set.
- Shade the region to the right of \(2\) to indicate that all values greater than \(2\) are included.
Step 5: Combine the Intervals
The final representation on the number line will show the shaded region from \(-3\) to \(0\) (with \(-3\) included and \(0\) excluded) and the shaded region from \(2\) to infinity (with \(2\) excluded).
Final Representation
The number line will look like this:
<---|----|----|----|----|----|----|----|----|----|---->
-4 -3 -2 -1 0 1 2 3 4 5
●=================○ ○================>
Where:
- \(●\) at \(-3\) indicates inclusion.
- \(○\) at \(0\) and \(2\) indicates exclusion.
- The shaded regions represent the values of \(x\) that satisfy the inequalities.
The set consists of two parts:
1. \(-3 \leq x < 0\)
2. \(x > 2\)
Begin by drawing a horizontal line to represent the number line. Mark points on this line, including at least the following numbers: \(-3, -2, -1, 0, 1, 2\).
- For the inequality \(-3 \leq x < 0\):
- At \(-3\), we will use a closed circle (or dot) to indicate that \(-3\) is included in the set.
- At \(0\), we will use an open circle to indicate that \(0\) is not included in the set.
- Shade the region between \(-3\) and \(0\) to show that all values in this interval are included.
- For the inequality \(x > 2\):
- At \(2\), we will use an open circle to indicate that \(2\) is not included in the set.
- Shade the region to the right of \(2\) to indicate that all values greater than \(2\) are included.
The final representation on the number line will show the shaded region from \(-3\) to \(0\) (with \(-3\) included and \(0\) excluded) and the shaded region from \(2\) to infinity (with \(2\) excluded).
The number line will look like this:
<---|----|----|----|----|----|----|----|----|----|---->
-4 -3 -2 -1 0 1 2 3 4 5
●=================○ ○================>
- \(●\) at \(-3\) indicates inclusion.
- \(○\) at \(0\) and \(2\) indicates exclusion.
- The shaded regions represent the values of \(x\) that satisfy the inequalities.
Topper's Solved these Questions
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - QUESTIONS
22 Videos
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Multiple Choice Questions
47 Videos
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions
15 Videos
- HEIGHTS AND DISTANCES BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 C
28 Videos
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(B)
49 Videos
Similar Questions
Knowledge Check
Assertion: The solution set of −1<3+4x≤23,x∈R on the number line is

Reason: In the solution set, the number -1 is not included and the number 5 is included.ABoth assertion and reason are correct and reason is the correct explanation of assertionBBoth assertion and reason are correct but reason is not the correct explanation of assertionCAssertion is correct but reason is incorrectDAssertion is incorrect but reason is correctThe solution set of 3x5+2<x+4≤x2+5,x∈R on the number line is:
A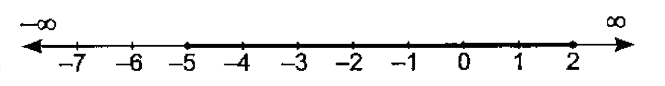 B
B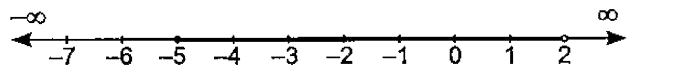 C
C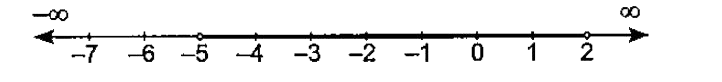 D
D
Assertion: The solution set of 2x−3≤x+1≤4x+7,x∈N is {1, 2, 3,4} .
Reason: If the solution of a linear inequation is x>2,x∈R then on the number line, it is represented as
 ABoth assertion and reason are correct and reason is the correct explanation of assertionBBoth assertion and reason are correct but reason is not the correct explanation of assertionCAssertion is correct but reason is incorrectDAssertion is incorrect but reason is correct
ABoth assertion and reason are correct and reason is the correct explanation of assertionBBoth assertion and reason are correct but reason is not the correct explanation of assertionCAssertion is correct but reason is incorrectDAssertion is incorrect but reason is correct
Given A={x:−1<x≤5,x∈R}andB={x:−4≤x<3,x∈R}.
Represent on different number line :
A - B
View SolutionGive : A={x:−8<5x+2≤17,x∈I}
B={x:−2≤7+3x<17,x∈R}
Where R = {real numbers} and I ={integers}. Represent A and B on two different number lines. Write down the elements of A∩B.
View SolutionGiven P={x:5<2x−1≤11,x∈R} and Q={x:−1≤3+4x<23,x∈I}
where R = {real number } and I = { integers}.
View SolutionSolve the following inequation and write the solution set :
13x−5<15x+4<7x+12,x∈R
Represent the solution on a real number line.
View SolutionThe solution set of 2x+13<3x−25x∈R on the number line is
View Solution
