Two cars A and B move in mutually perpendicular, directions as shown in the figure . Find vBA
(##AAK_T1_PHY_C02_SLV_051_Q01.png" width="80%">
To find the relative velocity vBA of car B with respect to car A, we will follow these steps:
Step 1: Understand the Directions
- Car A is moving in one direction (let's say along the x-axis) with a velocity vA.
- Car B is moving in a direction perpendicular to car A (along the y-axis) with a velocity vB.
Step 2: Write the Relative Velocity Formula
The relative velocity of B with respect to A is given by:
vBA=vB−vA
Since they are moving in perpendicular directions, we can express this in vector form.
Step 3: Represent the Velocities as Vectors
Assume:
- vA=3m/s in the positive x-direction, represented as →vA=3^i.
- vB=4m/s in the positive y-direction, represented as →vB=4^j.
Step 4: Substitute the Values into the Relative Velocity Formula
Substituting the vectors into the relative velocity formula:
vBA=→vB−→vA=4^j−3^i
Step 5: Calculate the Magnitude of vBA
To find the magnitude of vBA:
|vBA|=√(−3)2+(4)2=√9+16=√25=5m/s
Step 6: Determine the Direction of vBA
To find the angle α that vBA makes with the x-axis, we use the tangent function:
tanα=oppositeadjacent=43
Thus,
α=tan−1(43)
Step 7: Calculate the Angle
Using a calculator, we find:
α≈53.13∘
Step 8: Finalize the Direction
Since vBA is in the second quadrant (as car B is moving upwards and car A is moving to the right), the angle with respect to the positive x-axis is:
θ=180∘−53.13∘≈126.87∘
Final Answer
The relative velocity vBA is:
|vBA|=5m/sat an angle of 126.87∘ from the positive x-axis.
---
- Car A is moving in one direction (let's say along the x-axis) with a velocity vA.
- Car B is moving in a direction perpendicular to car A (along the y-axis) with a velocity vB.
The relative velocity of B with respect to A is given by:
vBA=vB−vA
Since they are moving in perpendicular directions, we can express this in vector form.
Assume:
- vA=3m/s in the positive x-direction, represented as →vA=3^i.
- vB=4m/s in the positive y-direction, represented as →vB=4^j.
Substituting the vectors into the relative velocity formula:
vBA=→vB−→vA=4^j−3^i
To find the magnitude of vBA:
|vBA|=√(−3)2+(4)2=√9+16=√25=5m/s
To find the angle α that vBA makes with the x-axis, we use the tangent function:
tanα=oppositeadjacent=43
Thus,
α=tan−1(43)
Using a calculator, we find:
α≈53.13∘
Since vBA is in the second quadrant (as car B is moving upwards and car A is moving to the right), the angle with respect to the positive x-axis is:
θ=180∘−53.13∘≈126.87∘
The relative velocity vBA is:
|vBA|=5m/sat an angle of 126.87∘ from the positive x-axis.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Try yourself
48 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -A Objective (one option is correct)
50 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Two circular coils can be arranged in any of three situations shown in the figure. Their mutual inductance will be (a)
 (b)(##AAK_MCP_32_NEET_PHY_E32_012_Q02.png" width="80%"> (c)
(b)(##AAK_MCP_32_NEET_PHY_E32_012_Q02.png" width="80%"> (c)
View SolutionFind the effective resistance between points A and B for the network shown in the figure below.
(ARH_NEET_PHY_OBJ_V02_C03_S01_027_Q01.png" width="80%">
View Solution
Knowledge Check
What,is the major product ofthe following reaction?
(##BLJ_MSC_OBJ_CHE_JEE_C05B_E01_057_Q01.png" width="80%">A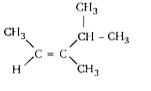 B
B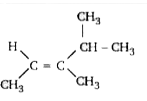 C
C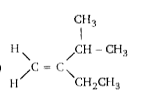 D
D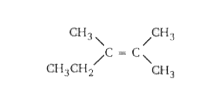
Find the equivalent resistance between P and Q.
(##ARH_NEET_PHY_OBJ_V02_C03_S01_032_Q01.png" width="80%">
View SolutionFrom the following data, show that the decomposition of hydrogen peroxide is a reaction of the first order
(##KALKLCISCCHEXIIC04SLV038_Q01.png width=80%><br>wheretisthetime∈minutesandxisthevolumeofstandardKMnO_4 solution required for titrating the same volume of the reaction mixture.
View SolutionFrom the following data, show that the decomposition of hydrogen peroxide is a reaction of the first order
(##KALKLCISCCHEXIIC04SLV038_Q01.png width=80%><br>wheretisthetime∈minutesandxisthevolumeofstandardKMnO_4 solution required for titrating the same volume of the reaction mixture.
View SolutionFrom the following data, show that the decomposition of hydrogen peroxide is a reaction of the first order
(##KALKLCISCCHEXIIC04SLV038_Q01.png width=80%><br>wheretisthetime∈minutesandxisthevolumeofstandardKMnO_4 solution required for titrating the same volume of the reaction mixture.
View SolutionFig. shows a light (blue + red + green) incident on a prism and on a parallel sided glass slab. Complete the diagrams by drawing the refracted and the emergent rays.
(##SEL_RPG_ICSE_PHY_X_C06_SLV_001_Q01.png" width="80%">
View SolutionA ball of radius r and density ρ falls freely under gravity through a distance h before entering water. Velocity of ball does not change even on entering water. If viscosity of water is η the value of h is given by
(##DPP_PHY_CP09_E01_002_Q01.png" width="80%">
View SolutionCalculate the angles x,y and z if
x3=y4=z5
(##SEL_RKB_ICSE_MAT_X_C17_E02_042_Q01.png" width="80%">
View Solution
