A particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
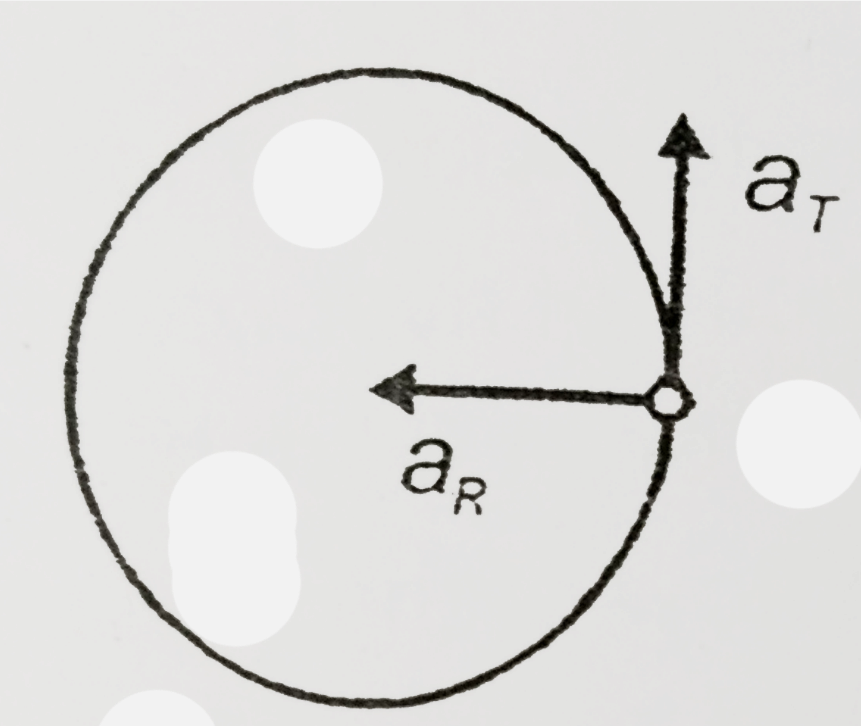
The magnitude of tangential acceleration at t=R2u is
a. R
2R
2πR
πR
The correct Answer is:A
Step by step video solution for A particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u. The magnitude of tangential acceleration at t = R/(2u) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -E (Assertion-Reason)
4 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -F (Matrix-Match)
2 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -C Objective (More than one option is correct)
7 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
A particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
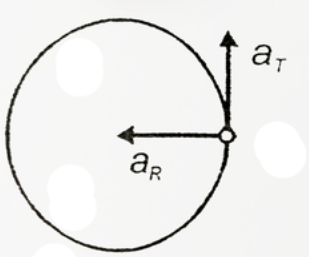
The time after which the speed of particle reduces to half of its initial value is
View SolutionA particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals v0, then th speed of the particle as a function of the distance covered S will be
View SolutionAt freezing point of a solution there is always
View SolutionA particle is moving on a circle of radius R such that at every instant the tangential and radial accelerations are equal in magnitude. If the velocity of the particle be v0 at t=0, the time for the completion of the half of the first revolution will be
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionA particle is moving on a circle of radius A .At an instant its speed and tangential acceleration are B and C respectively.Total acceleration of the particle at that instant is
View SolutionA particle with the constant speed in a circle of radius r and time period T.The centripetal acceleration of a particle is
View Solution
