A particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is
1/α
√α
1/√α
α
The correct Answer is:C
To solve the problem of finding the time at which the magnitudes of tangential and radial acceleration are equal for a particle moving in a circular path with constant angular acceleration, we can follow these steps:
1. Understand the Definitions:
- Tangential acceleration (At) is given by the formula:
At=α⋅r
where α is the angular acceleration and r is the radius of the circular path.
- Radial (centripetal) acceleration (Ar) is given by the formula:
Ar=ω2⋅r
where ω is the angular velocity.
2. Set the Accelerations Equal:
- We need to find the time when the magnitudes of tangential and radial acceleration are equal:
At=Ar
- Substituting the expressions for At and Ar:
α⋅r=ω2⋅r
- Since r is common on both sides, we can divide by r (assuming r≠0):
α=ω2
3. Relate Angular Velocity to Time:
- We know that the angular velocity ω can be expressed in terms of angular acceleration and time using the equation of motion:
ω=ω0+αt
- Given that the initial angular velocity ω0=0 (the particle starts from rest):
ω=αt
4. Substitute ω in the Equation:
- From the previous step, we have ω=αt. Substitute this into the equation α=ω2:
α=(αt)2
- This simplifies to:
α=α2t2
5. Solve for Time t:
- Dividing both sides by α (assuming α≠0):
1=αt2
- Rearranging gives:
t2=1α
- Taking the square root of both sides:
t=1√α
6. Conclusion:
- The time at which the magnitudes of tangential and radial acceleration are equal is:
t=1√α
Final Answer:
The time at which the magnitudes of tangential and radial acceleration are equal is t=1√α.
- Tangential acceleration (At) is given by the formula:
At=α⋅r
where α is the angular acceleration and r is the radius of the circular path.
- Radial (centripetal) acceleration (Ar) is given by the formula:
Ar=ω2⋅r
where ω is the angular velocity.
- We need to find the time when the magnitudes of tangential and radial acceleration are equal:
At=Ar
- Substituting the expressions for At and Ar:
α⋅r=ω2⋅r
- Since r is common on both sides, we can divide by r (assuming r≠0):
α=ω2
- We know that the angular velocity ω can be expressed in terms of angular acceleration and time using the equation of motion:
ω=ω0+αt
- Given that the initial angular velocity ω0=0 (the particle starts from rest):
ω=αt
- From the previous step, we have ω=αt. Substitute this into the equation α=ω2:
α=(αt)2
- This simplifies to:
α=α2t2
- Dividing both sides by α (assuming α≠0):
1=αt2
- Rearranging gives:
t2=1α
- Taking the square root of both sides:
t=1√α
- The time at which the magnitudes of tangential and radial acceleration are equal is:
t=1√α
The time at which the magnitudes of tangential and radial acceleration are equal is t=1√α.
Topper's Solved these Questions
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Main (Archive)
19 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Advanced (Archive)
19 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - Long Answer Type
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
Similar Questions
A particle is moving with a constant angular acceleration of 4rad/s2 in a circular path. At time t=0 , particle was at rest. Find the time at which the magnitudes of centripetal acceleration and tangential acceleration are equal.
View SolutionA particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V0. Find the speed of the particle after time t=(R)/(2V0)
View Solution
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
A point mass moves along a circle of radius R with a constant angular acceleration α. How much time is needed after motion begins for the radial acceleration of the point mass to be equal to its tangential acceleration ?
View SolutionA particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionA ball starts moving in a circular slot with angular acceleration α=2rad/s2 at t=0 The angle between its velocity and acceleration varies with time as
View SolutionA point starts from rest and moves along a circular path with a constant tangential acceleration. After one rotation, the ratio of its radial acceleration to its tangential acceleration will be equal to
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
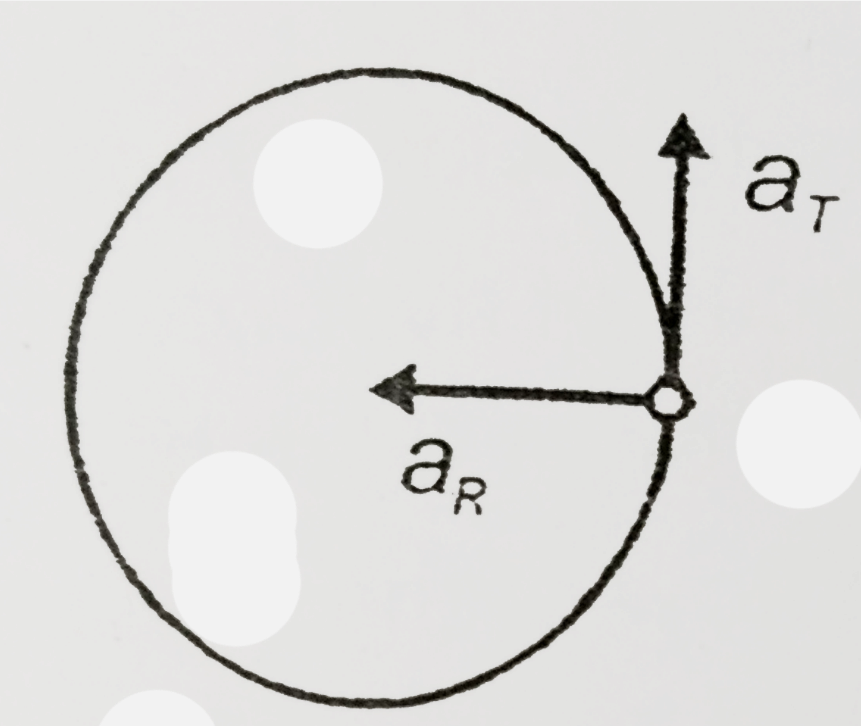
The magnitude of tangential acceleration at t=R2u is
View SolutionA disc rotates about its axis with a constant angular acceleration of 4rads2. Find the radial and tangential acceleration of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
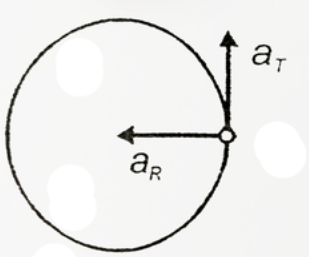
The time after which the speed of particle reduces to half of its initial value is
View Solution
