A magnet is allowed to fall towards a metal ring. During the fall Its accelertion is
Equal to g
Greater than g
Less than g
Equal to the product of g and the radius of the ring
The correct Answer is:C
To solve the problem of a magnet falling towards a metal ring, we need to analyze the forces acting on the magnet and the effects of electromagnetic induction. Here’s a step-by-step solution:
Step 1: Understanding the Setup
When a magnet is allowed to fall towards a metal ring, it moves through a magnetic field. The magnet has a north and south pole, and as it approaches the ring, the magnetic flux through the area enclosed by the ring changes.
Hint: Remember that a changing magnetic flux induces an electromotive force (EMF) in the conductor (the metal ring).
Step 2: Applying Faraday's Law of Induction
According to Faraday's law, a change in magnetic flux through a circuit induces an electromotive force (EMF) in that circuit. As the magnet falls, the magnetic flux through the ring increases, which induces a current in the ring.
Hint: Consider how the direction of the induced current is determined by Lenz's law.
Step 3: Lenz's Law
Lenz's law states that the direction of the induced current will be such that it opposes the change in magnetic flux. In this case, as the magnet falls and the flux increases downward, the induced current will create a magnetic field that opposes this increase. Therefore, the induced magnetic field will have its north pole facing upward, repelling the north pole of the falling magnet.
Hint: Think about how the interaction between the induced magnetic field and the falling magnet affects the motion of the magnet.
Step 4: Analyzing Forces on the Magnet
The forces acting on the falling magnet include:
- The gravitational force (weight) acting downward, mg.
- The magnetic repulsive force from the induced current in the ring acting upward.
Let F be the magnetic force acting upward due to the induced current. The net force acting on the magnet can be expressed as:
Fnet=mg−F
Hint: Remember that the net force affects the acceleration of the magnet.
Step 5: Applying Newton's Second Law
According to Newton's second law, the net force is also equal to the mass of the magnet times its acceleration a:
Fnet=ma
Setting the two expressions for net force equal gives:
ma=mg−F
From this, we can solve for acceleration a:
a=g−Fm
Hint: Consider how the magnitude of the magnetic force F affects the acceleration of the magnet.
Step 6: Conclusion on Acceleration
Since the magnetic force F is always positive and acts upward, it reduces the effective acceleration of the magnet. Therefore, the acceleration a of the magnet is less than g:
a<g
Thus, the final conclusion is that the acceleration of the magnet as it falls towards the metal ring is less than the acceleration due to gravity.
Final Answer: The acceleration of the magnet during its fall is less than g.
When a magnet is allowed to fall towards a metal ring, it moves through a magnetic field. The magnet has a north and south pole, and as it approaches the ring, the magnetic flux through the area enclosed by the ring changes.
According to Faraday's law, a change in magnetic flux through a circuit induces an electromotive force (EMF) in that circuit. As the magnet falls, the magnetic flux through the ring increases, which induces a current in the ring.
Lenz's law states that the direction of the induced current will be such that it opposes the change in magnetic flux. In this case, as the magnet falls and the flux increases downward, the induced current will create a magnetic field that opposes this increase. Therefore, the induced magnetic field will have its north pole facing upward, repelling the north pole of the falling magnet.
The forces acting on the falling magnet include:
- The gravitational force (weight) acting downward, mg.
- The magnetic repulsive force from the induced current in the ring acting upward.
Fnet=mg−F
According to Newton's second law, the net force is also equal to the mass of the magnet times its acceleration a:
Fnet=ma
ma=mg−F
From this, we can solve for acceleration a:
a=g−Fm
Since the magnetic force F is always positive and acts upward, it reduces the effective acceleration of the magnet. Therefore, the acceleration a of the magnet is less than g:
a<g
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - B)
22 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - C)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Try Yourself
42 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A metallic ring with a small cut is held horizontally and a magnet is allowed to fall vertically through the ring then the acceleration of the magnet is :
View SolutionA resistance coil is held horizontally and a magnet is allowed to fall vertically through it . Then the acceleration of the magnet while passing through the coil is
View SolutionA short magnet is allowed to fall from rest along the axis of a horizontal conducting ring. The distance fallen by the magnet in one second may be
View SolutionA body of mass m is allowed to fall with the help of string with downward acceleration g6 to a distance x. The work done by the string is
View SolutionA small magnet M is allowed to fall through a fixed horizontal conducting ring R. Let g be the acceleration due to gravity. The acceleration of M will be
View SolutionA bar magnet is dropped along the axis of copper ring held horizontally. The acceleration of fall is
View SolutionIf light of wavelength λ1 is allowed to fall on a metal , then kinetic energy of photoelectrons emitted is E1. If wavelength of light changes to λ2 then kinetic energy of electrons changes to E2. Then work function of the metal is
View SolutionA ball falls towards the earth. Which of the following is correct?
View SolutionThe North pole of a magnet is falling on a metallic ring as shown in the figure. The direction of induced current, if looked from upside in the ring will be
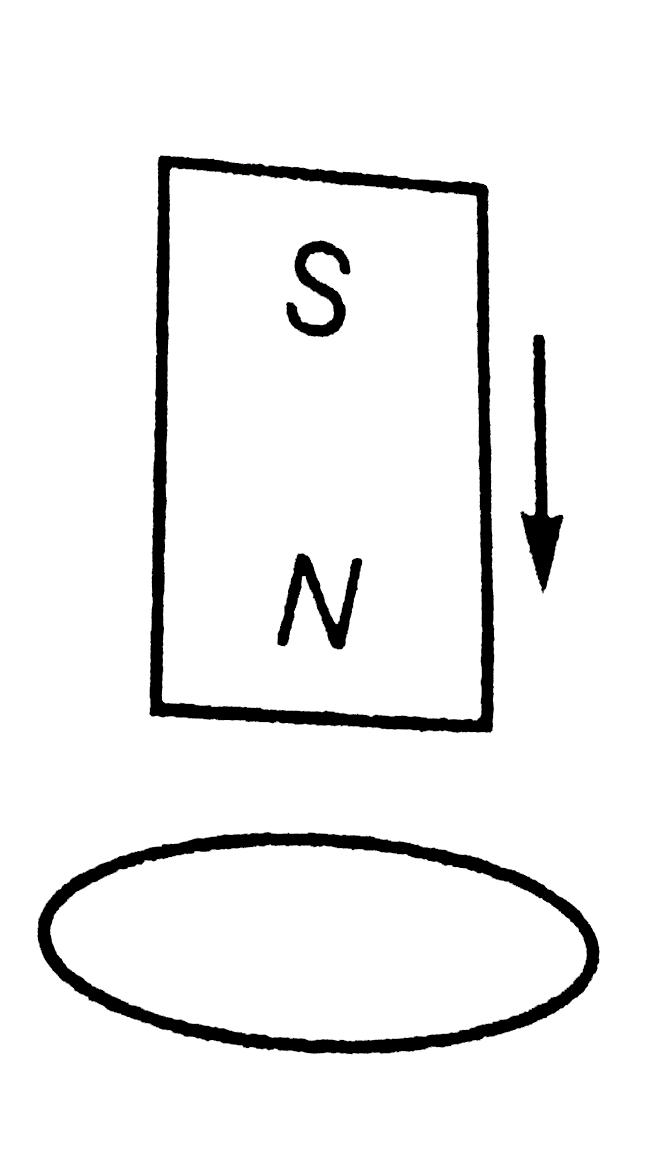
View SolutionA copper ring is suspended by a thread. One end of a magnet is brought horizontally towards the ring. How. Will it affect the position of the ring?
View Solution
