Suppose that you are given a system of two equations of the following form
Acosϕ=Bv1−Bv2cosθ…………..(1)
Asinϕ=Bv2sinθ………..(2)
Show that,
A2=B2(v21+v22−2v1v2cosθ)
To solve the given problem, we will manipulate the two equations step by step to arrive at the desired result.
Given equations:
1. Acosϕ=Bv1−Bv2cosθ (Equation 1)
2. Asinϕ=Bv2sinθ (Equation 2)
Step 1: Square both equations.
Starting with Equation 1:
(Acosϕ)2=(Bv1−Bv2cosθ)2
This expands to:
A2cos2ϕ=B2v21−2B2v1v2cosθ+B2v22cos2θ(3)
Now for Equation 2:
(Asinϕ)2=(Bv2sinθ)2
This expands to:
A2sin2ϕ=B2v22sin2θ(4)
Step 2: Add the two squared equations.
Adding equations (3) and (4):
A2cos2ϕ+A2sin2ϕ=B2v21−2B2v1v2cosθ+B2v22cos2θ+B2v22sin2θ
Step 3: Simplify the left side using the Pythagorean identity.
Using the identity cos2ϕ+sin2ϕ=1:
A2(cos2ϕ+sin2ϕ)=A2⋅1=A2
Step 4: Simplify the right side.
On the right side, we can factor out B2:
A2=B2(v21−2v1v2cosθ+v22(cos2θ+sin2θ))
Using cos2θ+sin2θ=1:
A2=B2(v21−2v1v2cosθ+v22)
Step 5: Rearranging the right side.
The expression simplifies to:
A2=B2(v21+v22−2v1v2cosθ)
Final Result:
Thus, we have shown that:
A2=B2(v21+v22−2v1v2cosθ)
This completes the proof.
---
1. Acosϕ=Bv1−Bv2cosθ (Equation 1)
2. Asinϕ=Bv2sinθ (Equation 2)
(Acosϕ)2=(Bv1−Bv2cosθ)2
This expands to:
A2cos2ϕ=B2v21−2B2v1v2cosθ+B2v22cos2θ(3)
(Asinϕ)2=(Bv2sinθ)2
This expands to:
A2sin2ϕ=B2v22sin2θ(4)
A2cos2ϕ+A2sin2ϕ=B2v21−2B2v1v2cosθ+B2v22cos2θ+B2v22sin2θ
A2(cos2ϕ+sin2ϕ)=A2⋅1=A2
A2=B2(v21−2v1v2cosθ+v22(cos2θ+sin2θ))
Using cos2θ+sin2θ=1:
A2=B2(v21−2v1v2cosθ+v22)
A2=B2(v21+v22−2v1v2cosθ)
Thus, we have shown that:
A2=B2(v21+v22−2v1v2cosθ)
This completes the proof.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Try Yourself32videos
TRIGNOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Assignment section-A (Objective Type Questions (One option is correct))49videos
TRIGNOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J10videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - SECTION-J (Aakash Challengers Questions)5videos
VECTOR ALGEBRA
Similar Questions
Solve the following equation: sin2θ−cosθ=14
View SolutionTwo particles of equal mass in are projected from the ground with speeds v1 and v2 at angles θ1, and θ2 as shown in the figure. Given θ2>θ1 and v1cosθ1=v2cosθ2Which statement/s is/are correct?
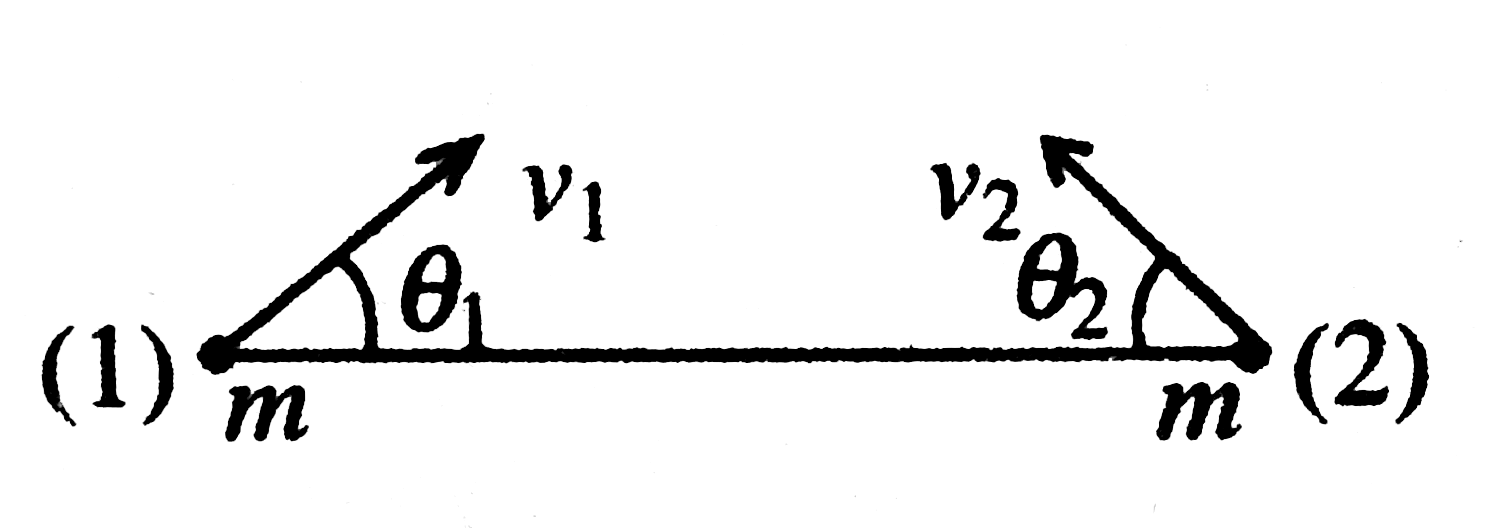 View Solution
View SolutionThe possible value of θ∈[−π,π] satisfying the equation 2(cosθ+cos2θ)+(1+2cosθ)sin2θ=2sinθ are
View SolutionSolve the following system of equations: 15u+2v=17, 1u+1v=365
View Solutionsinθ1+cosθ+1+cosθsinθ=2cosecθ
View SolutionifA=[cosθsinθ−sinθcosθ], then show that : A2=[cos2θsin2θ−sin2θcos2θ]
View SolutionProve the following identity: 2sinθcosθ−cosθ1−sinθ+sin2θ−cos2θ=cotθ
View SolutionProve the following trigonometric identities : (1+cot2θ)(1−cosθ)(1+cosθ)=1 (ii) tan2θ−1cos2θ=−1
View SolutionFind the general values of θ which satisfy the following equations:
i) sinθ=1√2 , ii) cosθ=12 , (iii) tanθ=√3, iv) cotθ=1 , v) secθ=2√3, vi) cosecθ=√2View SolutionIf cosθ=12(a+1a), show that cos2θ=12⋅(a2+1a2)
View Solution

