In a triangle the length of the two larger sides are 24 and 22, respectively.If the angles are in A.P.,then the third side ,is
12+2√13
12−3√2
2√3+2
2√3−2
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Define the Angles
Let the angles of the triangle be A, B, and C. Since the angles are in Arithmetic Progression (A.P.), we can express them as:
- A=B−d
- B=B
- C=B+d
Step 2: Use the Sum of Angles in a Triangle
The sum of the angles in a triangle is 180∘:
A+B+C=180∘
Substituting the expressions for A and C:
(B−d)+B+(B+d)=180∘
This simplifies to:
3B=180∘⟹B=60∘
Step 3: Find Angles A and C
Now, substituting B back into the expressions for A and C:
A=60∘−d
C=60∘+d
Step 4: Use the Law of Cosines
We know the lengths of two sides of the triangle:
- a=24 (opposite angle A)
- b=22 (opposite angle B)
Using the Law of Cosines:
c2=a2+b2−2abcos(B)
Substituting the known values:
c2=242+222−2⋅24⋅22⋅cos(60∘)
Since cos(60∘)=12:
c2=576+484−2⋅24⋅22⋅12
c2=576+484−24⋅22
Calculating 24⋅22:
24⋅22=528
So,
c2=576+484−528
c2=532
Step 5: Solve for c
Now, we take the square root to find c:
c=√532=√4⋅133=2√133
Step 6: Approximate the Value
To find the approximate value of c:
c≈2√133≈2⋅11.53≈23.06
Conclusion
Thus, the third side c can be expressed as:
c=12+2√13
This matches with option 1.
Let the angles of the triangle be A, B, and C. Since the angles are in Arithmetic Progression (A.P.), we can express them as:
- A=B−d
- B=B
- C=B+d
The sum of the angles in a triangle is 180∘:
A+B+C=180∘
Substituting the expressions for A and C:
(B−d)+B+(B+d)=180∘
This simplifies to:
3B=180∘⟹B=60∘
Now, substituting B back into the expressions for A and C:
A=60∘−d
C=60∘+d
We know the lengths of two sides of the triangle:
- a=24 (opposite angle A)
- b=22 (opposite angle B)
c2=a2+b2−2abcos(B)
Substituting the known values:
c2=242+222−2⋅24⋅22⋅cos(60∘)
Since cos(60∘)=12:
c2=576+484−2⋅24⋅22⋅12
c2=576+484−24⋅22
Calculating 24⋅22:
24⋅22=528
So,
c2=576+484−528
c2=532
Now, we take the square root to find c:
c=√532=√4⋅133=2√133
To find the approximate value of c:
c≈2√133≈2⋅11.53≈23.06
Thus, the third side c can be expressed as:
c=12+2√13
This matches with option 1.
Topper's Solved these Questions
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section-C (Objective Type Questions More than one options are correct )
45 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section D (Linked Comprehension Type Questions)
27 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Assignment Section-B (Objective Type Questions (One option is correct))
1 Video
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J
10 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - SECTION-J (Aakash Challengers Questions)
5 Videos
Similar Questions
In a triangle, the lengths of the two larger sides are 10 and 9, respectively. If the angles are in A.P., then the length of the third side can be 5−√6 (b) 3√3 (c) 5 (d) 5+√6
View SolutionIn a triangle, the lengths of the two larger sides are 10 and 9, respectively. If the angles are in A.P, then the length of the third side can be (a) 5−√6 (b) 3√3 (c) 5 (d) 5+√6
View SolutionFind the length of the third side of the triangle.
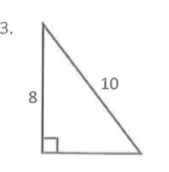
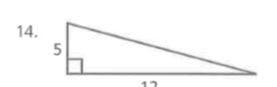
View SolutionFind the length of the third side of the triangle.
View SolutionThe sides of a right angled triangle arein A.P., then they are in the ratio
View SolutionThe areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26cm, what is the length of the longest side of the smaller triangle?
View SolutionThe areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
View SolutionIf the length of sides of right angled triangle are in AP, then their ratio is
View SolutionIf the cotangents of half the angles of a triangle are in A.P., then prove that the sides are in A.P.
View SolutionTwo sides of a triangle are of lengths √6and4 and the angle opposite to smaller side is 30. How many such triangles are possible? Find the length of their third side and area.
View Solution
