In a triangle ABC, if the median and altitude from A trisect angle A, then (B−C) is (in degrees) equal to………. a) 0 degree b) 30 degree c) 60 degree d) 90 degree
0 degree
30 degree
60 degree
90 degree
To solve the problem, we need to analyze the triangle ABC where the median and altitude from vertex A trisect angle A. Let's denote the angles as follows:
- Let angle A = 3A (since it is trisected into three equal parts).
- Therefore, angle BAD = angle DAM = angle MAC = A.
1. Construct Triangle ABC:
- Draw triangle ABC with vertex A at the top.
- Let D be the foot of the altitude from A to side BC, and let M be the midpoint of BC (the point where the median from A intersects BC).
2. Identify Angles:
- Since AD is the altitude, angle ADB = angle ADC = 90 degrees.
- Since AM is the median, BM = CM.
3. Trisecting Angle A:
- Since angle A is trisected, we have:
- angle BAD = angle DAM = angle MAC = A.
- Therefore, angle A = 3A.
4. Using Congruent Triangles:
- In triangles ABD and AMD:
- angle BAD = angle DAM = A,
- angle ADB = angle ADM = 90 degrees,
- AD is common.
- By the criteria of congruence (Angle-Angle-Side), triangles ABD and AMD are congruent.
- Thus, BD = DM.
5. Finding Relationships:
- Since BM = CM, we have DM = 1/2 CM.
- This implies that BD = 1/2 CM.
6. Using the Angle Bisector Theorem:
- In triangle ADC, since AM is the angle bisector:
- By the Angle Bisector Theorem, we have:
ADDC=DMCM=12
- This means AD = 1/2 DC.
7. Using Trigonometric Ratios:
- In triangle ADC, we know angle DAC = 2A (since angle A = 3A).
- Using the cosine ratio:
cosC=ADAC
- Since AD = 1/2 DC, we can find that:
cosC=12
- This implies angle C = 60 degrees.
8. Finding Angle A:
- Since angle DAC = 2A and we know angle C = 60 degrees:
2A=60⇒A=30 degrees
9. Finding Angles B and C:
- The sum of angles in triangle ABC gives:
A+B+C=180⇒30+B+60=180
- Therefore, angle B = 90 degrees.
10. Calculating B - C:
- Finally, we find:
B−C=90−60=30 degrees
Conclusion:
Thus, the value of B−C is 30 degrees.
- Therefore, angle BAD = angle DAM = angle MAC = A.
- Draw triangle ABC with vertex A at the top.
- Let D be the foot of the altitude from A to side BC, and let M be the midpoint of BC (the point where the median from A intersects BC).
- Since AD is the altitude, angle ADB = angle ADC = 90 degrees.
- Since AM is the median, BM = CM.
- Since angle A is trisected, we have:
- angle BAD = angle DAM = angle MAC = A.
- Therefore, angle A = 3A.
- In triangles ABD and AMD:
- angle BAD = angle DAM = A,
- angle ADB = angle ADM = 90 degrees,
- AD is common.
- By the criteria of congruence (Angle-Angle-Side), triangles ABD and AMD are congruent.
- Thus, BD = DM.
- Since BM = CM, we have DM = 1/2 CM.
- This implies that BD = 1/2 CM.
- In triangle ADC, since AM is the angle bisector:
- By the Angle Bisector Theorem, we have:
ADDC=DMCM=12
- This means AD = 1/2 DC.
- In triangle ADC, we know angle DAC = 2A (since angle A = 3A).
- Using the cosine ratio:
cosC=ADAC
- Since AD = 1/2 DC, we can find that:
cosC=12
- This implies angle C = 60 degrees.
- Since angle DAC = 2A and we know angle C = 60 degrees:
2A=60⇒A=30 degrees
- The sum of angles in triangle ABC gives:
A+B+C=180⇒30+B+60=180
- Therefore, angle B = 90 degrees.
- Finally, we find:
B−C=90−60=30 degrees
Thus, the value of B−C is 30 degrees.
Topper's Solved these Questions
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
16 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section -H (Multiple True-false, type Questions)
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J
10 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - SECTION-J (Aakash Challengers Questions)
5 Videos
Similar Questions
Knowledge Check
In this triangle, what is the degree measure of angle c ?
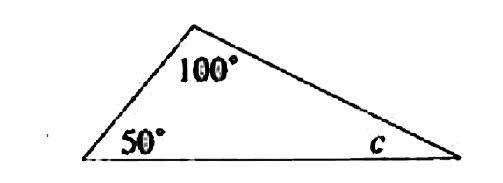 A17B20C30D40
A17B20C30D40To increase the length of brass rod by 2% its temperature should increase by (α=0.00002∘C−1) a) 800 degree C b) 900 degree C c) 1000 degree C d) 1100 degree C
A800∘CB900∘CC1000∘CD1100∘CThere is some change in length when a 33000N tensile force is applied on a steel rod of area of cross-section 10−3m2. The change in temperature of the steel rod when heated is
(Y=3×1011N/m2,α=1.1×10−5/∘C) a) 20 degree C b) 15 degree C c) 10 degree C d) 0 degree CA20∘CB15∘CC10∘CD0∘C
If two acute angles of a right triangle are equal, then each acute is equal to (a)300 (b) 450 (c) 600 (d) 900
View SolutionThe angles in a triangle are in A.P. and the ratio of the smallest angle in degrees to the greatest angle in radians is 60:ϕ Find the angle of the triangle in degrees and radians.
View Solution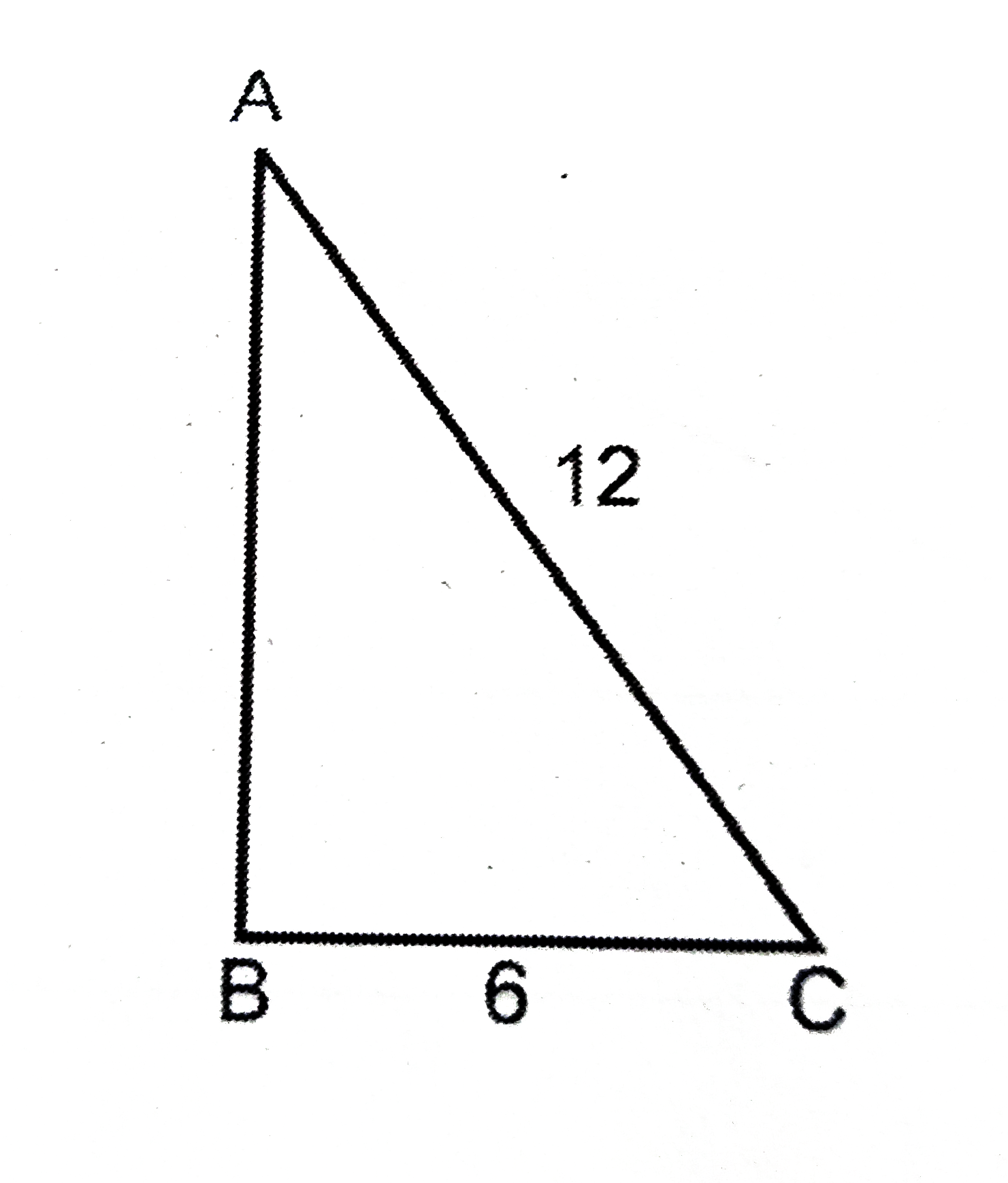
In the figure shown above, ABC is a triangle right angled at B. What is the value of angle A, in degrees?
View SolutionThe differential equation of all parabolas each of which has a latus rectum 4a and whose axes are parallel to the x-axis is (a) of order 1 and degree 2 (b) of order 2 and degree 3 (c) of order 2 and degree 1 (d) of order 2 and degree 2
View SolutionAn angle of 30 radians is equal to how many degrees?
View Solution
