The radius of the circle touching two sides AB and AC of a triangle ABC and having its center on BC is equal to………………..
To find the radius of the circle that touches two sides AB and AC of triangle ABC and has its center on side BC, we can follow these steps:
1. Understanding the Problem: We need to find the radius R of a circle that touches the sides AB and AC of triangle ABC and has its center on side BC.
2. Label the Triangle: Let A be the vertex opposite side BC, B be the vertex opposite side AC, and C be the vertex opposite side AB. Let the lengths of sides BC, AC, and AB be a, b, and c respectively.
3. Identify the Areas: The area of triangle ABC can be denoted as Δ. The area can also be expressed using the formula:
Δ=12×base×height
For triangle AOB (where O is the center of the circle), the area is:
Area of AOB=12×c×R
For triangle AOC:
Area of AOC=12×b×R
4. Total Area of Triangle ABC: The total area of triangle ABC can be expressed as the sum of the areas of triangles AOB and AOC:
Δ=Area of AOB+Area of AOC=12cR+12bR
This simplifies to:
Δ=12R(b+c)
5. Expressing R in Terms of Area: Rearranging the equation gives:
R=2Δb+c
6. Final Result: Thus, the radius R of the circle that touches sides AB and AC and has its center on side BC is given by:
R=2Δb+c
Δ=12×base×height
For triangle AOB (where O is the center of the circle), the area is:
Area of AOB=12×c×R
For triangle AOC:
Area of AOC=12×b×R
Δ=Area of AOB+Area of AOC=12cR+12bR
This simplifies to:
Δ=12R(b+c)
R=2Δb+c
R=2Δb+c
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)16videos
TRIGNOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section -H (Multiple True-false, type Questions)9videos
TRIGNOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J10videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - SECTION-J (Aakash Challengers Questions)5videos
VECTOR ALGEBRA
Similar Questions
In ΔABC,∠A=π3 and its incircle of unit radius. Find the radius of the circle touching the sides AB, AC internally and the incircle of ΔABC externally is x , then the value of x is
View SolutionIf the radius of the circumcircle of the isosceles triangle ABC is equal to AB(=AC), then the angle A is equal to-
View SolutionLet ABC be a triangle and a circle C1 drawn lying inside the triangle touching its incircle C2 externally and also touching its two sides AB and AC. Show that the ratio of radii of the circles C1 and C2 is equal to tan2(π−A4)
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A <br>If ∠GAC=π3anda=3b, then sin C is equal to
View SolutionA circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right-angled triangle whose radius of the circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. Area of Δ ABC is
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If BC=6,AC=8, then the length of side AB is equal toView SolutionA circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
Does the perpendicular bisector of BC pass through O?View SolutionFind the radius of the circle escribed to the triangle ABC (Shown in the figure below) on the side BC if ∠NAB=30∘,∠BAC=30∘,AB=AC=5.
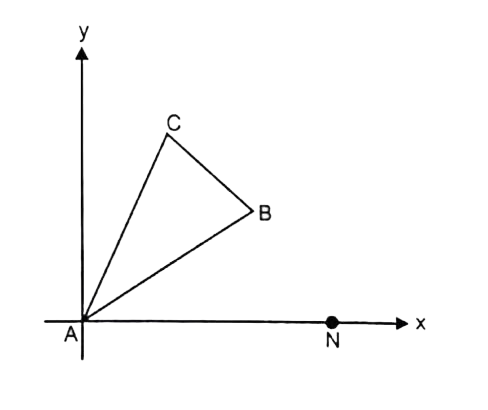 View Solution
View SolutionFind the radius of the circle escribed to the triangle ABC (Shown in the figure below) on the side BC if ∠NAB=30∘,∠BAC=30∘, AB=AC=5.
 View Solution
View Solution

