Given A = {p, q}. List all the relations on A.
To find all the relations on the set A={p,q}, we can follow these steps:
Step 1: Determine the Cartesian Product A×A
First, we need to find the Cartesian product of set A with itself, which is denoted as A×A. The Cartesian product consists of all ordered pairs where the first element is from the first set and the second element is from the second set.
A×A={(p,p),(p,q),(q,p),(q,q)}
Step 2: Count the Total Number of Relations
The total number of relations on a set is given by 2n, where n is the number of elements in the Cartesian product. In our case, since A×A has 4 elements, we calculate:
Total Relations=24=16
Step 3: List All Possible Relations
Now we will list all possible subsets of A×A. Each subset represents a different relation. The subsets can include:
1. ∅ (the empty relation)
2. {(p,p)}
3. {(p,q)}
4. {(q,p)}
5. {(q,q)}
6. {(p,p),(p,q)}
7. {(p,p),(q,p)}
8. {(p,p),(q,q)}
9. {(p,q),(q,p)}
10. {(p,q),(q,q)}
11. {(q,p),(q,q)}
12. {(p,p),(p,q),(q,p)}
13. {(p,p),(p,q),(q,q)}
14. {(p,p),(q,p),(q,q)}
15. {(p,q),(q,p),(q,q)}
16. {(p,p),(p,q),(q,p),(q,q)}
Conclusion
Thus, the total number of relations on the set A={p,q} is 16, and we have listed all possible relations.
---
2. {(p,p)}
3. {(p,q)}
4. {(q,p)}
5. {(q,q)}
6. {(p,p),(p,q)}
7. {(p,p),(q,p)}
8. {(p,p),(q,q)}
9. {(p,q),(q,p)}
10. {(p,q),(q,q)}
11. {(q,p),(q,q)}
12. {(p,p),(p,q),(q,p)}
13. {(p,p),(p,q),(q,q)}
14. {(p,p),(q,p),(q,q)}
15. {(p,q),(q,p),(q,q)}
16. {(p,p),(p,q),(q,p),(q,q)}
Topper's Solved these Questions
- RELATIONS AND FUNCTIONS Book:AAKASH INSTITUTE ENGLISHChapter:RELATIONS AND FUNCTIONS Exercise:Assignment (Section - A) Objective Type Questions (one option is correct)
Explore 102 Videos
- RELATIONS AND FUNCTIONS Book:AAKASH INSTITUTE ENGLISHChapter:RELATIONS AND FUNCTIONS Exercise:Assignment (Section - B) Objective Type Questions (one option is correct)
Explore 86 Videos
- RELATIONS AND FUNCTIONS Book:AAKASH INSTITUTE ENGLISHChapter:RELATIONS AND FUNCTIONS Exercise:Assignment (Section - J) Aakash Challengers Questions
Explore 8 Videos
- PROBABILITYBook:AAKASH INSTITUTE ENGLISHChapter:PROBABILITYExercise:ASSIGNMENT SECTION-J (aakash challengers questions)
Explore 11 Videos
- SEQUENCES AND SERIES Book:AAKASH INSTITUTE ENGLISHChapter:SEQUENCES AND SERIES Exercise:Assignment (SECTION - J) Aakash Challengers
Explore 11 Videos
Similar Questions
Knowledge Check
Let n(A)=p. Then the number of all relations on A is
A2pB2p!C2p2DNone of these
Let A={a,b} . List all relations on A and find their number.
View SolutionGiven A={2,3,4,5,6}. List the elements of each of the following relations:
{(x,y)∈A×A:x=y}
View SolutionLet A={p,q,r}. Which of the following is an equivalence relation on A?
(i) R={(p,q),(q,r),(p,r),(p,p)}
(ii) R={(p,p),(q,q),(r,r),(q,p)}
(iii) R={(p,p),(q,q),(r,r)}
(iv) R={(p,p),(q,q),(r,r),(p,q),(q,r),(p,r)}
(v) R={(p,p),(q,q),(r,r),(p,q),(q,p)}
View SolutionLet O be the origin. We define a relation between two points P and Q in a plane if OP=OQ . Show that the relation, so defined is an equivalence relation.
View SolutionLet A={p,q,r}. Which of the following is an equivalence relation on A? (a) R1={(p,q),(q,r),(p,r),(p,q)} (b) R2={(r,q),(r,p),(r.r),(q,r)} (c) R3={(p,p),(q,q),(r,r),(p,q)} (d) one of these
View Solution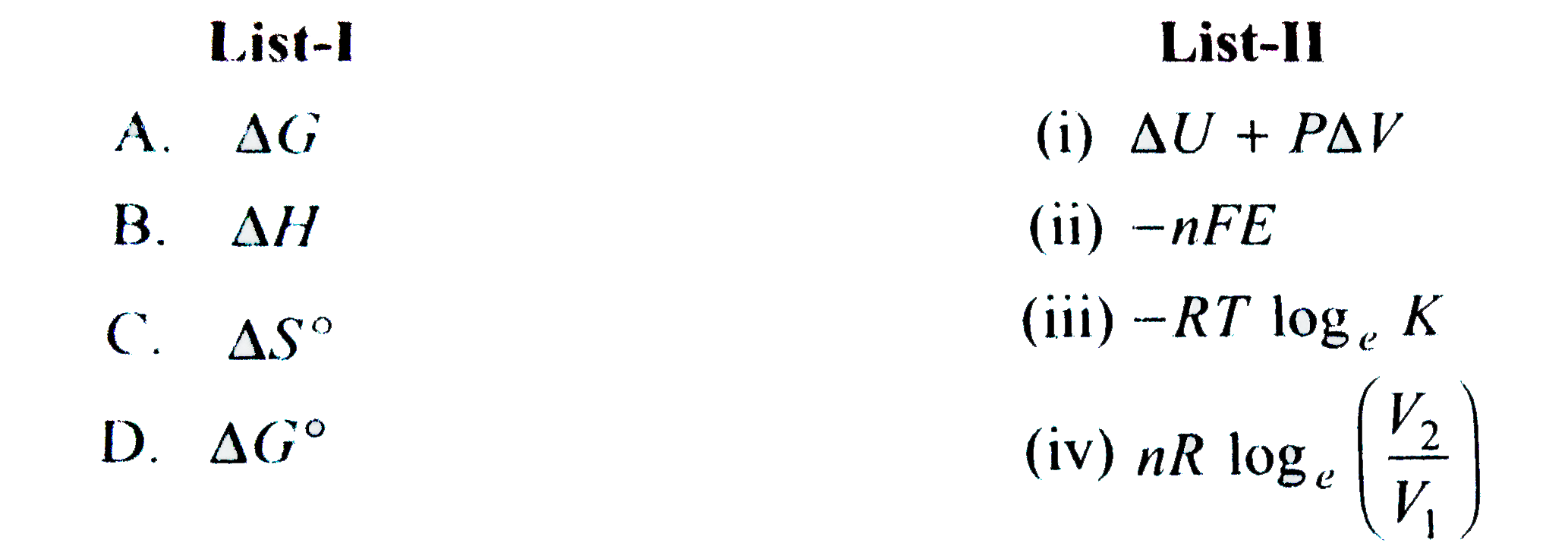 ltBrgt Match the physical changes in List-I with their relations given in List-II:
ltBrgt Match the physical changes in List-I with their relations given in List-II:
View SolutionLet O be the origin. We define a relation between two points P and Q in a plane if OP=OQ. Show that the relation, so defined is an equivalence relation.
View Solution