Which of the following can be the valid assignment of probability for outcomes of sample space, S={W1,W2,W3},{ where W1,W2 and W3 are mutually exclusive events
Assignment
w1w2w3(a)0.40.20.8(b)001(c)−123412(d)121214
To determine which of the given assignments of probability for the outcomes of the sample space S={W1,W2,W3} is valid, we need to check each option against the following conditions:
1. The sum of the probabilities must equal 1.
2. Each probability must be non-negative.
Let's analyze each option step by step.
Step 1: Check Option A
Probabilities: P(W1)=0.4,P(W2)=0.2,P(W3)=0.8
Calculation:
P(W1)+P(W2)+P(W3)=0.4+0.2+0.8=1.4
Conclusion: The sum is greater than 1. Therefore, Option A is not valid.
Step 2: Check Option B
Probabilities: P(W1)=0,P(W2)=0,P(W3)=1
Calculation:
P(W1)+P(W2)+P(W3)=0+0+1=1
Conclusion: The sum equals 1, and all probabilities are non-negative. Therefore, Option B is valid.
Step 3: Check Option C
Probabilities: P(W1)=−12,P(W2)=34,P(W3)=12
Calculation:
P(W1)+P(W2)+P(W3)=−12+34+12
Converting to a common denominator (4):
=−24+34+24=34 (which is not equal to 1)
Conclusion: The sum is not equal to 1, and P(W1) is negative. Therefore, Option C is not valid.
Step 4: Check Option D
Probabilities: P(W1)=12,P(W2)=12,P(W3)=14
Calculation:
P(W1)+P(W2)+P(W3)=12+12+14
Converting to a common denominator (4):
=24+24+14=54 (which is greater than 1)
Conclusion: The sum is greater than 1. Therefore, Option D is not valid.
Final Conclusion
The only valid assignment of probability is Option B.
---
2. Each probability must be non-negative.
Probabilities: P(W1)=0.4,P(W2)=0.2,P(W3)=0.8
P(W1)+P(W2)+P(W3)=0.4+0.2+0.8=1.4
Probabilities: P(W1)=0,P(W2)=0,P(W3)=1
P(W1)+P(W2)+P(W3)=0+0+1=1
Probabilities: P(W1)=−12,P(W2)=34,P(W3)=12
P(W1)+P(W2)+P(W3)=−12+34+12
Converting to a common denominator (4):
=−24+34+24=34 (which is not equal to 1)
Probabilities: P(W1)=12,P(W2)=12,P(W3)=14
P(W1)+P(W2)+P(W3)=12+12+14
Converting to a common denominator (4):
=24+24+14=54 (which is greater than 1)
The only valid assignment of probability is Option B.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - TRY YOURSELF42videos
PROBABILITY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - ASSIGNMENT (SECTION - A Competition Level Questions)114videos
PROBABILITY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)11videos
PRINCIPLE OF MATHEMATICAL
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - J) Aakash Challengers Questions8videos
RELATIONS AND FUNCTIONS
Similar Questions
Which of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
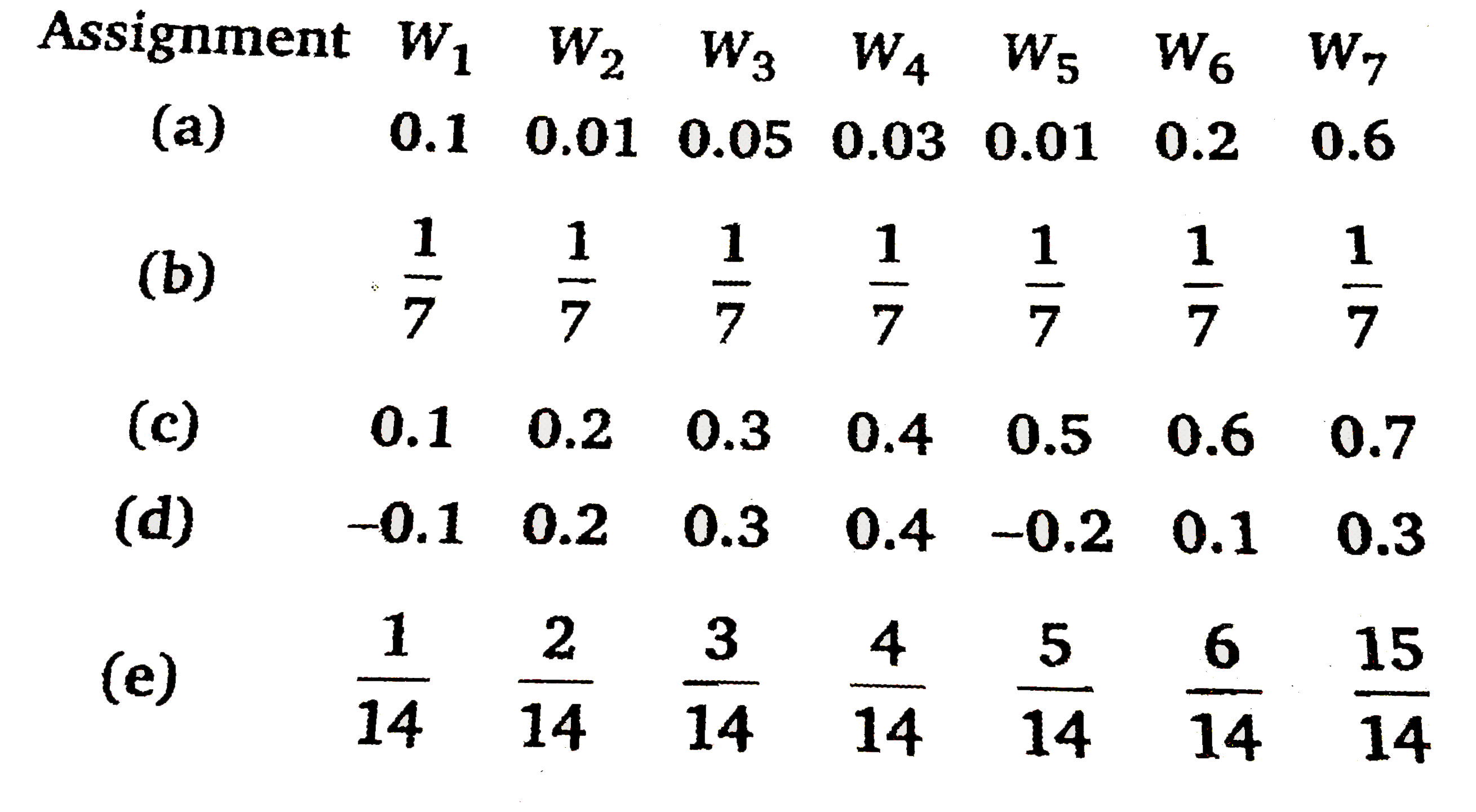 View Solution
View SolutionWhich of the following cannot be valid assignment of probability for elementary events or outcomes of samples space S={w1,w2,w3,w4,w5,w6,w7}: Elementary events w1 w2 w3 w4 w5 w6 w7 i. 0.1 0.01 0.05 0.03 0.01 0.2 0.6 ii. 17 17 17 17 17 17 17 iii. 0.7 0.6 0.5 0.4 0.3 0.2 0.1 iv. 114 214 314 414 514 614 1514
View Solution
Knowledge Check
- Question 1 - Select One
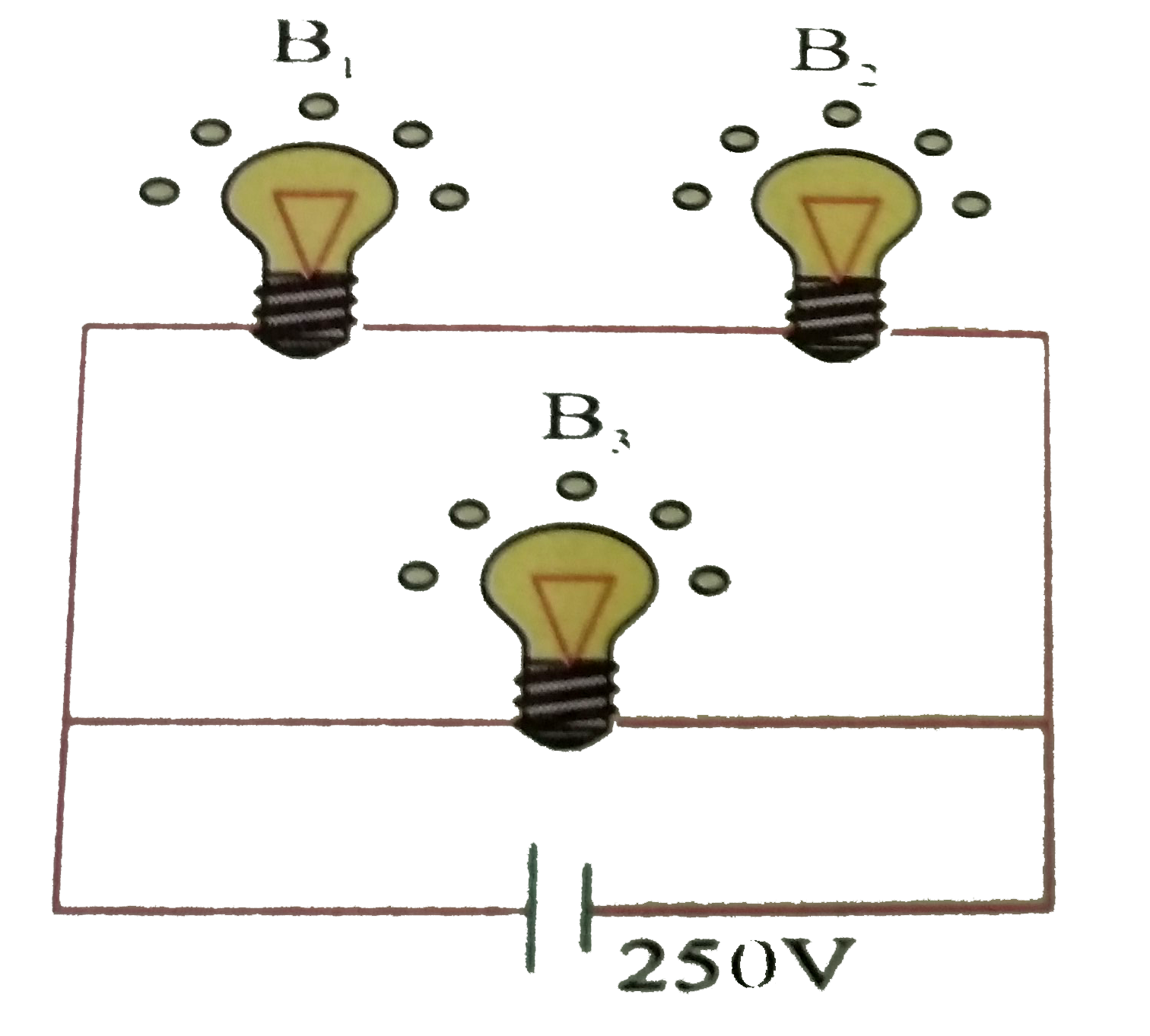
A 100 W bulb B1 and two 60 W bulbs B2 and B3, are connected to a 250V source, as shown in the figure now W1,W2 and W3 are the output powers of the bulbs B1,B2 and B3 respectively thenAW1>W2=W3BW1>W2>W3CW1<W2=W3DW1<W2<W3 - Question 2 - Select One

A 100 W bulb B1 and two 60 W bulbs B2 and B3, are connected to a 250V source, as shown in the figure now W1,W2 and W3 are the output powers of the bulbs B1,B2 and B3 respectively thenAW1>W2=W3BW1>W2>W3CW1<W2=W3DW1<W2<W3 - Question 3 - Select One
If the sample space of a random experiment is S={w1,w2,...,w6}, then which of the following arrangements of probability are valid?
 A(i) and (iii) onlyB(i) , (ii) and (iii) onlyC(i) and (ii) onlyD(i) , (ii) , (iii) and (iv)
A(i) and (iii) onlyB(i) , (ii) and (iii) onlyC(i) and (ii) onlyD(i) , (ii) , (iii) and (iv)
In the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
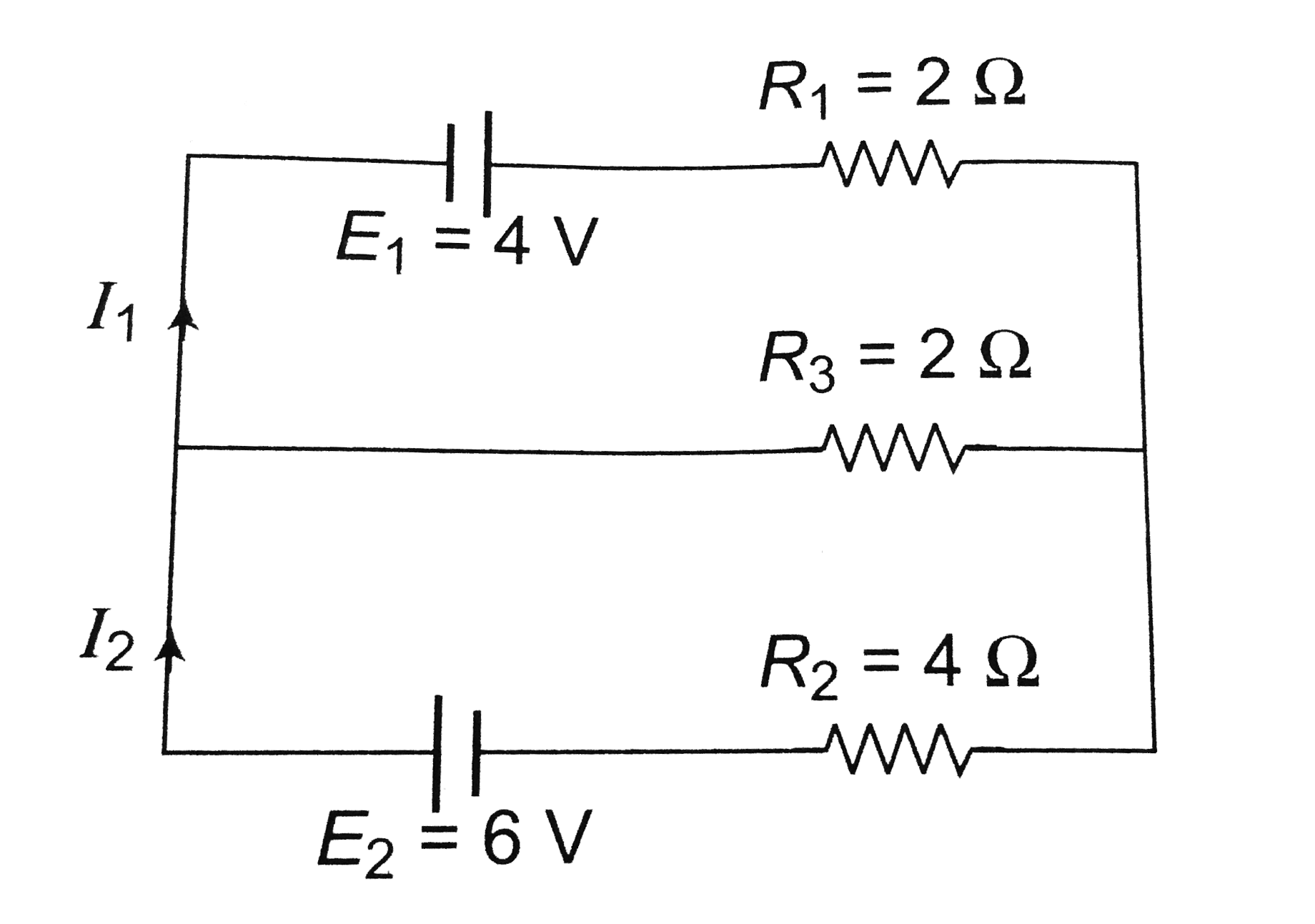 View Solution
View SolutionIf ω be an imaginary cube root of unity, show that 1+ωn+ω2n=0,for n=2,4
View SolutionProve the following
(1−ω+ω2)(1+ω−ω2)(1−ω−ω2)=8View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
ω28+ω29+1=0View SolutionTwo weights W1 and W2 in equilibrium and at rest, are suspended as shown in figure. Then the ratio W1W2 is :
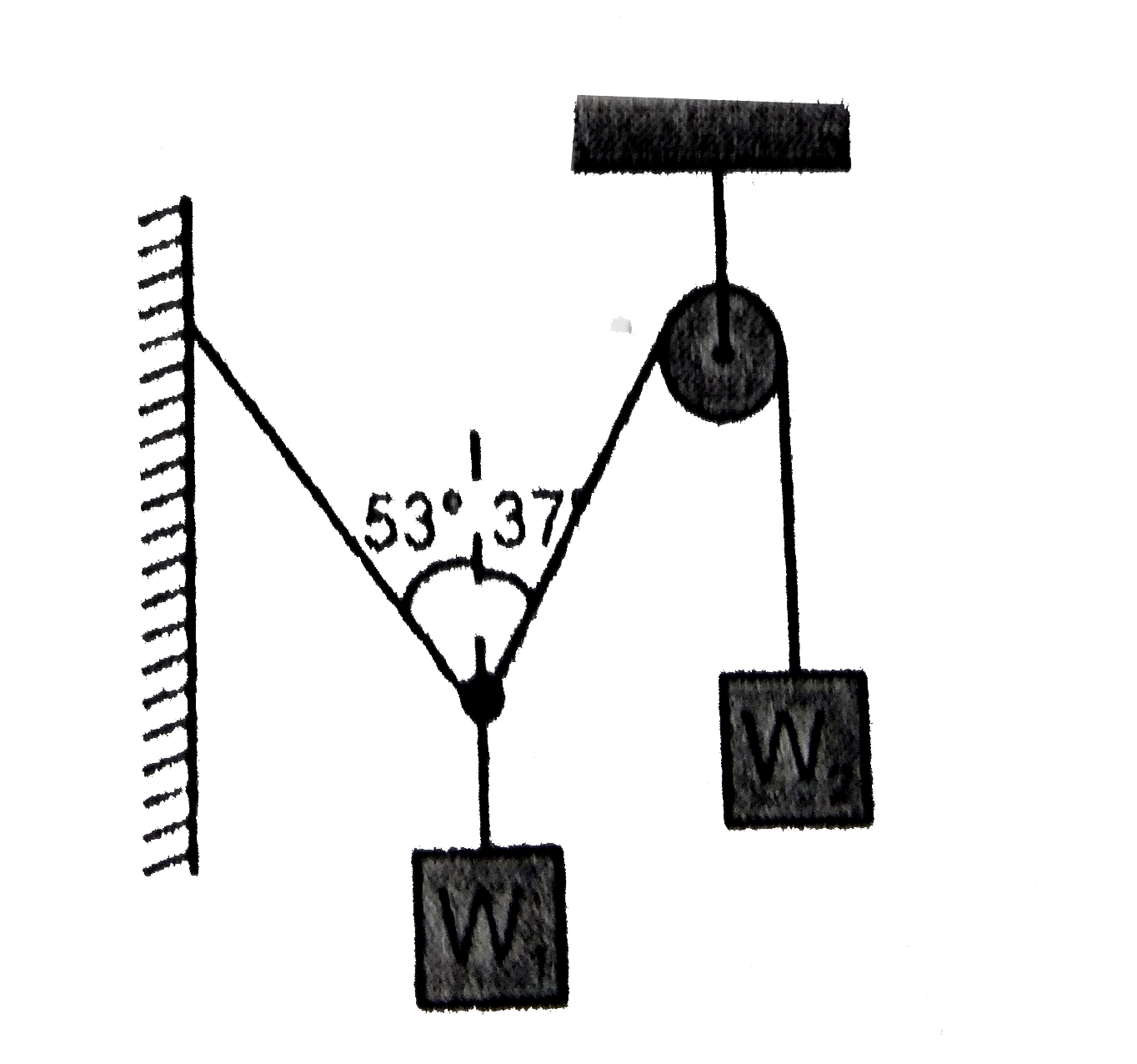 View Solution
View Solution

