A friendly hockey match among Aakashians played from 3pm to 5pm. Shekhar arrives to see the match (not before the match starts). Find the probability that the will miss the only goal of the match which takes place at the 15th minute of the match.
To solve the problem, we need to find the probability that Shekhar will miss the only goal of the hockey match, which occurs at the 15th minute. Here’s a step-by-step breakdown of the solution:
Step 1: Determine the Duration of the Match
The hockey match is played from 3 PM to 5 PM.
- Duration = 5 PM - 3 PM = 2 hours = 120 minutes.
Hint: Always convert the time duration into a single unit (minutes in this case) for easier calculations.
Step 2: Identify the Time of the Goal
The goal occurs at the 15th minute of the match, which is:
- 3 PM + 15 minutes = 3:15 PM.
Hint: Mark important events (like the goal) on your timeline to visualize the situation better.
Step 3: Determine the Time Shekhar Misses the Goal
Shekhar will miss the goal if he arrives after the goal has been scored. Therefore, he must arrive between:
- 3:15 PM and 5 PM.
Hint: Identify the intervals where the event (goal) has already occurred to determine when it can be missed.
Step 4: Calculate the Duration During Which Shekhar Can Miss the Goal
The time interval during which Shekhar can miss the goal is from 3:15 PM to 5 PM:
- Duration = 5 PM - 3:15 PM = 1 hour 45 minutes = 105 minutes.
Hint: Subtract the start time of missing the event from the end time to find the duration.
Step 5: Calculate the Total Possible Arrival Times
The total time frame for Shekhar to arrive at the match is the entire duration of the match:
- Total duration = 120 minutes.
Hint: Always consider the total possible outcomes when calculating probabilities.
Step 6: Calculate the Probability of Missing the Goal
The probability that Shekhar misses the goal is given by the ratio of the time he can miss the goal to the total time of the match:
Probability=Favorable outcomesTotal outcomes=105 minutes120 minutes.
Step 7: Simplify the Probability
Now, simplify the fraction:
105120=78 (by dividing both the numerator and denominator by 15).
Hint: Always simplify fractions to their lowest terms for clarity.
Final Answer
The probability that Shekhar will miss the only goal of the match is:
78.
The hockey match is played from 3 PM to 5 PM.
- Duration = 5 PM - 3 PM = 2 hours = 120 minutes.
The goal occurs at the 15th minute of the match, which is:
- 3 PM + 15 minutes = 3:15 PM.
Shekhar will miss the goal if he arrives after the goal has been scored. Therefore, he must arrive between:
- 3:15 PM and 5 PM.
The time interval during which Shekhar can miss the goal is from 3:15 PM to 5 PM:
- Duration = 5 PM - 3:15 PM = 1 hour 45 minutes = 105 minutes.
The total time frame for Shekhar to arrive at the match is the entire duration of the match:
- Total duration = 120 minutes.
The probability that Shekhar misses the goal is given by the ratio of the time he can miss the goal to the total time of the match:
Probability=Favorable outcomesTotal outcomes=105 minutes120 minutes.
Now, simplify the fraction:
105120=78 (by dividing both the numerator and denominator by 15).
The probability that Shekhar will miss the only goal of the match is:
78.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - TRY YOURSELF42videos
PROBABILITY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - ASSIGNMENT (SECTION - A Competition Level Questions)114videos
PROBABILITY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)11videos
PRINCIPLE OF MATHEMATICAL
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - J) Aakash Challengers Questions8videos
RELATIONS AND FUNCTIONS
Similar Questions
In a hockey match, both teams A and B scored same number of goals upto the end of the game, so to decide the winner, the referee asked both the captains to throw a die alternatively and decide that the team, whose captain gets a first six, will be declared the winner. If the captain of team A was asked to start, find their respective probabilities of winning the match and state whether the decision of the refree was fair or not.
View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
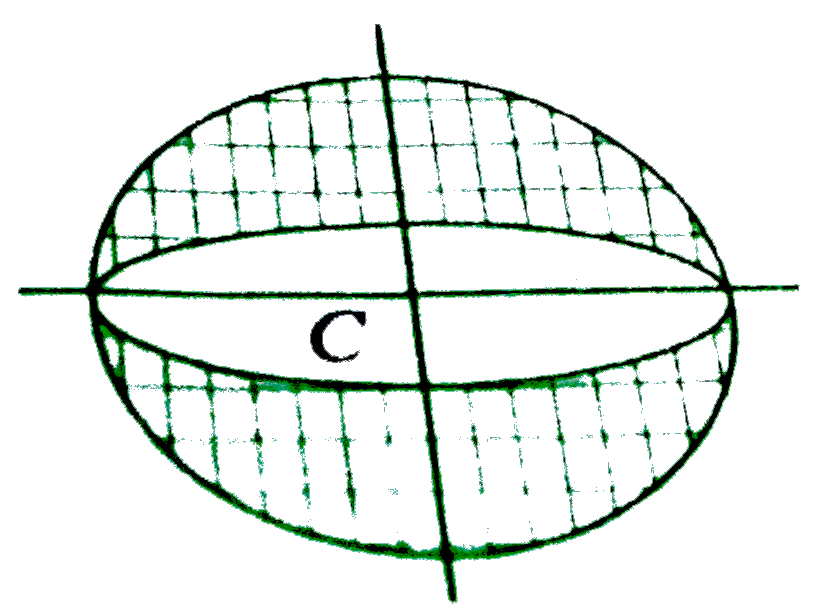
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00 (hh:mm:ss:100 th part of the second). Find the value of g. (correct upt ot two decimal places).View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet isView SolutionIndia plays 4 matches with Australia. The probability of india winning a match is 34 and loosing match is 14. Find the probability of india winning 3rd time in 4th match.
View SolutionA tennis match of best of 5 sets is played by two players A and B. The probability that first set is won by A is 1/2 and if he losed the first, then probability of his winning the next set is 1/4, otherwise it remains same. Find the probability that A wins the match.
View SolutionIn a T-20 tournament, there are five teams. Each teams plays one match against every other team.
Each team has 50% chance of winning any game it plays. No match ends in a tie.
Statement-1: The Probability that there is an undefeated team in the tournament is 516.
Statment-2: The probability that there is a winless team is the tournament is 316.View SolutionA and B play a game of tennis. The situation of the game is as follows: if one scores two consecutive points after a deuce, he wins; if loss of a point is followed by win of a point, it is deuce. The chance of a server to win a point is 2/3. The game is a deuce and A is serving. Probability that A will win the match is (serves are change after each game) 3/5 b. 2/5 c. 1/2 d. 4/5
View SolutionSuppose the probability for A to win a game against B is 0.4. If A has an option of playing either a “best of 3 games'' or a “best of 5 games match against B, which option should be chosen so that the probability of his winning the match is higher? (No game ends in a draw.)
View SolutionSuppose the probability for A to win a game against B is 0.4. If A has an option of playing either a “best of 3 games'' or a “best of 5 games match against B, which option should be chosen so that the probability of his winning the match is higher? (No game ends in a draw.)
View SolutionTwo players P1, and P2, are playing the final of a chase championship, which consists of a series of match Probability of P1, winning a match is 2/3 and that of P2 is 1/3. The winner will be the one who is ahead by 2 games as compared to the other player and wins at least 6 games. Now, if the player P2, wins the first four matches find the probability of P1, wining the championship.
View Solution

