A block of mass m on a smooth horizontal surface is. Connected to a second mass 2m by a light cord over a light frictionless pulley as shown. ( Neglect the mass of the cord and of the pulley). A force of magnitude F0 is applied to mass m as shown. Neglect any fiction . Find the value of force F0 for which the system will be in equilibrium
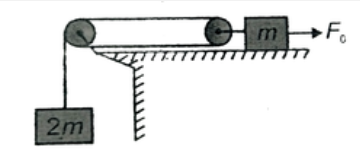
mg
2mg
3 mg
4mg
The correct Answer is:D
Step by step video & image solution for A block of mass m on a smooth horizontal surface is. Connected to a second mass 2m by a light cord over a light frictionless pulley as shown. ( Neglect the mass of the cord and of the pulley). A force of magnitude F_(0) is applied to mass m as shown. Neglect any fiction . Find the value of force F_(0) for which the system will be in equilibrium by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -C) objective type questions (More than one options are correct)
21 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question
1 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -A)
50 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A block of mass m1 on asmooth, horizontal surface is connected to a second mass m2 by a light string over a height, frictionless pulley. A force of magnitude F0 is applied to mass m1. Find the value of force F0 for which the system will be is equilibrium.

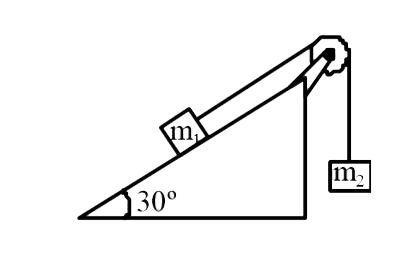
View SolutionA block of mass m1=2kg on a smooth inclined planeat angle 30∘ is connected to a second block of mass m2=3kg by a cord passing over a frictionless pulley as shown in figure. The acceleration of each block is - (Assume g=10m/sec2 )
View SolutionA block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and surface is 0.5. Tension in the cord is (take, g=9.8ms−2)

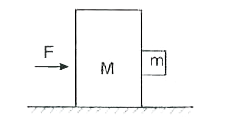
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
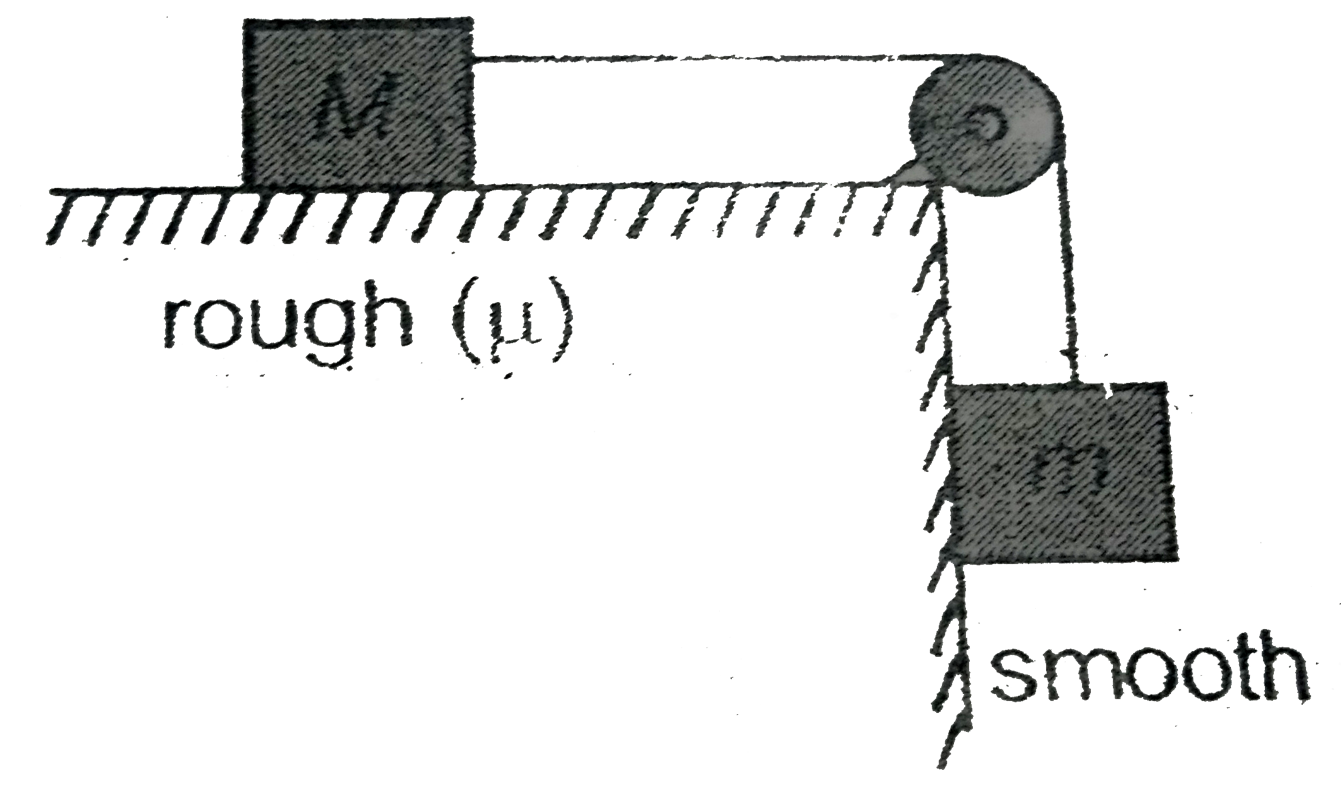
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View SolutionTwo particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
View SolutionA block of mass 20 kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in the figure. Find the acceleration of the pulley
_PHY_E05_192_Q05.png)
View SolutionA block of mass of 20kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in figure.Find the acceleration of the pulley
_PHY_E05_034_Q01.png) .jpg
.jpg
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
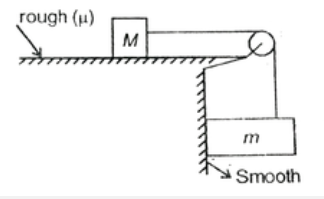
The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionIn the figure shown, all surfaces are smooth and the pulley is massless. A constant force of magnitude F=mg2 is acting on the block of mass M. The acceleration of the block M is :

View Solution
