Two particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
√2MmgM+m
MmgM+m
2MmgM+m
√3MmgM+m
The correct Answer is:A
To solve the problem of two particles of masses m and M (where M>m) connected by a cord over a massless, frictionless pulley, we need to find the tension T in the string and the acceleration a of the particles.
1. Identify Forces Acting on Each Mass:
- For mass m (the lighter mass), the forces acting on it are:
- Tension T acting upward.
- Weight mg acting downward.
- For mass M (the heavier mass), the forces acting on it are:
- Weight Mg acting downward.
- Tension T acting upward.
2. Write the Equations of Motion:
- For mass m:
T−mg=ma(Equation 1)
- For mass M:
Mg−T=Ma(Equation 2)
3. Add the Two Equations:
- Adding Equation 1 and Equation 2:
(T−mg)+(Mg−T)=ma+Ma
- This simplifies to:
Mg−mg=(m+M)a
4. Solve for Acceleration a:
- Rearranging the equation gives:
(M−m)g=(m+M)a
- Thus, the acceleration a is:
a=(M−m)gm+M
5. Substitute a Back to Find Tension T:
- Substitute a into Equation 1:
T−mg=m((M−m)gm+M)
- Rearranging gives:
T=mg+m((M−m)gm+M)
6. Simplify the Expression for Tension T:
- Factor out g:
T=g(m+m(M−m)m+M)
- Combine the terms:
T=g(m(m+M)+m(M−m)m+M)
- This simplifies to:
T=g(mM+mgm+M)
7. Final Expression for Tension T:
- The final expression for tension T is:
T=2mMgm+M
Summary of Results:
- The acceleration a of the particles is:
a=(M−m)gm+M
- The tension T in the string is:
T=2mMgm+M
- For mass m (the lighter mass), the forces acting on it are:
- Tension T acting upward.
- Weight mg acting downward.
- For mass M (the heavier mass), the forces acting on it are:
- Weight Mg acting downward.
- Tension T acting upward.
- For mass m:
T−mg=ma(Equation 1)
- For mass M:
Mg−T=Ma(Equation 2)
- Adding Equation 1 and Equation 2:
(T−mg)+(Mg−T)=ma+Ma
- This simplifies to:
Mg−mg=(m+M)a
- Rearranging the equation gives:
(M−m)g=(m+M)a
- Thus, the acceleration a is:
a=(M−m)gm+M
- Substitute a into Equation 1:
T−mg=m((M−m)gm+M)
- Rearranging gives:
T=mg+m((M−m)gm+M)
- Factor out g:
T=g(m+m(M−m)m+M)
- Combine the terms:
T=g(m(m+M)+m(M−m)m+M)
- This simplifies to:
T=g(mM+mgm+M)
- The final expression for tension T is:
T=2mMgm+M
- The acceleration a of the particles is:
a=(M−m)gm+M
- The tension T in the string is:
T=2mMgm+M
Similar Questions
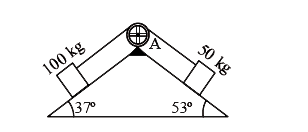
Two blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
View SolutionConsider two objects of different masses connected by a cable passing over a massless and frictionless Pulley. Derive expressions for the tension in the cable and acceleration of the objects.
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration

View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
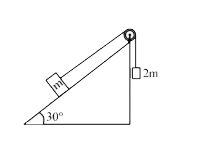
View SolutionTwo blocks of masses m and 2m are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass m is placed on a smooth inclined plane of inclination 30° and 2m hangs vertically. If the system is released, the blocks move with an acceleration equal to :
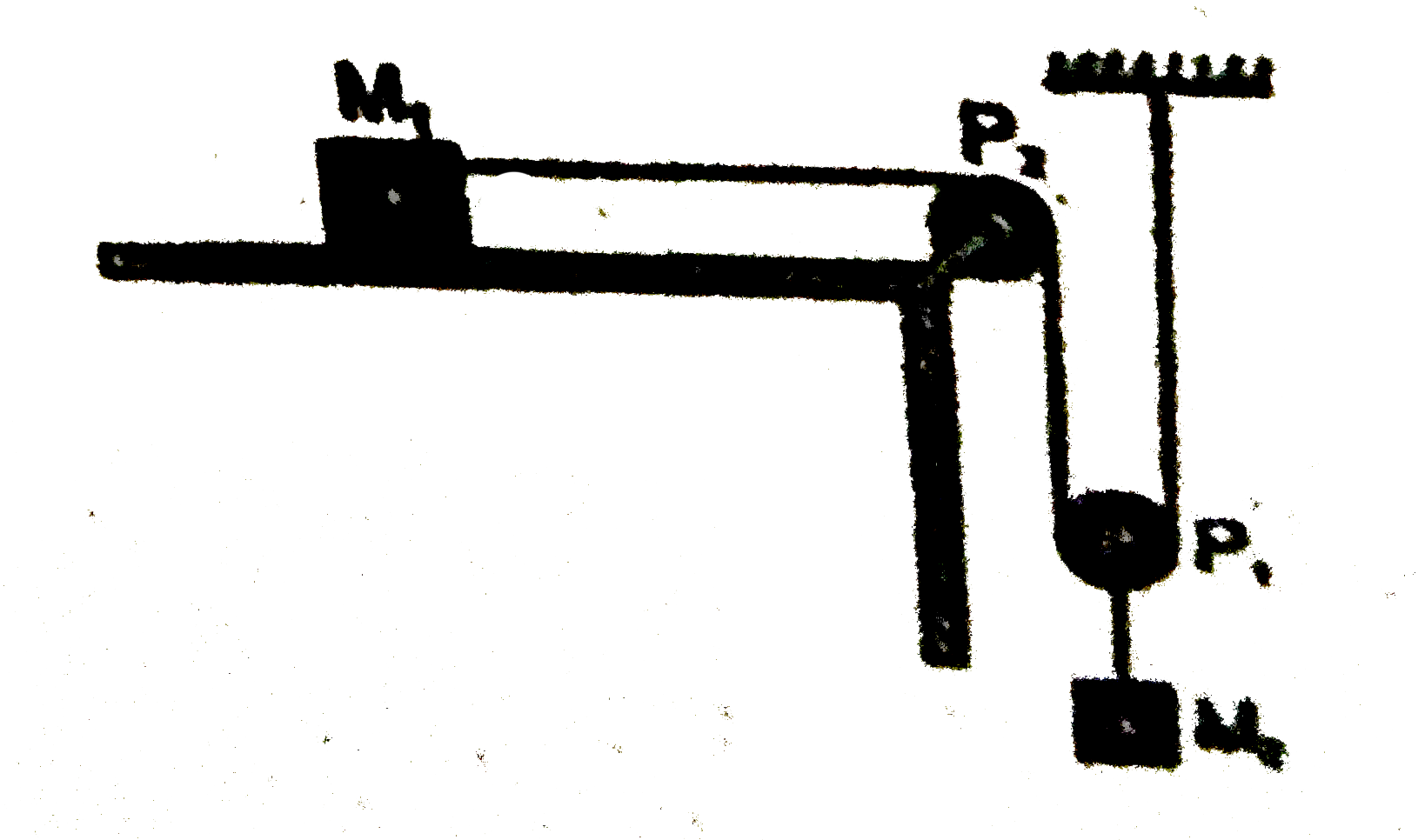
View SolutionBlocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
View SolutionA block of mass M1=3kg on a smooth fixed inclined plane of angle 30∘ is connected by a cord over a small frictionless pulley to a second block mass 2kg hanging vertically. The tension in the cord and the acceleration of each block are ………............. and ...................... respectively.

View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View Solution