In the arrangement shown in figure in which four blocks are suspended by cords . The top card loops over a frictionless pulley and pulls with a force of magnitude 98 N on the wall to which is attached . If the tensions in the shorter cords are T1=58.8N,T2=49.0andT3=9.8N,
The correct Answer is:4
To solve the problem, we need to analyze the forces acting on each block and use the given tensions to find the masses of the blocks A, B, C, and D.
1. Understanding the Forces:
- The system consists of four blocks (A, B, C, D) suspended by cords over a frictionless pulley.
- The top cord pulls with a force of 98 N.
- The tensions in the cords are given as:
- T1=58.8N
- T2=49.0N
- T3=9.8N
2. Finding the Mass of Block D:
- The tension T3 is the force acting on block D (the lowest block).
- Using the formula for tension, T=mg, where g=9.8m/s2:
T3=mD⋅g⟹9.8=mD⋅9.8
- Solving for mD:
mD=1.0kg
3. Finding the Mass of Block C:
- The tension T2 supports both block C and block D.
- The equation for block C becomes:
T2=mC⋅g+T3
- Substituting the known values:
49.0=mC⋅9.8+9.8
- Rearranging gives:
49.0−9.8=mC⋅9.8⟹39.2=mC⋅9.8
- Solving for mC:
mC=39.29.8=4.0kg
4. Finding the Mass of Block B:
- The tension T1 supports blocks A and B, as well as the weight of block C.
- The equation for block B becomes:
T1=mB⋅g+T2
- Substituting the known values:
58.8=mB⋅9.8+49.0
- Rearranging gives:
58.8−49.0=mB⋅9.8⟹9.8=mB⋅9.8
- Solving for mB:
mB=1.0kg
5. Finding the Mass of Block A:
- The total weight supported by the top cord (which is equal to the pulling force of 98 N) is the sum of the weights of blocks A, B, and C:
- The equation becomes:
98=mA⋅g+T1
- Substituting the known values:
98=mA⋅9.8+58.8
- Rearranging gives:
98−58.8=mA⋅9.8⟹39.2=mA⋅9.8
- Solving for mA:
mA=39.29.8=4.0kg
Summary of Masses:
- mA=4.0kg
- mB=1.0kg
- mC=4.0kg
- mD=1.0kg
- The system consists of four blocks (A, B, C, D) suspended by cords over a frictionless pulley.
- The top cord pulls with a force of 98 N.
- The tensions in the cords are given as:
- T1=58.8N
- T2=49.0N
- T3=9.8N
- The tension T3 is the force acting on block D (the lowest block).
- Using the formula for tension, T=mg, where g=9.8m/s2:
T3=mD⋅g⟹9.8=mD⋅9.8
- Solving for mD:
mD=1.0kg
- The tension T2 supports both block C and block D.
- The equation for block C becomes:
T2=mC⋅g+T3
- Substituting the known values:
49.0=mC⋅9.8+9.8
- Rearranging gives:
49.0−9.8=mC⋅9.8⟹39.2=mC⋅9.8
- Solving for mC:
mC=39.29.8=4.0kg
- The tension T1 supports blocks A and B, as well as the weight of block C.
- The equation for block B becomes:
T1=mB⋅g+T2
- Substituting the known values:
58.8=mB⋅9.8+49.0
- Rearranging gives:
58.8−49.0=mB⋅9.8⟹9.8=mB⋅9.8
- Solving for mB:
mB=1.0kg
- The total weight supported by the top cord (which is equal to the pulling force of 98 N) is the sum of the weights of blocks A, B, and C:
- The equation becomes:
98=mA⋅g+T1
- Substituting the known values:
98=mA⋅9.8+58.8
- Rearranging gives:
98−58.8=mA⋅9.8⟹39.2=mA⋅9.8
- Solving for mA:
mA=39.29.8=4.0kg
- mA=4.0kg
- mB=1.0kg
- mC=4.0kg
- mD=1.0kg
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -H ) Multiple True - False Type Questions (Identify the correct combination of true (T) and false (F) of the given three statements.)8videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -I ) Subjective Type Questions9videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -F ) Matrix - Match Type Questions4videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)26videos
MAGNETISM AND MATTER
Similar Questions
For the arrangement shown in figure, angle θ for which tension T1 in the left string will be minimum is (Pulley and strings are ideal)
 View Solution
View SolutionThree masses are connected as shown in figure on a horizontal frictionless surface and pulled by a force of 60 N. The tensions T1andT2 are in the ratio
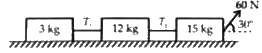 View Solution
View SolutionIn the figure shown, m1 = 10kg, m2 = 6kg, m3 = 4kg. If T3 = 40 N, T2 = ?
 View Solution
View SolutionThree ants 1, 2 and 3 are pulling a grain with forces of magnitudes 2N√3N and √2N and as shown in the figure. Find the resultant force acting on the grain.
 View Solution
View SolutionA block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and surface is 0.5. Tension in the cord is (take, g=9.8ms−2)
 View Solution
View SolutionTwo blocks of mass 8 kg and 5 kg are connected by a heavy rope of mass 3 kg. An upward force of 180 N is applied as shown in the figure. The tension in the string at point P will be:
 View Solution
View SolutionFour blocks of the same mass m connected by cords are pulled by a force F on a smooth horizontal surface as shown in Determine the tensions T1,T2 and T3 in the cords.
View SolutionA block A of mass 8 kg is placed on a frictionless horizontal table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 2 kg at the other end. Find the acceleration of the system. Also find the tension in the thread. If the thread is cut into two and tied to the ends of a spring of forceconstant 1600N/m, find the amount of stretching of the spring. Neglect the mass of thread and of spring (g=9.8m/s2)
View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B
 View Solution
View SolutionThree blocks of masses m1,m2andm3 are connected by mass less string as shown kept on a frictionless table.

They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, the tension T2 will beView Solution

