Four blocks of the same mass m connected by cords are pulled by a force F on a smooth horizontal surface as shown in Determine the tensions T1,T2 and T3 in the cords.
T1=14F,T2=32F,T3=14F
T1=14F,T2=12F,T3=12F
T1=34F,T2=12F,T3=14F
T1=34F,T2=12F,T3=12F
The correct Answer is:C
To solve the problem of determining the tensions T1,T2, and T3 in the cords connecting four blocks of mass m being pulled by a force F on a smooth horizontal surface, we will follow these steps:
Step 1: Determine the acceleration of the system
The total mass of the system is 4m (since there are four blocks, each of mass m). According to Newton's second law, the net force acting on the system is equal to the total mass times the acceleration:
F=(4m)⋅a
From this, we can solve for the acceleration a:
a=F4m
Step 2: Analyze the forces on the last block
For the last block (Block 4), the only force acting on it is the tension T3 in the cord connected to it. According to Newton's second law:
T3=m⋅a
Substituting the value of a:
T3=m⋅F4m=F4
Step 3: Analyze the forces on the third block
For the third block (Block 3), the forces acting on it are the tension T2 pulling it forward and the tension T3 pulling it backward. Thus, we can write:
T2−T3=m⋅a
Substituting the value of a and T3:
T2−F4=m⋅F4m
This simplifies to:
T2−F4=F4
Solving for T2:
T2=F4+F4=F2
Step 4: Analyze the forces on the second block
For the second block (Block 2), the forces acting on it are the tension T1 pulling it forward and the tension T2 pulling it backward. Thus, we can write:
T1−T2=m⋅a
Substituting the value of a and T2:
T1−F2=m⋅F4m
This simplifies to:
T1−F2=F4
Solving for T1:
T1=F2+F4=2F4+F4=3F4
Final Results
The tensions in the cords are:
- T1=3F4
- T2=F2
- T3=F4
The total mass of the system is 4m (since there are four blocks, each of mass m). According to Newton's second law, the net force acting on the system is equal to the total mass times the acceleration:
For the last block (Block 4), the only force acting on it is the tension T3 in the cord connected to it. According to Newton's second law:
For the third block (Block 3), the forces acting on it are the tension T2 pulling it forward and the tension T3 pulling it backward. Thus, we can write:
For the second block (Block 2), the forces acting on it are the tension T1 pulling it forward and the tension T2 pulling it backward. Thus, we can write:
The tensions in the cords are:
- T1=3F4
- T2=F2
- T3=F4
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved Papers 2017(JIPMER)
Explore 28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(NEET)
Explore 22 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Integer type questions
Explore 14 Videos
- SOUND WAVESBook:DC PANDEY ENGLISHChapter:SOUND WAVESExercise:Exercise 19.7
Explore 4 Videos
Similar Questions
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two blocks of masses 'M' and 'm' are placed on one another on a smooth horizontal surface as shown in the figure. The force 'F' is acting on the mass 'M' horizontally during time interval 't'. Assumings no relative sliding between the blocks, The work done by friction on the blocks is
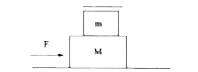
View SolutionThree masses are connected as shown in figure on a horizontal frictionless surface and pulled by a force of 60 N. The tensions T1andT2 are in the ratio
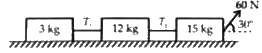
View SolutionTwo blocks A and B of the same mass are joined by a light string and placed on a horizontal surface. An external horizontal force P acts on A. The tension in the string is T. The forces of static friction acting on A and B are F1 and F2 respectively. The limiting value of F1 and F2 is F0. As P is gradually increased.
View SolutionTwo blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :

View SolutionTwo blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View SolutionThree blocks connected together by strings are pulled along a horizontal surface by applying force F. If T3=36N, What is tension T2?
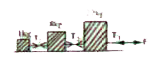
View Solution