Which of the following methods will enable the volume of an ideal gas to be made four times
Double the temperature and reduce the pressure to half
double the temperature and also double the pressure
reduce the temperature to half and double the pressure
reduce the temperature to half and reduce the pressure to half
The correct Answer is:A
To solve the problem of how to make the volume of an ideal gas four times its original volume, we can use the ideal gas law, which states:
PV=nRT
Where:
- P = pressure
- V = volume
- n = number of moles of gas (constant for this problem)
- R = ideal gas constant (constant for this problem)
- T = temperature in Kelvin
1. Understand the Relationship:
From the ideal gas law, we can derive that the volume V is directly proportional to the temperature T and inversely proportional to the pressure P:
V∝TP
2. Set Up the Equation:
To find the conditions under which the volume becomes four times its original value, we can express this mathematically:
V2=4V1
This can be rewritten using the proportionality:
V2V1=T2T1⋅P1P2
3. Substituting Values:
We need to manipulate the equation to achieve V2V1=4. This means:
4=T2T1⋅P1P2
4. Choose a Method:
Let's consider the first option: Double the temperature and reduce the pressure to half.
- If we double the temperature:
T2=2T1
- If we reduce the pressure to half:
P2=12P1
5. Calculate the New Volume:
Substitute these values into the equation:
V2V1=2T1T1⋅P112P1=2⋅2=4
Thus, V2=4V1.
6. Evaluate Other Options:
- Option 2: Double the temperature and double the pressure. This gives:
V2V1=2T1T1⋅P12P1=2⋅12=1(Incorrect)
- Option 3: Reduce the temperature to half and double the pressure. This gives:
V2V1=12T1T1⋅P12P1=12⋅12=14(Incorrect)
- Option 4: Reduce the temperature to half and reduce the pressure to half. This gives:
V2V1=12T1T1⋅P112P1=12⋅2=1(Incorrect)
Conclusion:
The only correct option that allows the volume of the gas to become four times its original volume is to double the temperature and reduce the pressure to half.
- P = pressure
- V = volume
- n = number of moles of gas (constant for this problem)
- R = ideal gas constant (constant for this problem)
- T = temperature in Kelvin
From the ideal gas law, we can derive that the volume V is directly proportional to the temperature T and inversely proportional to the pressure P:
V∝TP
To find the conditions under which the volume becomes four times its original value, we can express this mathematically:
V2=4V1
This can be rewritten using the proportionality:
V2V1=T2T1⋅P1P2
We need to manipulate the equation to achieve V2V1=4. This means:
4=T2T1⋅P1P2
Let's consider the first option: Double the temperature and reduce the pressure to half.
- If we double the temperature:
T2=2T1
- If we reduce the pressure to half:
P2=12P1
Substitute these values into the equation:
V2V1=2T1T1⋅P112P1=2⋅2=4
Thus, V2=4V1.
- Option 2: Double the temperature and double the pressure. This gives:
V2V1=2T1T1⋅P12P1=2⋅12=1(Incorrect)
- Option 3: Reduce the temperature to half and double the pressure. This gives:
V2V1=12T1T1⋅P12P1=12⋅12=14(Incorrect)
- Option 4: Reduce the temperature to half and reduce the pressure to half. This gives:
V2V1=12T1T1⋅P112P1=12⋅2=1(Incorrect)
The only correct option that allows the volume of the gas to become four times its original volume is to double the temperature and reduce the pressure to half.
Topper's Solved these Questions
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assignment (Section-B) Objective type questions (One option is correct)
10 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assignment (Section-C) Objective type questions (More than one option are correct)
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Try Yourself
43 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
Similar Questions
Knowledge Check
Which of the following graphs represent the behaviour of an ideal gas ?
A1.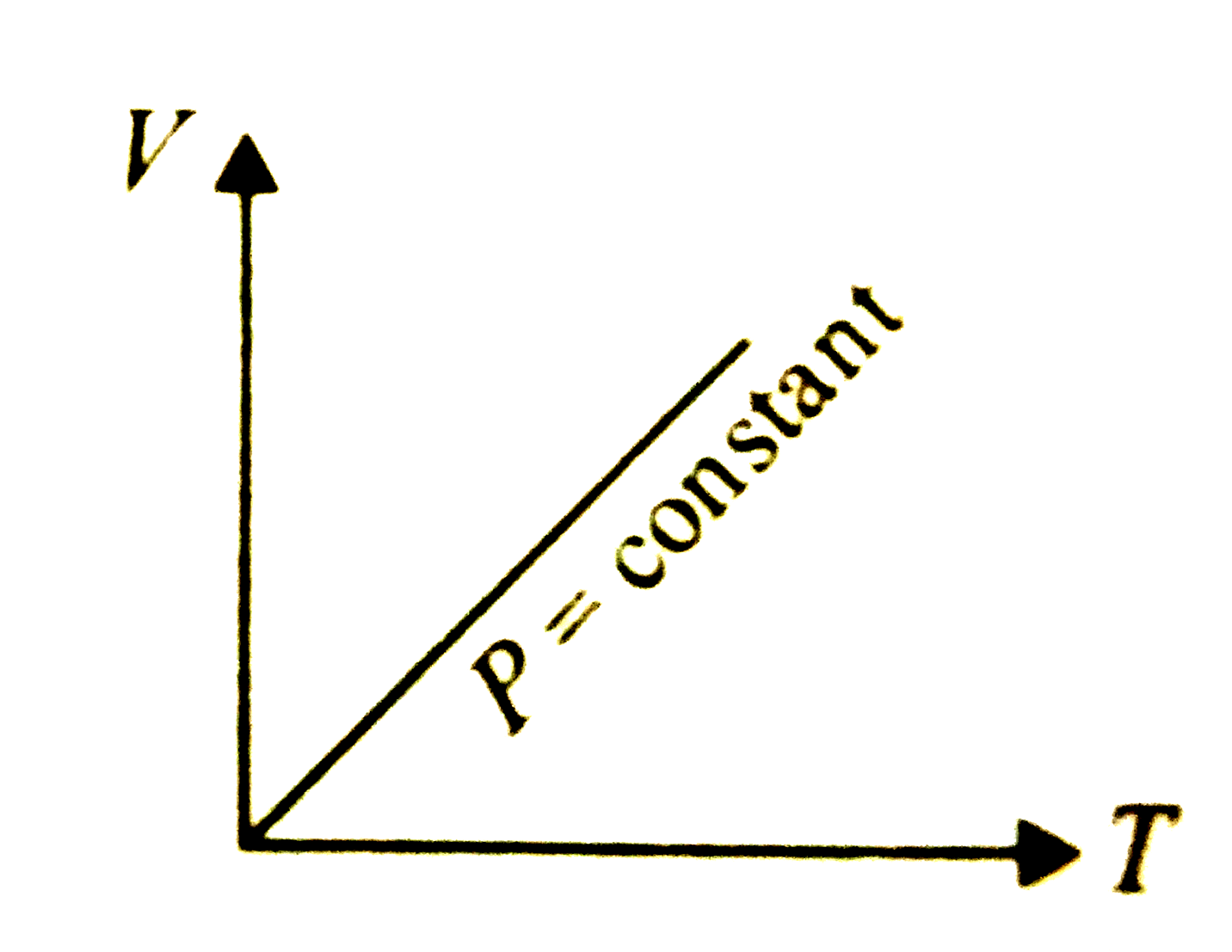 B2.
B2.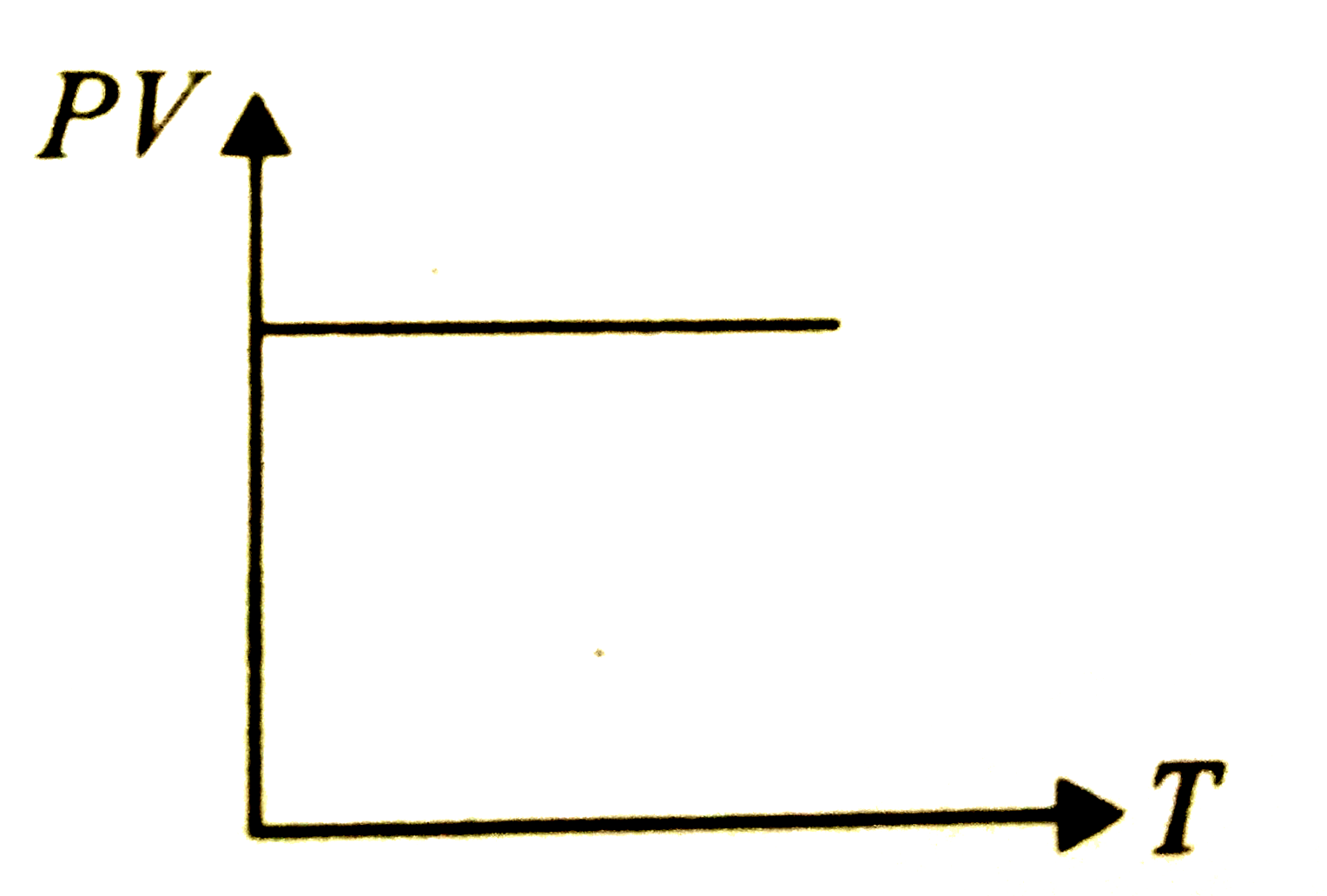 C3.
C3.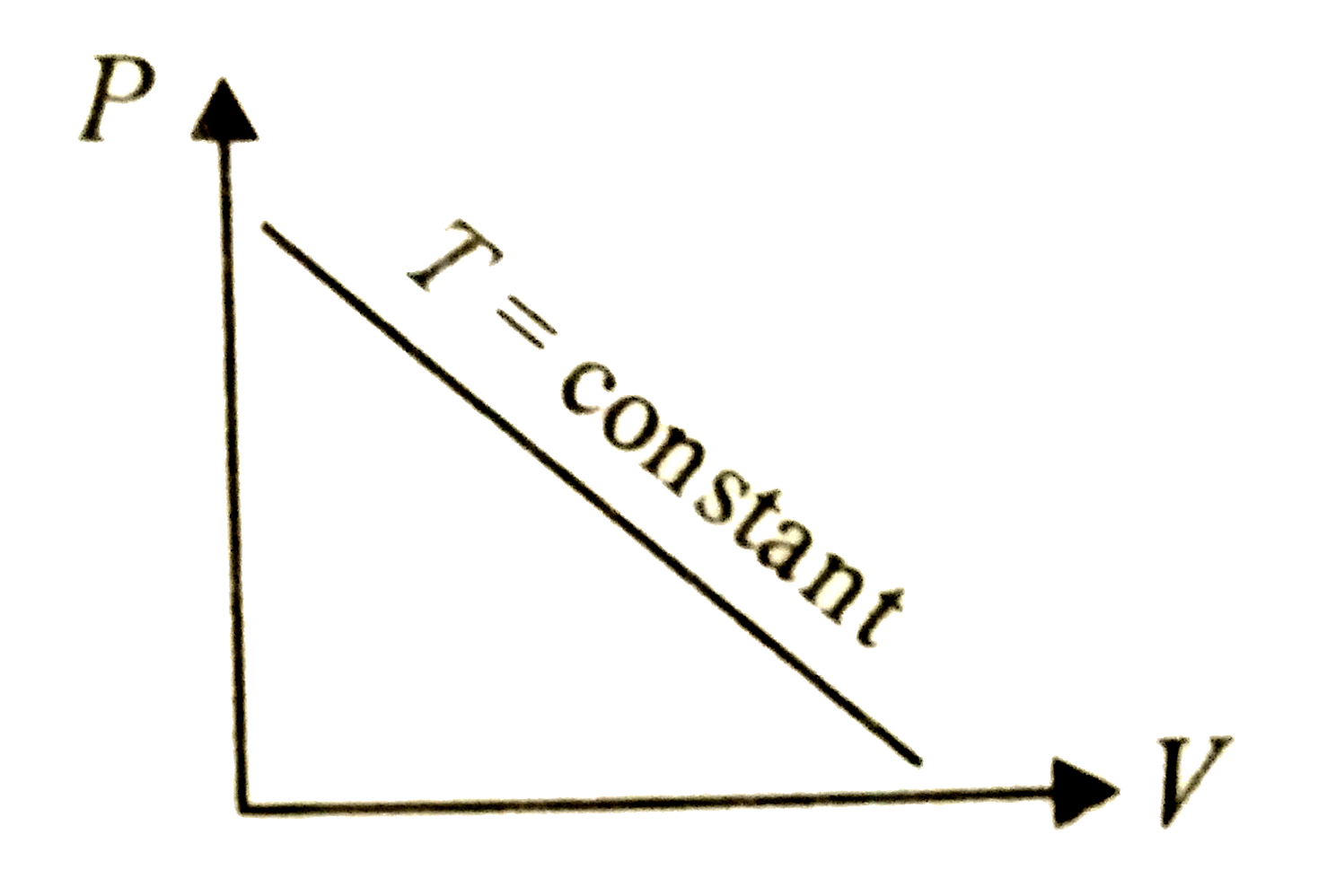 D4.
D4.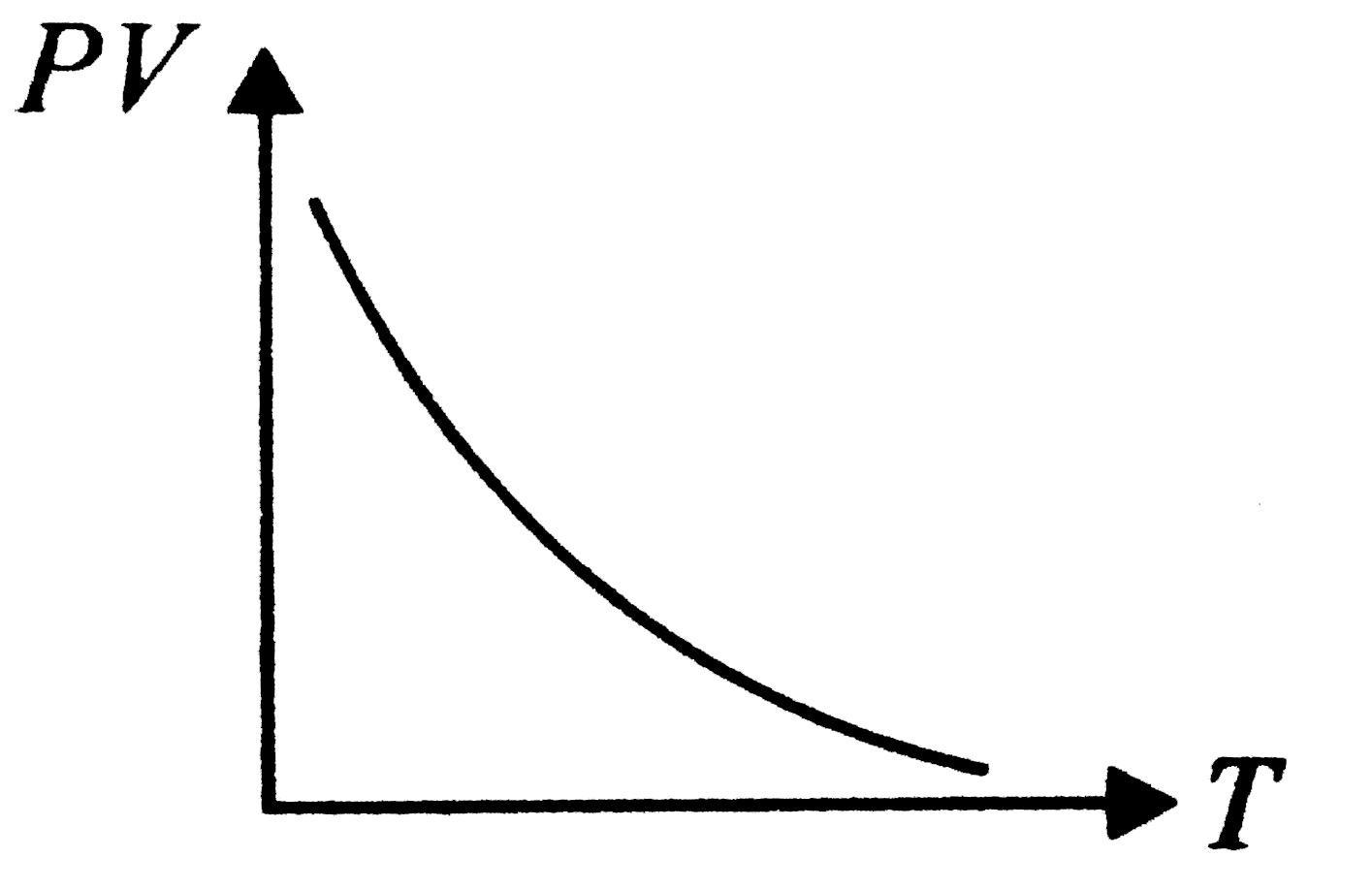
Which of the following expressions is true for an ideal gas ?
View SolutionWhich of the following relation is correct for an ideal gas ?
View SolutionWhich of the following graphs is consistent with ideal gas behaviour?
View SolutionBy which methods can the internal energy of an ideal gas be changed ?
View SolutionWhich of the following graph is incorrect for an ideal gas?
View SolutionWhich of the following does not represent ideal gas equation?
View SolutionWhich of the following curve is correct for an ideal gas ?
View Solution
