Calculate the magnitude and direction of the electric field at a point P which is 30 cm to the right of a point charge
To solve the problem of calculating the magnitude and direction of the electric field at point P, which is 30 cm to the right of a point charge Q=−3.0×10−6C, we will follow these steps:
Step 1: Convert the distance to meters
Given that the distance from the charge to point P is 30 cm, we need to convert this to meters.
R=30cm=0.30m
Step 2: Use the formula for electric field
The electric field E due to a point charge is given by the formula:
E=K⋅|Q|R2
where:
- K is Coulomb's constant, approximately 9×109N m2/C2
- Q is the charge
- R is the distance from the charge to the point where the electric field is being calculated
Step 3: Substitute the values into the formula
Substituting the values into the formula:
E=9×109⋅|−3.0×10−6|(0.30)2
Step 4: Calculate R2
Calculating R2:
R2=(0.30)2=0.09m2
Step 5: Substitute R2 into the electric field equation
Now substituting R2 back into the equation:
E=9×109⋅3.0×10−60.09
Step 6: Perform the multiplication and division
Calculating the numerator:
9×109⋅3.0×10−6=27×103=27000
Now divide by 0.09:
E=270000.09=300000N/C=3.0×105N/C
Step 7: Determine the direction of the electric field
Since the charge Q is negative, the electric field lines point towards the charge. Therefore, the direction of the electric field at point P (which is to the right of the charge) will be towards the left, towards the charge Q.
Final Answer
The magnitude of the electric field at point P is 3.0×105N/C and the direction is towards the left (towards the charge Q).
---
Given that the distance from the charge to point P is 30 cm, we need to convert this to meters.
The electric field E due to a point charge is given by the formula:
- K is Coulomb's constant, approximately 9×109N m2/C2
- Q is the charge
- R is the distance from the charge to the point where the electric field is being calculated
Substituting the values into the formula:
Calculating R2:
Now substituting R2 back into the equation:
Calculating the numerator:
Since the charge Q is negative, the electric field lines point towards the charge. Therefore, the direction of the electric field at point P (which is to the right of the charge) will be towards the left, towards the charge Q.
The magnitude of the electric field at point P is 3.0×105N/C and the direction is towards the left (towards the charge Q).
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - TRY YOURSELF33videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - ASSIGNMENT(SECTION-A) Objective Type Question45videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)10videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)15videos
ELECTROMAGNETIC INDUCTION
Similar Questions
The magnitude and direction of the electric field at point P can be best represented by
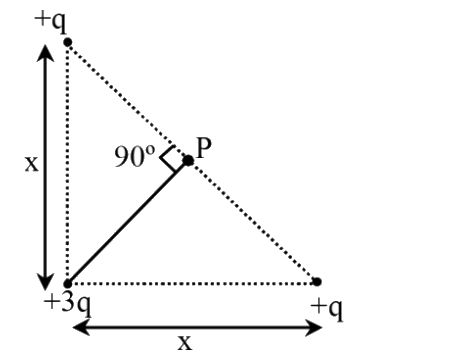 View Solution
View SolutionEvaluate magnitude and direction of magnetic field at a point P in the following cases
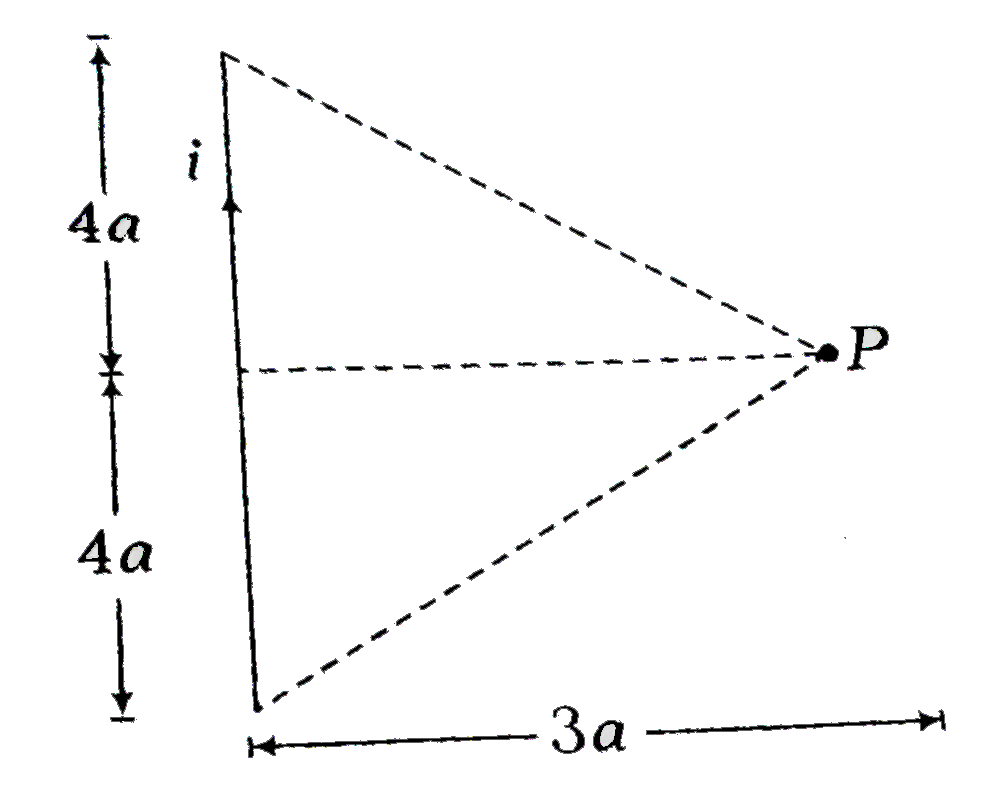
 View Solution
View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
View SolutionCalculate the magnitude of the electric field which can just balance a deuteron of mass 3.2×10−27kg
View SolutionCalculate the magnitude of the electric field which can just balance a deuteron of mass 3.2×10−27kg
View SolutionFour long, parallel conductors carry equal currents of 5.0. The direction of the currents is into the pge at points. A and B and out of the page at C and D. Calculate the magnitude and directionof the mgnetic field at point P, located at the centre of the square.
 View Solution
View SolutionAn electron is moving along +x direction with a velocity of 6×106ms−1 . It enters a region of uniform electric field of 300 V/cm pointing along + y direction. The magnitude and direction of the magnetic field set up in this region such that the electron keeps moving along the x direction will be :
View SolutionA particle having a charge+3×10−9C is placed in a uniform electric field directed toward left. It is released from rest and moves a distance of 5 cm after which its kinetic energy is found to be 4.5×10−5J.
(a) Calcnalate the work done by the electrical force on the particle
(b) Calculate the magnitude of the electric field.
(c) Calculate the potential of starting point with respect to the end point of particle's motion.View SolutionPositive point charge q=+8.00μCandq'=+3.00μC are moving relative to an observer in Fig. The distance d is 0.120m. When the two charges are at the locations shown in the figure, what are the magnitude and direction of the net magnetic field they produce at point P? (Takev=4.50×106ms−1andv'=9.00×106ms1)
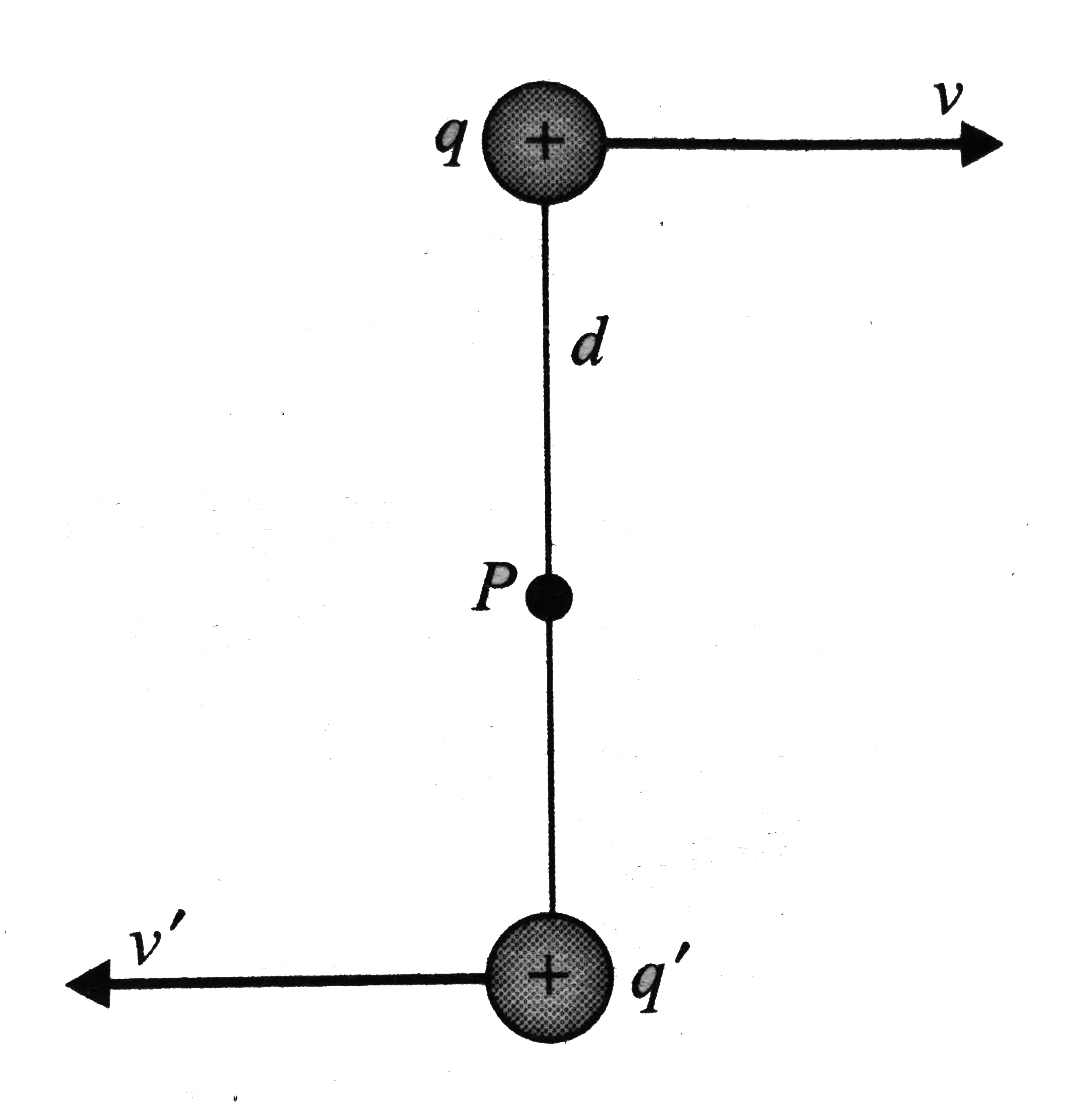 View Solution
View SolutionTwo equal and opposite charges of magnitude 0.2μC are 15 cm apart, the magnitude and direction of the resultant electric intensity at a point midway between the charges is
View Solution

