Find the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
To find the magnitude of the electric field at a point 4 cm away from a line charge with a linear charge density of λ=2×10−6C/m, we can follow these steps:
Step 1: Identify the formula for the electric field due to a line charge
The electric field E at a distance R from an infinitely long line charge with linear charge density λ is given by the formula:
E=2kλR
where k is the electrostatic constant, approximately 9×109N m2/C2.
Step 2: Convert the distance from cm to meters
The distance given is 4cm. We need to convert this into meters:
R=4cm=4×10−2m
Step 3: Substitute the values into the formula
Now, we can substitute the values of k, λ, and R into the formula:
E=2×(9×109)×(2×10−6)4×10−2
Step 4: Simplify the expression
Calculating the numerator:
2×(9×109)×(2×10−6)=36×103=3.6×104
Now, substituting this back into the equation:
E=3.6×1044×10−2
Step 5: Perform the division
Calculating the division:
E=3.6×1044×10−2=3.6×104×14×10−2=3.6×104×25=9×105N/C
Final Answer
Thus, the magnitude of the electric field at a point 4 cm away from the line charge is:
E=9×105N/C
---
The electric field E at a distance R from an infinitely long line charge with linear charge density λ is given by the formula:
E=2kλR
where k is the electrostatic constant, approximately 9×109N m2/C2.
The distance given is 4cm. We need to convert this into meters:
R=4cm=4×10−2m
Now, we can substitute the values of k, λ, and R into the formula:
E=2×(9×109)×(2×10−6)4×10−2
Calculating the numerator:
2×(9×109)×(2×10−6)=36×103=3.6×104
Now, substituting this back into the equation:
E=3.6×1044×10−2
Calculating the division:
E=3.6×1044×10−2=3.6×104×14×10−2=3.6×104×25=9×105N/C
Thus, the magnitude of the electric field at a point 4 cm away from the line charge is:
E=9×105N/C
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 28videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
Similar Questions
A 10 cm long rod carries a charge of +150μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
View SolutionA Charge of 4×10−8C is distributed uniformaly on the surface of a sphere of radius 1 cm. It is covered by a concentric, hollow conducting sphere of radius 5 cm. (a) Find the electric field at a point 2 cm away from the centre. (b) A charge of 6×10−8C is placed on the hollow sphere. Find the surface charge density on the outer surface of the hollow sphere.
View SolutionCalculate the magnitude and direction of the electric field at a point P which is 30 cm to the right of a point charge Q=−3.0×10−6C
View SolutionThe electric force experienced by a charge of 5×10−6C is 25×10−3N. Find the magnitude of the electric field at that position of the charge due to the source charges.
View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.
 View Solution
View SolutionFind the electric field at point O, due to the segment of a ring, whose linear charge density is 8C/cm
 View Solution
View SolutionFind the flux of the electric field through a spherical surface of radius R due to a charge of 8.85×10−8C at the centre and another equal charge at a point 3R away from the centre (Given : ε0=8.85×10−12 units )
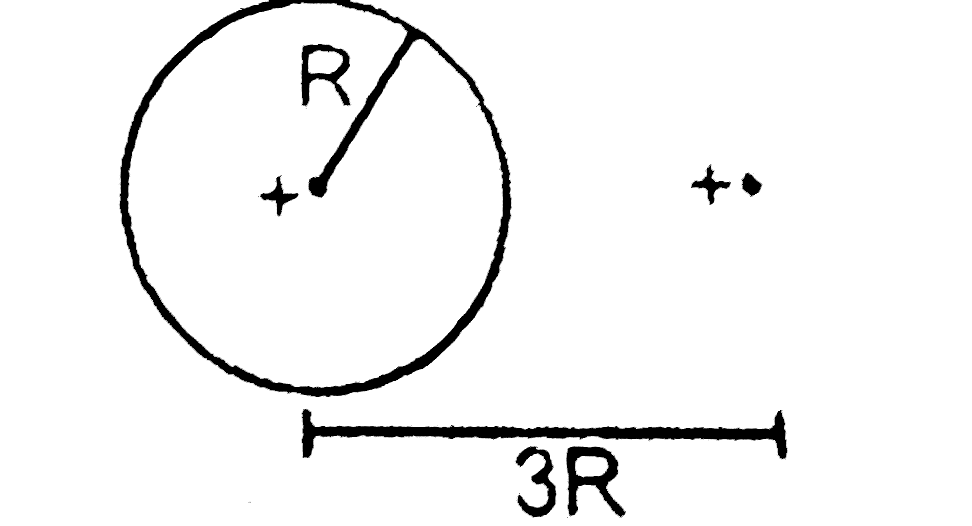 View Solution
View SolutionAn electric dipole consists of charges ±2.0×10−8C separated by a distance of 2.0×10−3 m. It is placed near a long line charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such that the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.
 View Solution
View SolutionAn electric dipole consists of charges ±2.0×108C separated by a distance of 2.0×10−3 m. It is placed near a long ilne charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such thet the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.
 View Solution
View SolutionFind the fluz f the electric field through a spherical surface of radius R due to a charge of 10−7C at the centre and another equal charge at a point 2R away from the centre (figure ).
 View Solution
View Solution

