A given charge is situated at a certain distance from an electric dipole in the end-on position experiences a force F If the distance of the charge is doubled, the force acting on the charge will be
2F
F2
F4
F8
The correct Answer is:4
To solve the problem, we need to analyze how the force acting on a charge due to an electric dipole changes when the distance from the dipole is altered. Here are the steps to derive the solution:
1. Understand the Initial Setup:
- We have an electric dipole and a charge placed at a distance R from the dipole in the end-on position. The force experienced by the charge at this distance is F.
2. Express the Force in Terms of Distance:
- The force F acting on the charge due to the dipole is inversely proportional to the cube of the distance from the dipole. This can be expressed as:
F∝1R3
- We can write this relationship as:
F=k⋅1R3
where k is a proportionality constant.
3. Change the Distance:
- Now, we double the distance from the dipole, so the new distance becomes R′=2R.
4. Calculate the New Force:
- The new force F′ acting on the charge at this new distance can be expressed similarly:
F′∝1(2R)3
- This simplifies to:
F′∝18R3
- We can write this as:
F′=k⋅1(2R)3=k⋅18R3
5. Relate the Two Forces:
- Now we can relate F′ to F:
F′=18⋅k⋅1R3=F8
6. Conclusion:
- Therefore, when the distance of the charge is doubled, the new force F′ acting on the charge will be:
F′=F8
Final Answer:
When the distance of the charge is doubled, the force acting on the charge will be F8.
- We have an electric dipole and a charge placed at a distance R from the dipole in the end-on position. The force experienced by the charge at this distance is F.
- The force F acting on the charge due to the dipole is inversely proportional to the cube of the distance from the dipole. This can be expressed as:
F∝1R3
- We can write this relationship as:
F=k⋅1R3
where k is a proportionality constant.
- Now, we double the distance from the dipole, so the new distance becomes R′=2R.
- The new force F′ acting on the charge at this new distance can be expressed similarly:
F′∝1(2R)3
- This simplifies to:
F′∝18R3
- We can write this as:
F′=k⋅1(2R)3=k⋅18R3
- Now we can relate F′ to F:
F′=18⋅k⋅1R3=F8
- Therefore, when the distance of the charge is doubled, the new force F′ acting on the charge will be:
F′=F8
When the distance of the charge is doubled, the force acting on the charge will be F8.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-B(OBJECTIVE TYPE QUESTION( ONLY ONE ANSWER)
12 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-C ( OBJECECTIVE TYPE QUESTIONS)
2 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - TRY YOURSELF
33 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
Similar Questions
Net charge on an electric dipole is ………….. .
View SolutionTwo charges of equal magnitudes and at a distance r exert a force F on each other. If the charges are halved and distance between them is doubled, then the new force acting on each charge is
View SolutionTwo large parallel metal carry charges +Q and –Q respectively . A test charge q0 placed between them experiences a force F. If the separation between the plants is doubled, then the force on the test charge will be
View SolutionAt a certain distance from a point charge, the field intensity is 500Vm and the potential is −3000V. The distance to the charge and the magnitude of the charge respectively are
View SolutionAt a certain distance from a point charge, the field intensity is 500V/m and the potential is −3000V. The distance to the charge and the magnitude of the charge respectively are
View SolutionAt a certain distance from a point charge, the field intensity is 500V/m and the potentil is −3000V. The distance to the charge and the magnitude of the charge respectively are
View Solutionfour charges are placed each at a distance from origin. the dipole moment of configuration is

View SolutionFigure shows a uniformly charged sphere of radius R and total charge Q. A point charge q is situated outside the sphere at a distance r from centre of sphere. Find out the following :
(i) Force acting on the point charge q due to the sphere.
(ii) Force acting on the sphere due to the point charge.

View Solution4 charges are placed each at a distance a from origin . The dipole moment of configuration is .
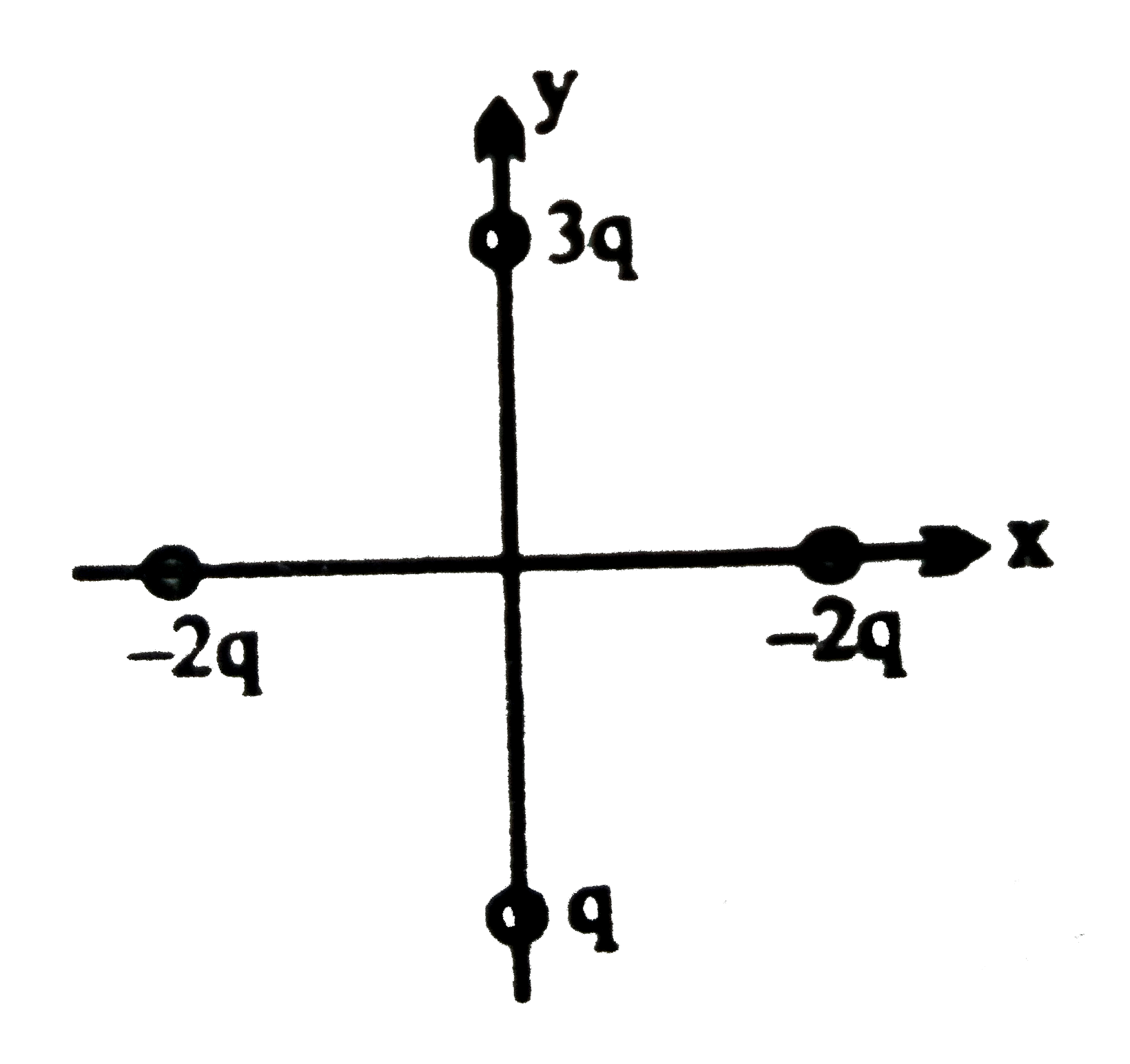 .
.
View SolutionA point negative charge -Q is placed at a distance r from a dipole with dipole moment P in the xy plane as shown in fig. The x-component of force acting on the charge-Q is
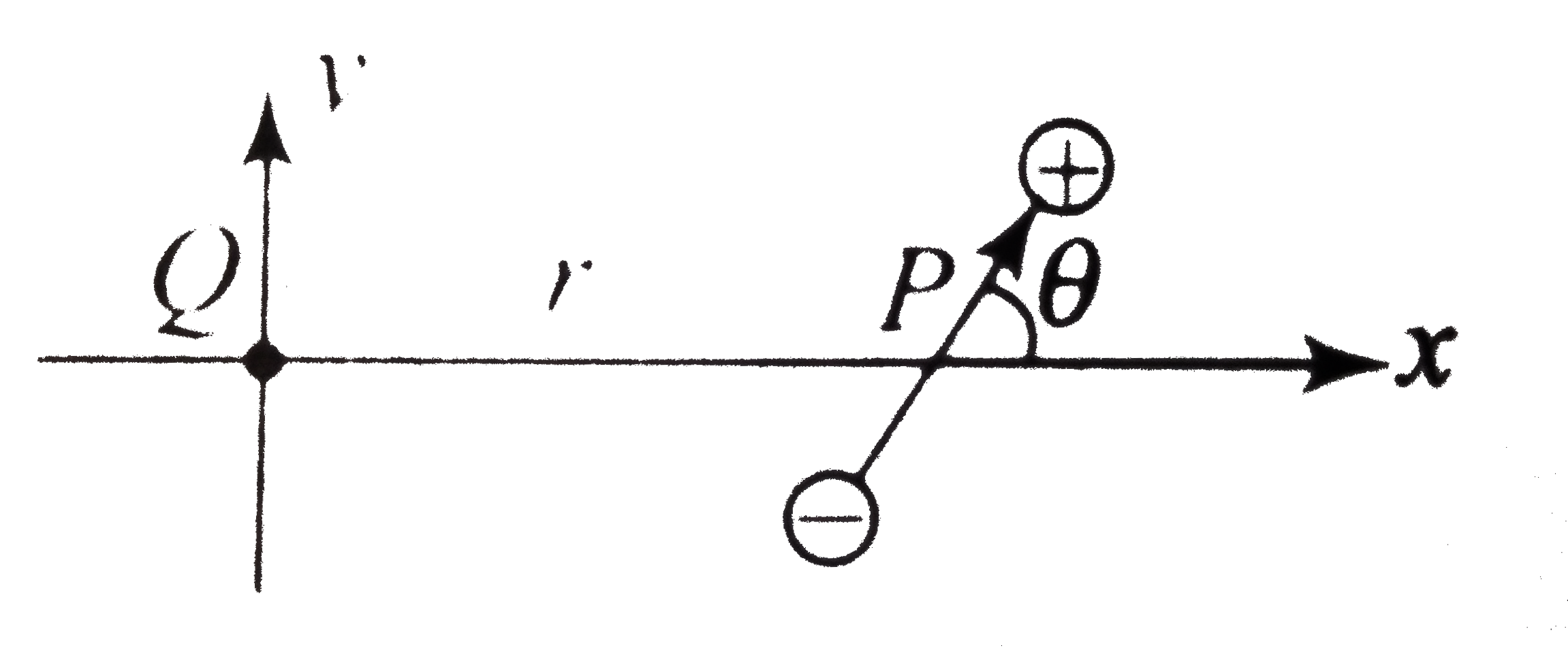
View Solution
