The application of Gauss's theorem gives rise to an easy evolution of electric field in the case of
A charged body of any geometrical configuration
A charged body of regular geometrical configuration
Revolving charged bodies
Charges forming dipoles
The correct Answer is:2
To solve the question regarding the application of Gauss's theorem and its ease of evaluating the electric field for different geometrical configurations, we can follow these steps:
Step 1: Understand Gauss's Theorem
Gauss's theorem states that the electric flux (Φ) through a closed surface is equal to the charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀):
Φ=Qϵ0
Step 2: Relate Electric Field to Flux
The electric flux can also be expressed in terms of the electric field (E) and the surface area (S) of the closed surface:
Φ=E⋅S
Where E is the electric field and S is the surface area through which the field lines pass.
Step 3: Combine the Two Equations
By combining the two equations from Steps 1 and 2, we can express the electric field as:
E⋅S=Qϵ0
From this, we can derive the electric field:
E=Qϵ0⋅S
Step 4: Analyze Geometrical Configurations
Now, we need to evaluate the types of geometrical configurations for which we can easily determine the surface area (S):
- For irregular shapes: Determining the surface area is complex and often not straightforward.
- For regular geometrical shapes (like spheres, cylinders, and cubes): The surface area can be calculated easily using standard formulas.
Step 5: Conclusion
Since Gauss's theorem allows for straightforward evaluation of the electric field primarily in cases where the surface area can be easily calculated, the best option is:
- Charged body of regular geometrical configuration (like spheres, cylinders, or cubes).
Thus, the answer to the question is that the application of Gauss's theorem gives rise to an easy evaluation of electric field in the case of a charged body of regular geometrical configuration.
Final Answer
The correct option is: Charged body of regular geometrical configuration.
---
Gauss's theorem states that the electric flux (Φ) through a closed surface is equal to the charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀):
Φ=Qϵ0
The electric flux can also be expressed in terms of the electric field (E) and the surface area (S) of the closed surface:
Φ=E⋅S
Where E is the electric field and S is the surface area through which the field lines pass.
By combining the two equations from Steps 1 and 2, we can express the electric field as:
E⋅S=Qϵ0
From this, we can derive the electric field:
E=Qϵ0⋅S
Now, we need to evaluate the types of geometrical configurations for which we can easily determine the surface area (S):
- For irregular shapes: Determining the surface area is complex and often not straightforward.
- For regular geometrical shapes (like spheres, cylinders, and cubes): The surface area can be calculated easily using standard formulas.
Since Gauss's theorem allows for straightforward evaluation of the electric field primarily in cases where the surface area can be easily calculated, the best option is:
- Charged body of regular geometrical configuration (like spheres, cylinders, or cubes).
The correct option is: Charged body of regular geometrical configuration.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-B(OBJECTIVE TYPE QUESTION( ONLY ONE ANSWER)
12 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-C ( OBJECECTIVE TYPE QUESTIONS)
2 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - TRY YOURSELF
33 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
Similar Questions
State Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View SolutionAssertion: In case of charged spherical shells, E-r graph is discontinuous while V-r graph is continuous
Reason: According to Gauss's theorem only the charge inside a closed surface can produce electric field at some point.
View Solution
Knowledge Check
Assertion: In case of charged spherical shells, E-r graph is discontinuous while V-r graph is continuous
Reason: According to Gauss's theorem only the charge inside a closed surface ca produce electric field at some point.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
In case of infinite long wire electric field is proportional to
View SolutionFigure shows two concentric shells of radii a and b uniformly distributed charges q and -q. Which of the following graphs gives correct variation of electric field intensity E with the distance r from the centre?

View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angle to the strip.
(a) Calculate the drift velocity vd of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field E Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field EH across the conductor until the forces of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field EH?
Assume that n, the number of conductor electrons per unit volume is 1.1×1029m−3,h=0.02m,w=0.1cm,i=50A,andB=2T.

View SolutionAssertion : With the help of Gauss's theorm we can find electric field at any point.
Reason : Gauss's theorem can be applied for any type of charge distribution.
View SolutionUsing Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View SolutionUsing Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View SolutionThe figure here gives the electric field of an EM wave at a certain point and a certain. The wave is transporting energy in the negative z direction. What is the direction of the magnetic field of the wave at the point and instant?
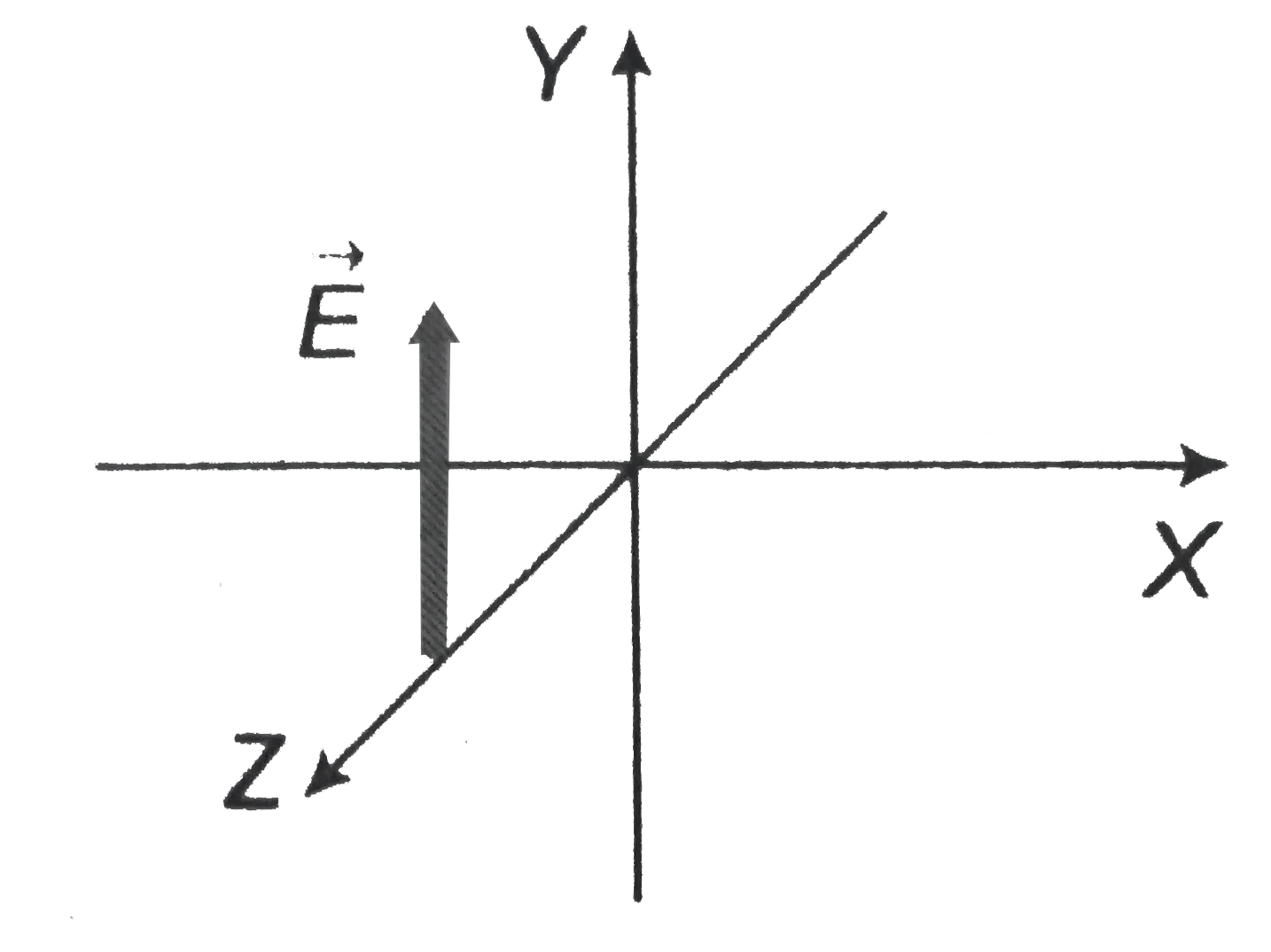
A. Towards + X direction
B. Towards - X direction
C. Towards + direction
D. Towards - Z direction
View Solution
