For the following arrangement, find the equivalent capacitance between A and B
 .
.
Video Solution
Text Solution
Here, the 3μF,4μF and 5μF capacitors are in series.
∴Ceq=(13+14+15)−1=6012+20+15=6047μF
Now, 2μF and 6047 are in parallel , so we have
Ceq=C1+C2=15447μF
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE20videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A44videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)15videos
GRAVITATION
Similar Questions
Find the equivalent capacitance between C and B.
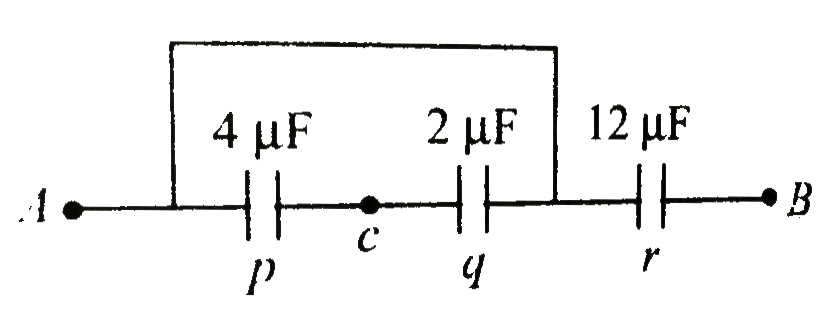 View Solution
View SolutionThe equivalent capacitance between A and B is
 View Solution
View SolutionThe equivalent capacitance between A and B is
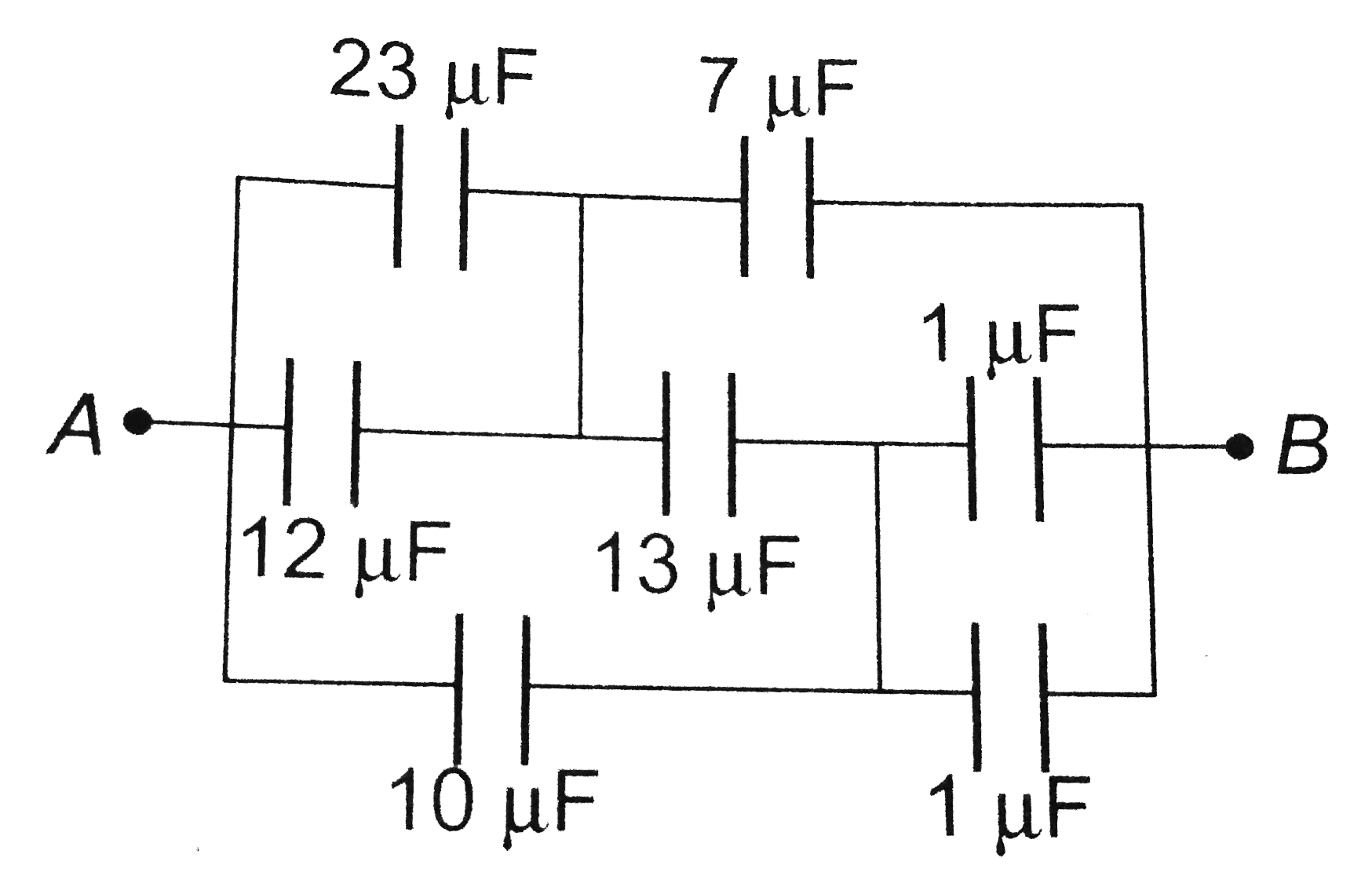 View Solution
View SolutionEquivalent capacitance between A and B is
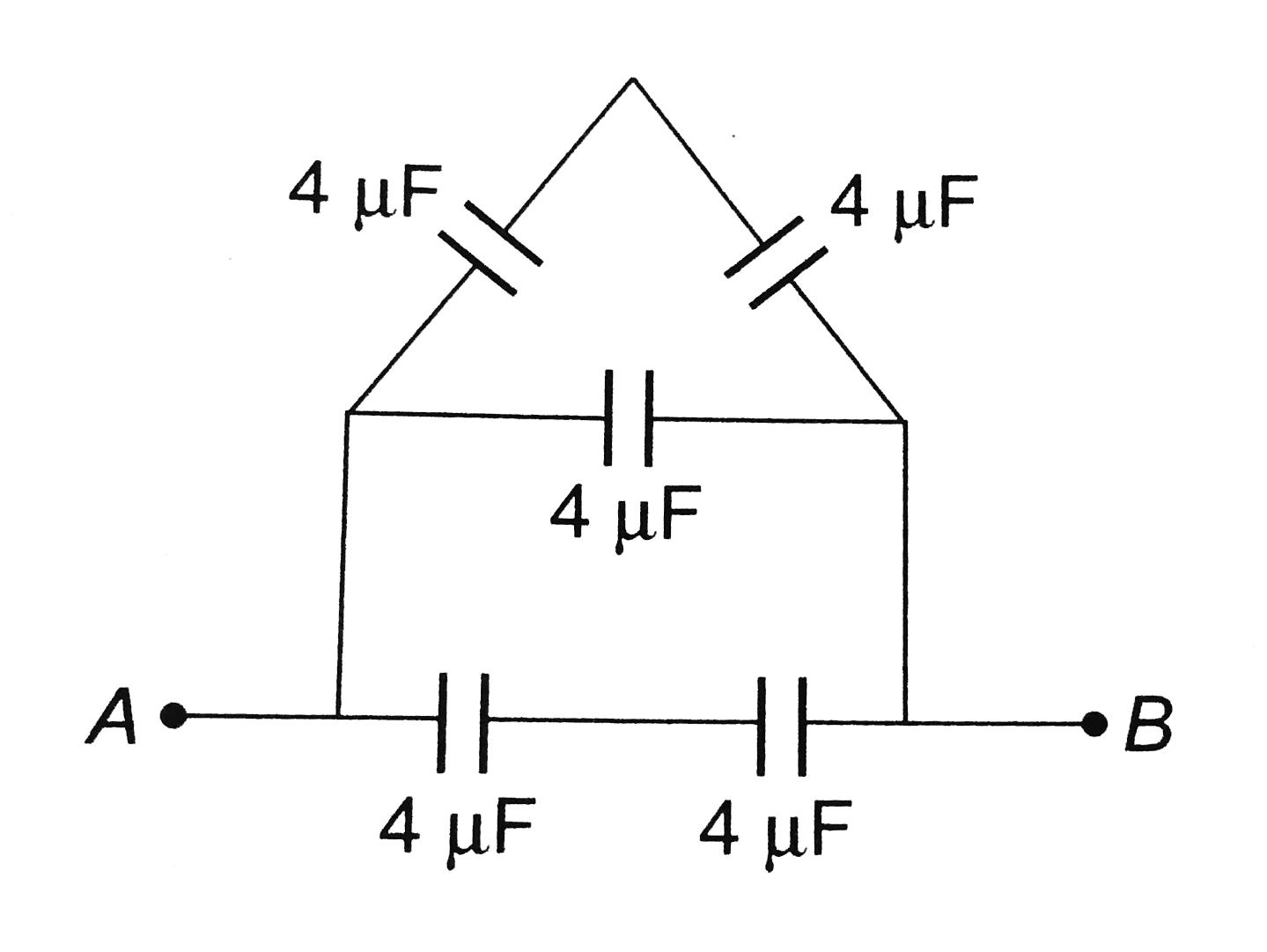 View Solution
View SolutionFind out equivalent capacitance between A and B.
 View Solution
View SolutionEquivalent capacitance between A and B is:
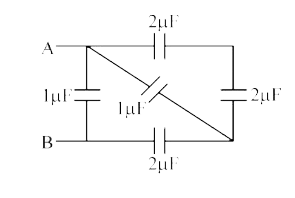 View Solution
View SolutionFind equivalent capacitance between A and B
 View Solution
View SolutionFind the equivalent capacitance between point A and B .
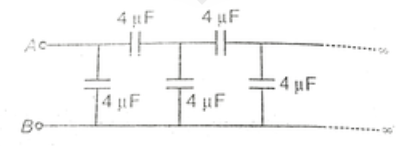 View Solution
View SolutionThe equivalent capacitance between A and B will be
View SolutionThe equivalent capacitance between X and Y is
 View Solution
View Solution

