A point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
Remember that the superposition principle is valid even in the presence of conducors.

'q' alone would produce an electric field at all points within the volume of the conductor . The conductor must some how cancel the field due to q at all points interior to it. But there is no charge given to the conductor. The conductor solves this problem in a remarkable way. It pulls out positive and negative charges of equal magnitude from its volume and spreads them on its surface in such a manner that at every point in its interior the field due to q is cancelled by the field due to the surface charges. The potential ϕ within the sphere is uniform, because it is a conducting sphere. If we can find the value of ϕ at any point in the sphere, our problem is solved . Of all points within the sphere, there is one point which is best suited from the calculation of ϕ . This point is the centre C of the sphere . Every element of the surface is at the same distance 'a' from the centre of the sphere and , therefore, the potential at C due to all the surface charges ( irrespective of their distribution ) is
∮σ.ds4πε0a=14πε0a∮σ.ds=0
Because the total charge on the surface of the sphere is zero in this problem. So only contribution to potential at C comes from q now, and this is equal to q4πε0R
Thus the potential of the sphere is q4πε0R
Note that the above discussion can be extended to the case where the net charge on the spherical has any given value Q . Several point charges outside the conductor can also be taken into account.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE20videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A44videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)15videos
GRAVITATION
Similar Questions
A point charge Q is situated (outside) at a distance r from the centre of an uncharged conducting solid sphere of radius R. The potential due to induced charges (on the conductor) at a point B inside the conductor whose distance form the point charge is d is ______
View SolutionA point charge q , is placed at a distance r from the centre of an aluminium sphere, of radius R (r>R) . Selectr the correct alternatives.
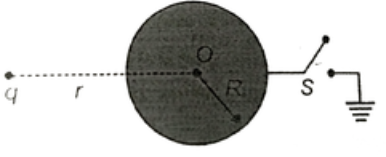 View Solution
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
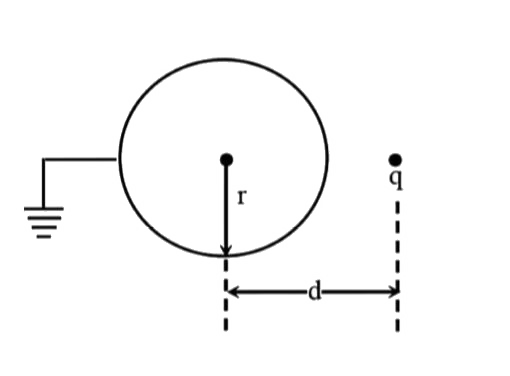 View Solution
View Solution
A point charge q'q is placed at distance 'a' from the centre of an uncharged thin spherical conducting shell of radius R=2a. A point 'P' is located at a distance 4a from the centre of the conducting shell as shown. The electric potential due to induced charge on the inner surface of the conducting shell at point 'P' isView SolutionA charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be
 View Solution
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R.The distance r<R.The electric potential at the centre of the shell will be
 View Solution
View SolutionA point charge +Q is placed at point B at a distance 2R from the center O of an uncharged thin conducting shell of radius R as shown in figure. If VA be the potential at point A, which is at a radial distance of R/2 from the center of the shell, then
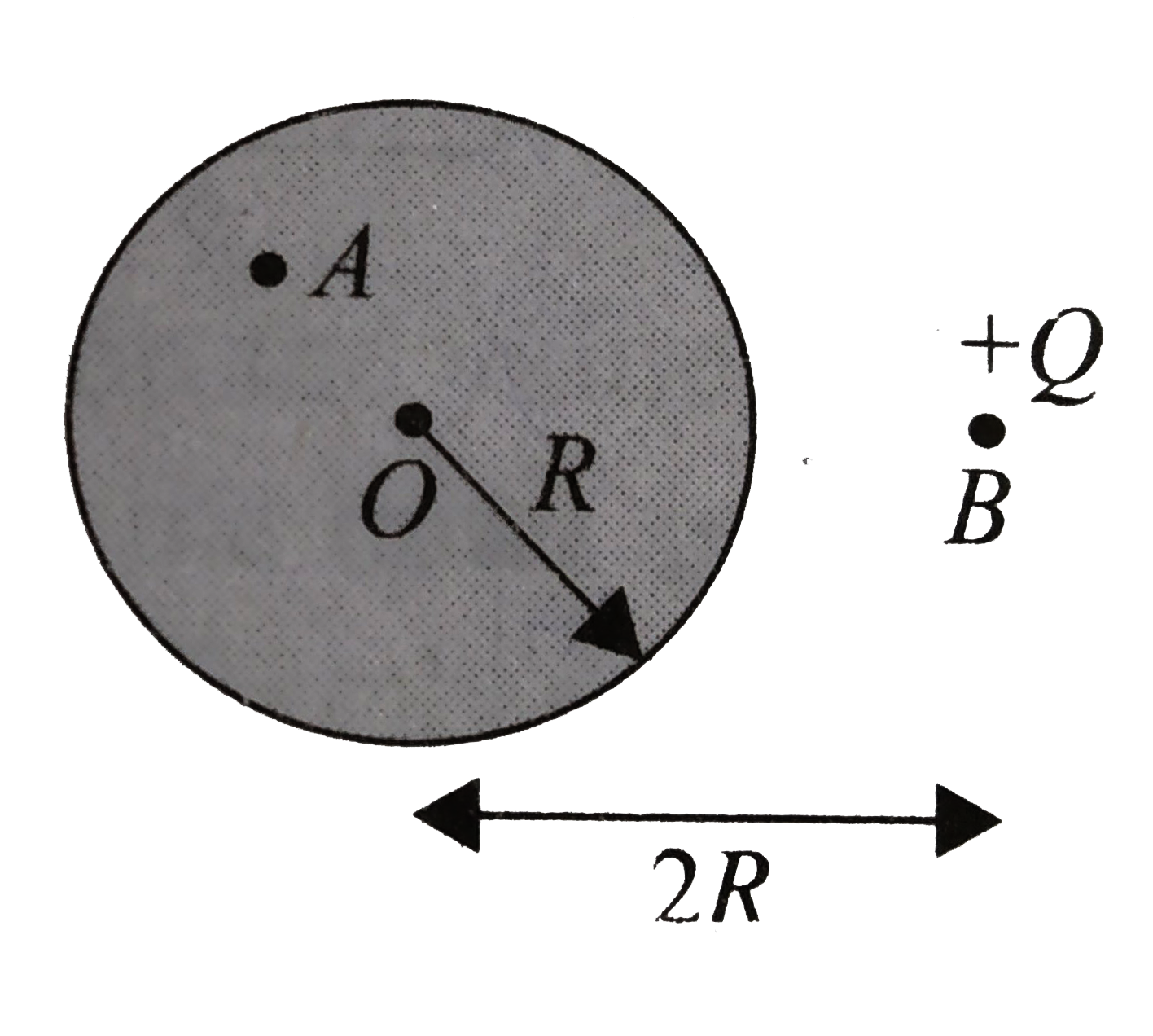 View Solution
View SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
The potential of outer shell isView SolutionA solid conducting sphere of radius 'a' is surrounded by a thin uncharged concentric conducting shell of radius 2a. A point charge q is placed at a distance 4a from common centre of conducting sphere and shell. The inner sphere is then grounded
The charge on solid sphere isView Solution

