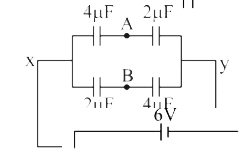
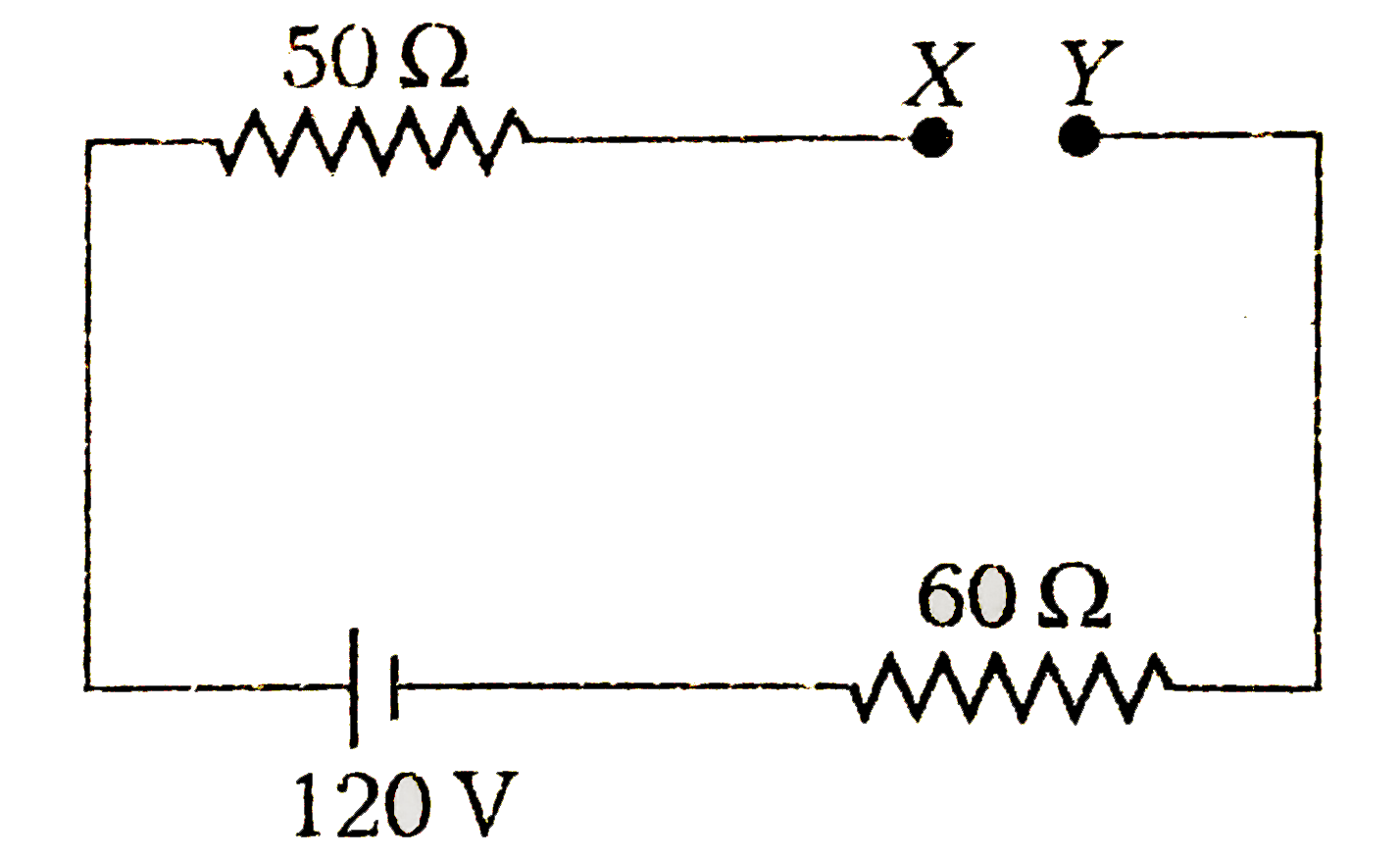Consider the electrical circuit shown.A potential difference V exists between A and B. The charges on various capacitors are shown. Select the correct relationship (s) .
q1=q2
q3=q4
q1=q3+q4
q3=q42
The correct Answer is:(1,3,4)
To solve the problem, we need to analyze the given electric circuit with capacitors and the relationships between the charges on them. Here’s a step-by-step breakdown:
Step 1: Understand the Circuit Configuration
We have a circuit with capacitors connected between points A and B. The charges on the capacitors are denoted as q1,q2,q3,q4, etc. Capacitors in series have the same charge, while capacitors in parallel have the same voltage across them.
Hint: Identify which capacitors are in series and which are in parallel.
Step 2: Identify Relationships in Series Capacitors
For capacitors in series, the charge on each capacitor is the same. Therefore, we can write:
q1=q2
Hint: Remember that in series, the charge remains constant across each capacitor.
Step 3: Analyze the Parallel Capacitors
In the circuit, we have capacitors that are in parallel. The total charge on the capacitors in parallel is the sum of the individual charges. If q1 is the charge on the first capacitor and q3 and q4 are the charges on the parallel capacitors, we can write:
q1=q3+q4
Hint: For parallel capacitors, the total charge is the sum of the individual charges.
Step 4: Relate Charges Using Capacitance
Using the relationship Q=C⋅V, we can express the potential differences across the capacitors. For the upper branch with capacitors of capacitance 3C:
Vxy=q33C
For the lower branch with capacitance 2C:
Vxy=q42C
Hint: Use the formula Q=C⋅V to relate charge and voltage.
Step 5: Set the Voltage Equations Equal
Since the potential difference across both branches must be equal, we can set the equations from Step 4 equal to each other:
q33C=q42C
Hint: Equating the voltages gives us a relationship between the charges.
Step 6: Solve for One Charge in Terms of Another
From the equation q33C=q42C, we can simplify and solve for q3:
q3=32q4
Hint: Rearranging the equation helps to express one variable in terms of another.
Step 7: Compile the Relationships
From the analysis, we have established the following relationships:
1. q1=q2
2. q1=q3+q4
3. q3=32q4
Conclusion
Based on the relationships derived:
- q1=q2 (True)
- q1=q3+q4 (True)
- q3=32q4 (True)
Thus, the correct relationships are:
- Q1=Q2
- Q1=Q3+Q4
- Q3=32Q4
Final Answer
The correct options are A, C, and D.
We have a circuit with capacitors connected between points A and B. The charges on the capacitors are denoted as q1,q2,q3,q4, etc. Capacitors in series have the same charge, while capacitors in parallel have the same voltage across them.
For capacitors in series, the charge on each capacitor is the same. Therefore, we can write:
q1=q2
In the circuit, we have capacitors that are in parallel. The total charge on the capacitors in parallel is the sum of the individual charges. If q1 is the charge on the first capacitor and q3 and q4 are the charges on the parallel capacitors, we can write:
q1=q3+q4
Using the relationship Q=C⋅V, we can express the potential differences across the capacitors. For the upper branch with capacitors of capacitance 3C:
Vxy=q33C
For the lower branch with capacitance 2C:
Vxy=q42C
Since the potential difference across both branches must be equal, we can set the equations from Step 4 equal to each other:
q33C=q42C
From the equation q33C=q42C, we can simplify and solve for q3:
q3=32q4
From the analysis, we have established the following relationships:
1. q1=q2
2. q1=q3+q4
3. q3=32q4
Based on the relationships derived:
- q1=q2 (True)
- q1=q3+q4 (True)
- q3=32q4 (True)
- Q1=Q2
- Q1=Q3+Q4
- Q3=32Q4
The correct options are A, C, and D.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-D(COMPREHENSION-I)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - COMPREHENSION-II
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B(OBJECTIVE TYPE QUESTIONS(ONLY ONE ANSWER) )
29 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Knowledge Check
The potential difference between A and B as shown in figure is
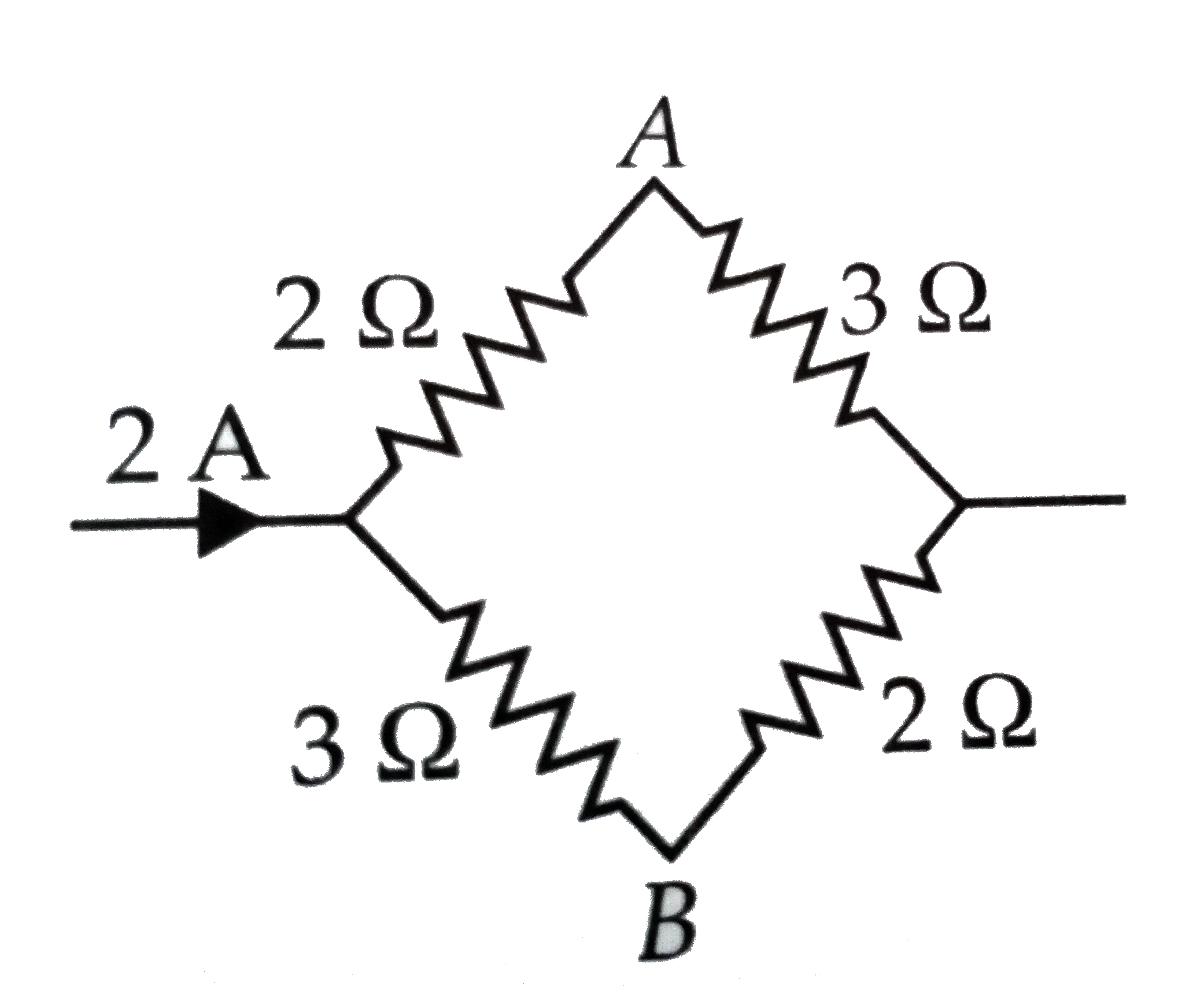 A1VB2VC3VD4V
A1VB2VC3VD4V
In the circuit shown, the potential difference between x and y will be
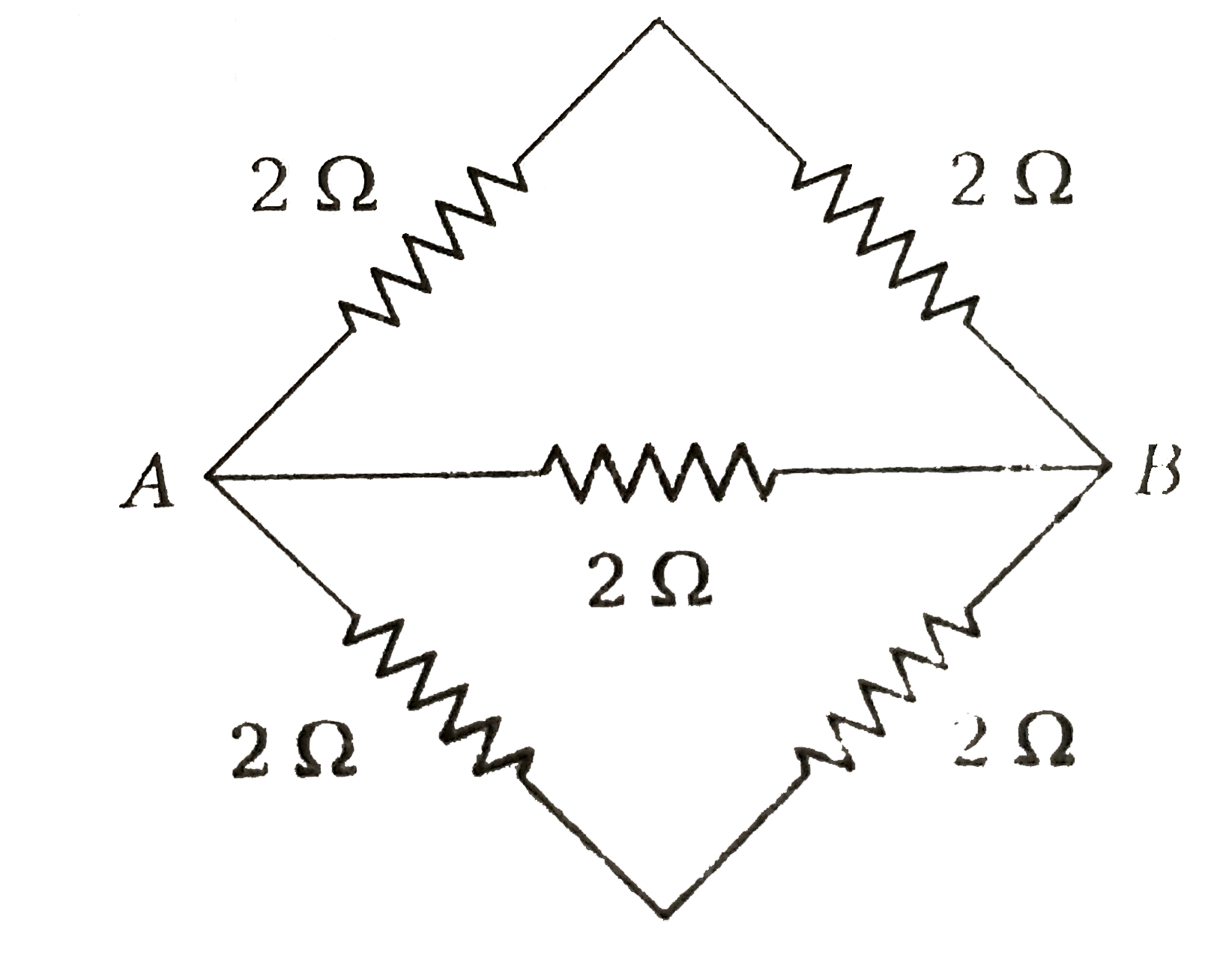
View SolutionIn the circuit shown, what is the potential different VPQ ?
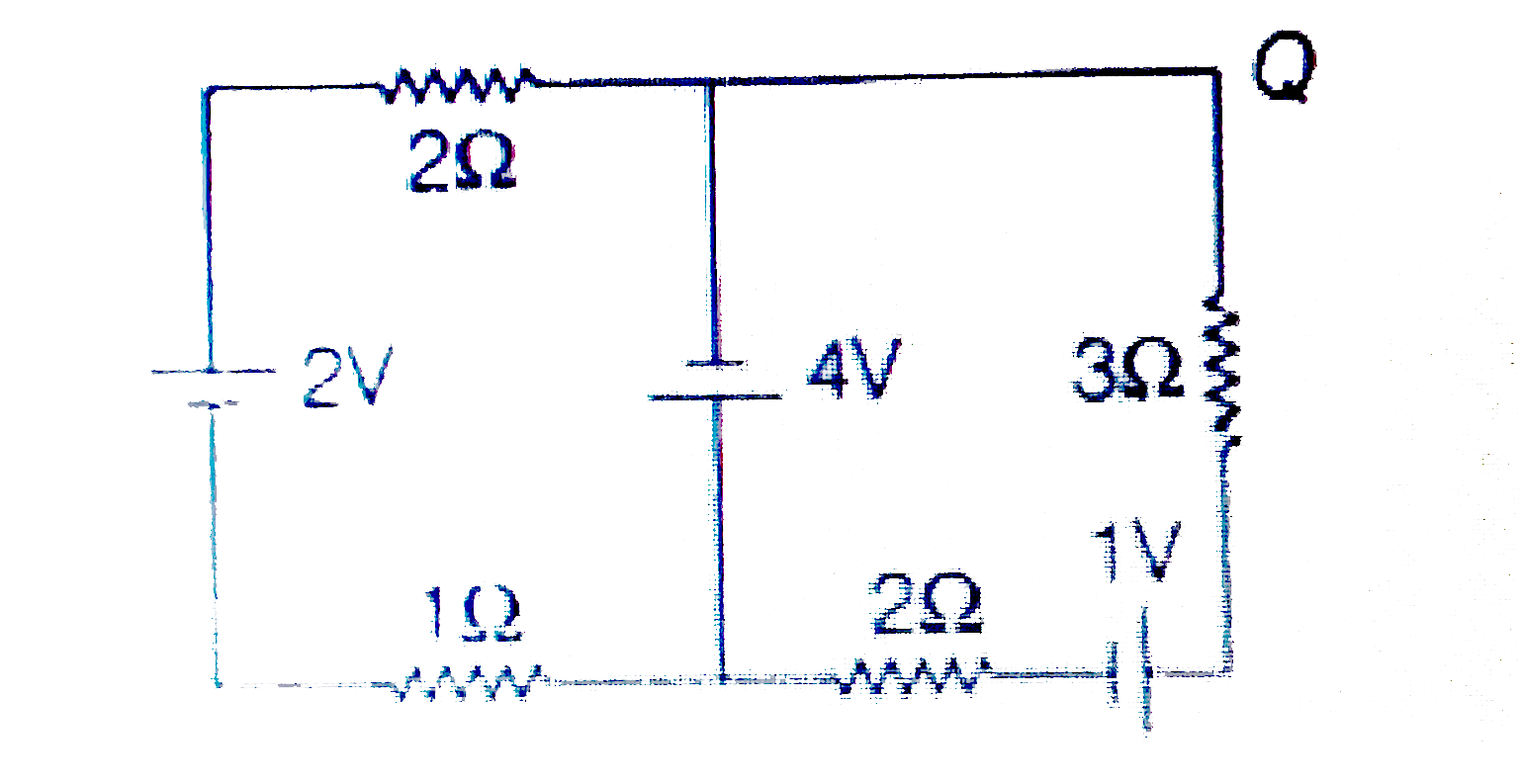
View SolutionFind the potential difference between A and B as shown in the figure
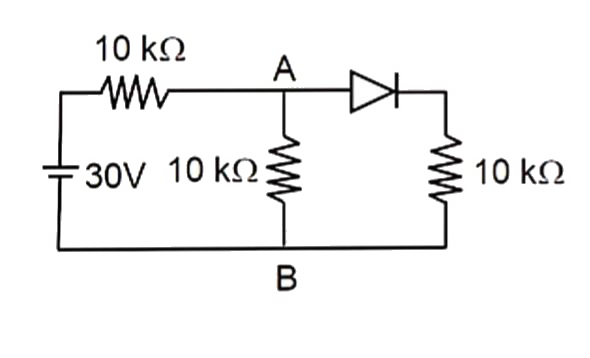
View SolutionIn the circuit shown, the potential difference between A and B VAandVB is equal to_______V.
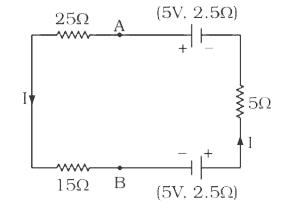
View SolutionWhat is the potential difference between points A and B in the circuit shown?
View SolutionIn the circuit shown, what is the potential difference VPQ in volts ?

View SolutionIn the given circuit , the potential difference between A and B is 18 V and charge on 2 μF capacitor is 24 μ C . The value of C is

View Solution