A particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
The potential energy of the system of particles P and Q, at closest separation is
14πε0q2r+12mv20
−14πε0q2r+12mv20
14πε0q2r+mv204
−14πε0q2r+mv204
The correct Answer is:3
To find the potential energy of the system of particles P and Q at their closest separation, we can follow these steps:
1. Understand the System:
- We have two particles, P and Q, both with charge q and mass m.
- Particle Q is projected towards P with an initial speed v0 from a distance r.
2. Identify Closest Approach:
- At the closest approach, the distance between P and Q is minimized. At this point, both particles will have the same velocity because the rate of change of distance between them is zero.
3. Conservation of Momentum:
- The initial momentum of the system is given by the momentum of Q since P is stationary:
pinitial=mv0
- At the closest approach, let the common velocity of both particles be v′. The total momentum at this point is:
pfinal=2mv′
- By conservation of momentum:
mv0=2mv′
- Solving for v′:
v′=v02
4. Conservation of Mechanical Energy:
- The initial mechanical energy consists of the kinetic energy of Q and the potential energy due to the separation r:
Einitial=12mv20+kq2r
- At the closest approach, the kinetic energy of both particles and the potential energy at the closest distance d (which we need to find) is:
Efinal=2⋅12mv′2+Ufinal=12m(v02)2+Ufinal
- This simplifies to:
Efinal=12mv204+Ufinal=mv208+Ufinal
5. Equating Initial and Final Energies:
- Setting the initial energy equal to the final energy:
12mv20+kq2r=mv208+Ufinal
- Rearranging gives:
Ufinal=12mv20+kq2r−mv208
- Simplifying further:
Ufinal=4mv208−mv208+kq2r=3mv208+kq2r
6. Final Expression:
- Therefore, the potential energy of the system at the closest separation is:
Ufinal=3mv208+kq2d
- Here, d is the closest distance between the two charges.
- We have two particles, P and Q, both with charge q and mass m.
- Particle Q is projected towards P with an initial speed v0 from a distance r.
- At the closest approach, the distance between P and Q is minimized. At this point, both particles will have the same velocity because the rate of change of distance between them is zero.
- The initial momentum of the system is given by the momentum of Q since P is stationary:
pinitial=mv0
- At the closest approach, let the common velocity of both particles be v′. The total momentum at this point is:
pfinal=2mv′
- By conservation of momentum:
mv0=2mv′
- Solving for v′:
v′=v02
- The initial mechanical energy consists of the kinetic energy of Q and the potential energy due to the separation r:
Einitial=12mv20+kq2r
- At the closest approach, the kinetic energy of both particles and the potential energy at the closest distance d (which we need to find) is:
Efinal=2⋅12mv′2+Ufinal=12m(v02)2+Ufinal
- This simplifies to:
Efinal=12mv204+Ufinal=mv208+Ufinal
- Setting the initial energy equal to the final energy:
12mv20+kq2r=mv208+Ufinal
- Rearranging gives:
Ufinal=12mv20+kq2r−mv208
- Simplifying further:
Ufinal=4mv208−mv208+kq2r=3mv208+kq2r
- Therefore, the potential energy of the system at the closest separation is:
Ufinal=3mv208+kq2d
- Here, d is the closest distance between the two charges.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - COMPREHENSION-II
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-E (Assertion-Reason Type Questios)
12 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS (More than one answer))
13 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
A particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
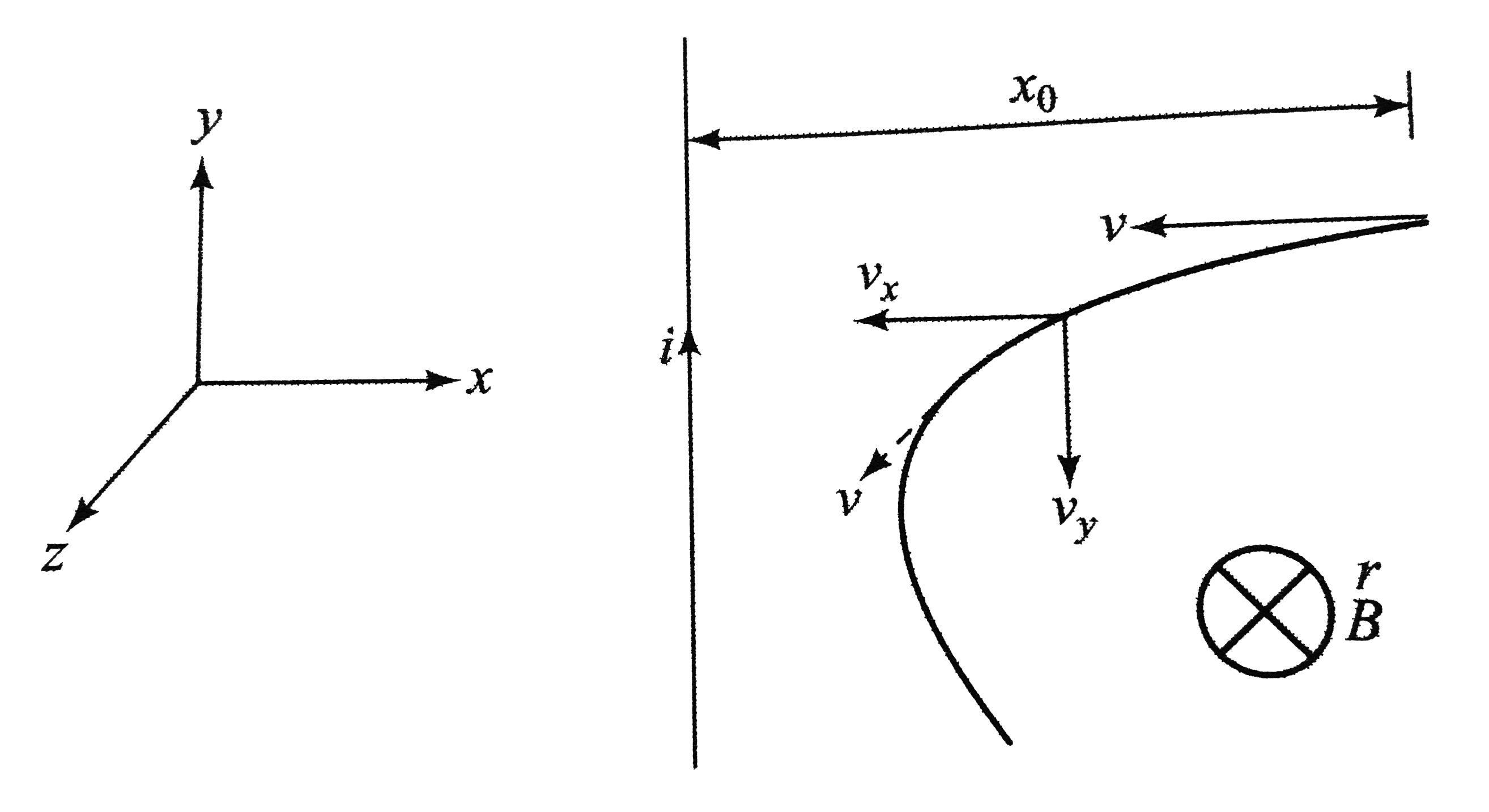
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View SolutionA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionA charged particle of charge 'Q' is held fixed and another charged particle of mass 'm' and charge 'q' (of the same sign) is released from a distance 'r'. The impulse of the force exerted by the external agent on the fixed charge by the time distance between 'Q' and 'q' becomes 2r is
View SolutionThe displacement-time graphs of two particles P and Q are as shown in the figure. The ratio of their velocities VP and VQ will be
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View Solution
