STATEMENT-1: If potential energy of a dipole in stable equilibrium position is zero, its potential energy is unstable equilibrium position will be 2pE, where p and E represent the dipole moment and electric field respectively
and
STATEMENT-2 : The potential energy of a dipole is minimum in stable equilibruim position and maximum in unstable equilibrium position.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False , Statement-2 is True
The correct Answer is:B
To solve the problem, we need to analyze the two statements provided regarding the potential energy of a dipole in electric fields.
1. Understanding Stable and Unstable Equilibrium:
- In a stable equilibrium position, the dipole aligns with the electric field. The potential energy (U) in this position is given by:
U=−→p⋅→E=−pEcos(0)=−pE
- In an unstable equilibrium position, the dipole is oriented opposite to the electric field. The potential energy in this position is:
U=−→p⋅→E=−pEcos(180∘)=pE
2. Calculating the Difference in Potential Energy:
- If we assume that the potential energy in stable equilibrium is zero (U_stable = 0), then we can express the potential energy in unstable equilibrium as:
Uunstable=Uunstable−Ustable=pE−(−pE)=pE+pE=2pE
- Thus, if the potential energy in stable equilibrium is zero, the potential energy in unstable equilibrium will indeed be 2pE.
3. Analyzing Statement 1:
- Statement 1 claims that if the potential energy of a dipole in stable equilibrium is zero, then its potential energy in unstable equilibrium will be 2pE. This statement is true based on our calculations.
4. Analyzing Statement 2:
- Statement 2 states that the potential energy of a dipole is minimum in stable equilibrium and maximum in unstable equilibrium.
- From our calculations, we see that in stable equilibrium, the potential energy is −pE (which is indeed a minimum), and in unstable equilibrium, it is pE (which is indeed a maximum). Therefore, this statement is also true.
5. Determining the Relationship Between the Statements:
- While both statements are true, Statement 2 does not provide a correct explanation for Statement 1. Statement 1 is a specific condition regarding potential energies, while Statement 2 is a general observation about the nature of potential energy in dipoles.
Conclusion:
- Statement 1 is true.
- Statement 2 is true.
- Statement 2 does not correctly explain Statement 1.
Thus, the final answer is that both statements are true, but Statement 2 is not a correct explanation for Statement 1.
- In a stable equilibrium position, the dipole aligns with the electric field. The potential energy (U) in this position is given by:
U=−→p⋅→E=−pEcos(0)=−pE
- In an unstable equilibrium position, the dipole is oriented opposite to the electric field. The potential energy in this position is:
U=−→p⋅→E=−pEcos(180∘)=pE
- If we assume that the potential energy in stable equilibrium is zero (U_stable = 0), then we can express the potential energy in unstable equilibrium as:
Uunstable=Uunstable−Ustable=pE−(−pE)=pE+pE=2pE
- Thus, if the potential energy in stable equilibrium is zero, the potential energy in unstable equilibrium will indeed be 2pE.
- Statement 1 claims that if the potential energy of a dipole in stable equilibrium is zero, then its potential energy in unstable equilibrium will be 2pE. This statement is true based on our calculations.
- Statement 2 states that the potential energy of a dipole is minimum in stable equilibrium and maximum in unstable equilibrium.
- From our calculations, we see that in stable equilibrium, the potential energy is −pE (which is indeed a minimum), and in unstable equilibrium, it is pE (which is indeed a maximum). Therefore, this statement is also true.
- While both statements are true, Statement 2 does not provide a correct explanation for Statement 1. Statement 1 is a specific condition regarding potential energies, while Statement 2 is a general observation about the nature of potential energy in dipoles.
- Statement 1 is true.
- Statement 2 is true.
- Statement 2 does not correctly explain Statement 1.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-F(MATRIX-MATCH TYPE QUESTIONS)
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-G(INTEGER ANSWER TYPE QUESTIONS)
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - COMPREHENSION-II
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
For the potential energy function shown in fig. there will be an unstable equilibrium at position

View SolutionAssertion :Mean positon of SHM is the stable equlibrium position.
Reason: In stable equilibrium , position potential energy is minimum.
View SolutionPotential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
View SolutionPotential energy of a particle is related to x coordinate by equation x2−2x . Particle will be in stable equilibrium at :
View SolutionThe work done in rotating a bar magnet of magnetic moment M from its unstable equilibrium position to its stable equilibrium position in a uniform magnetic field B is
View SolutionPotential energy of a particle at position x is given by U=(x2−4x)J. Which of the following is equilibrium position of the particle?
View SolutionWhat is work done on dipole to rotate it form stable equilibrium position (θ1=0∘) to unstable equilibrium (θ2=180∘) ?
View SolutionA bar magnet of magnetic dipole moment 10Am2 is in stable equilibrium . If it is rotated through 30∘ , find its potential energy in new position [Given , B = 0.2 T]
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

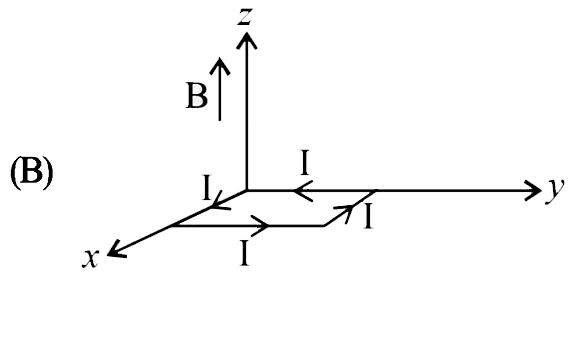

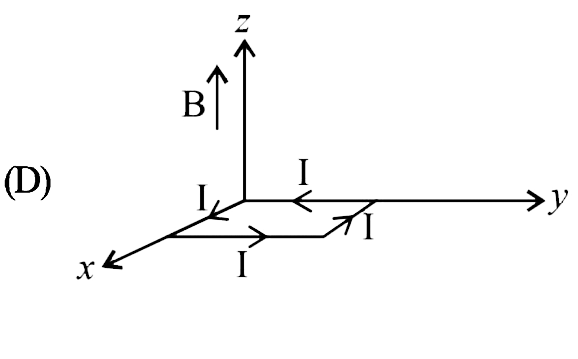
View SolutionAt what angle of electric dipole moment with uniform electric field, potential energy is maximum ?
View Solution
