What is the relationship between potential difference across the terminalsof a cell and emf of the cell?
To find the relationship between the potential difference across the terminals of a cell and the EMF (electromotive force) of the cell, we can analyze the situation using Kirchhoff's voltage law and consider different scenarios based on the current flowing through the cell.
1. Define the Cell and Parameters:
- Let the EMF of the cell be denoted as ϵ.
- Let the internal resistance of the cell be denoted as r.
- Let the current flowing through the circuit be denoted as I.
2. Apply Kirchhoff's Voltage Law:
- According to Kirchhoff's law, the sum of the potential differences (voltage) around a closed loop must equal zero.
- For our cell, we can express this as:
Va+ϵ−I⋅r=Vb
- Here, Va is the voltage at one terminal and Vb is the voltage at the other terminal.
3. Calculate the Potential Difference:
- Rearranging the equation gives us the potential difference V across the terminals:
Vb−Va=ϵ−I⋅r
- Thus, the potential difference V can be expressed as:
V=ϵ−I⋅r
4. Analyze Different Cases:
- Case 1: When no current flows (I=0):
V=ϵ−0⋅r=ϵ
- The potential difference equals the EMF.
- Case 2: When current flows in the same direction (I>0):
V=ϵ−I⋅r
- The potential difference is less than the EMF due to the voltage drop across the internal resistance.
- Case 3: When current flows in the opposite direction (I<0):
V=ϵ−(−I)⋅r=ϵ+I⋅r
- The potential difference is greater than the EMF, indicating that the battery is being charged.
5. Conclusion:
- The relationship between the potential difference V across the terminals of the cell and the EMF ϵ is given by:
V=ϵ−I⋅r
- This indicates that the potential difference depends on the current flowing through the cell and its internal resistance.
- Let the EMF of the cell be denoted as ϵ.
- Let the internal resistance of the cell be denoted as r.
- Let the current flowing through the circuit be denoted as I.
- According to Kirchhoff's law, the sum of the potential differences (voltage) around a closed loop must equal zero.
- For our cell, we can express this as:
Va+ϵ−I⋅r=Vb
- Here, Va is the voltage at one terminal and Vb is the voltage at the other terminal.
- Rearranging the equation gives us the potential difference V across the terminals:
Vb−Va=ϵ−I⋅r
- Thus, the potential difference V can be expressed as:
V=ϵ−I⋅r
- Case 1: When no current flows (I=0):
V=ϵ−0⋅r=ϵ
- The potential difference equals the EMF.
- Case 2: When current flows in the same direction (I>0):
V=ϵ−I⋅r
- The potential difference is less than the EMF due to the voltage drop across the internal resistance.
V=ϵ−(−I)⋅r=ϵ+I⋅r
- The potential difference is greater than the EMF, indicating that the battery is being charged.
- The relationship between the potential difference V across the terminals of the cell and the EMF ϵ is given by:
V=ϵ−I⋅r
- This indicates that the potential difference depends on the current flowing through the cell and its internal resistance.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
69 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
What is the relationship between potential difference across the terminals of a cell and emf of the cell ?
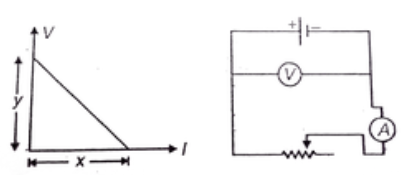
View SolutionFor a cell, the graph between the potential difference (V) across the terminals of the cells and the current I drawn from the cell is as shown in figure. Calculate the e.m.f. and the internal resistance of the cell.

View SolutionFor a cell, a graph is plotted between the potential difference V across the terminals of the cell and the current I drawn the cell. The emf and the internal resistance of the cell are E and r, respectively. Then
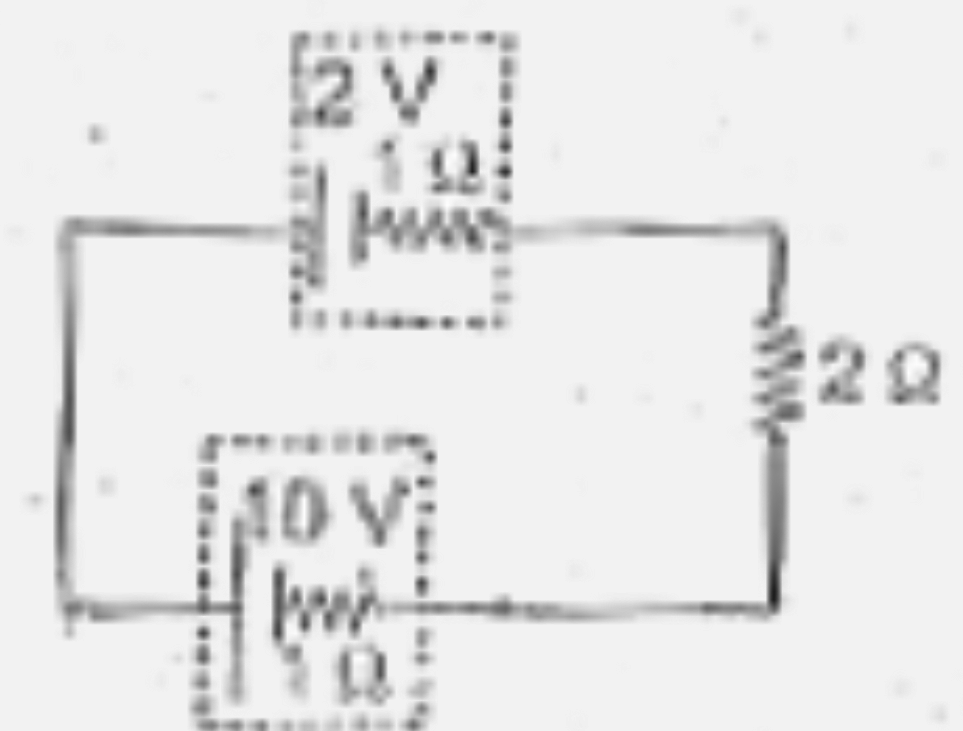
View SolutionIn the situation shown , the potential difference across the cell of smaller e.m.f is .
View SolutionA cell of e.m.f. 2V and internal resistance 1.2.Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5 Ω and 9Ω as shown in the diagram below:
What is the potential difference across the terminals of the cell?
View SolutionA cell of emf 2 V and internal resistance 1.2Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5Ωand9Ω as shown in the diagram below:
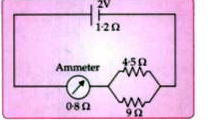
What is the potential difference across the terminals of the cell ?
View SolutionIn the situation shown , The potential difference across the cell of smaller e.m.f. is

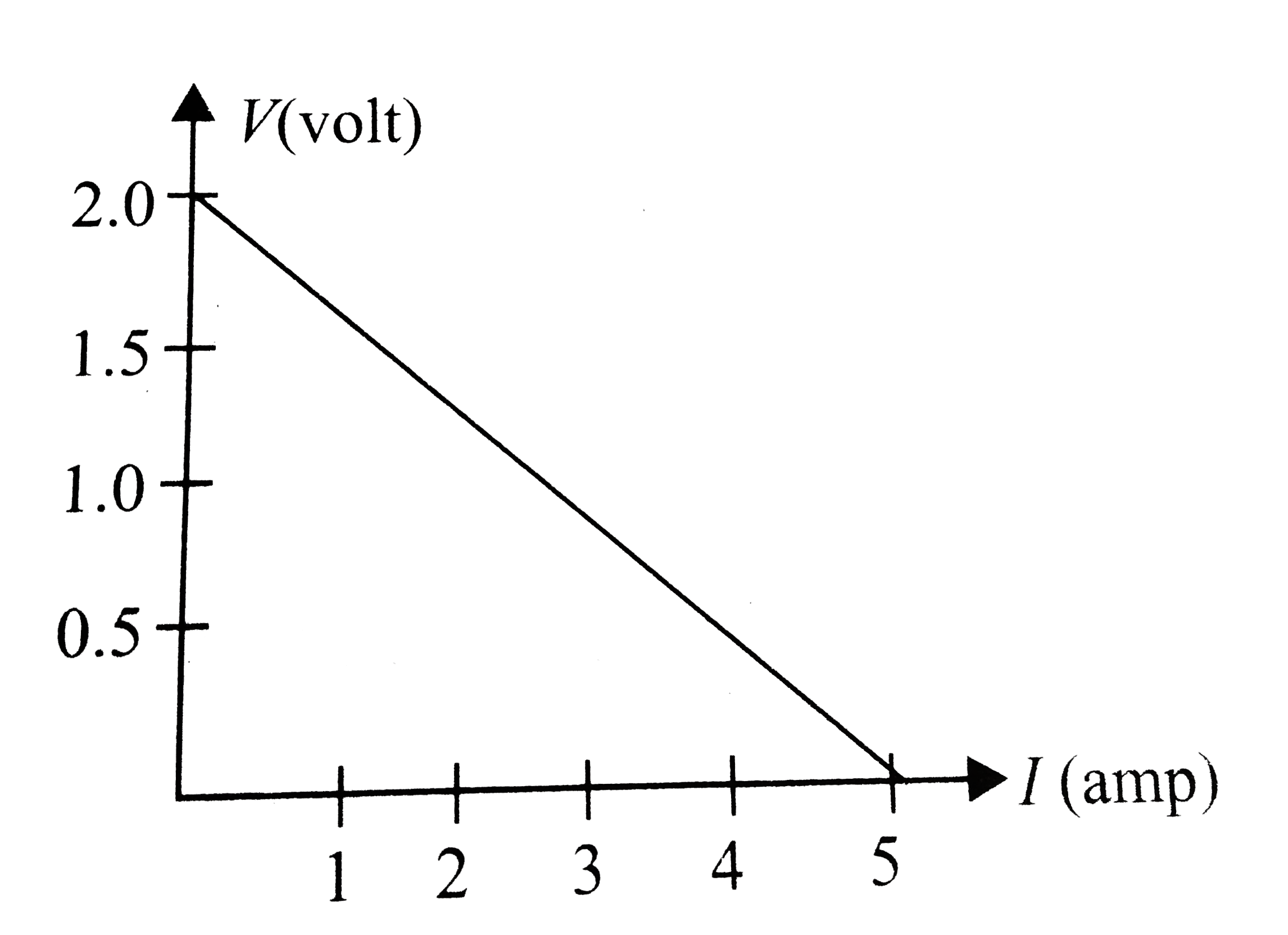
View SolutionFor the determination of emf E and internal resistance 'r' of a cell , the graph is obtained between potential difference V between the terminal of the cell against the current l, which was changed by adjusting the rheostat, is as shown . The internal resistance of the cell is
View Solution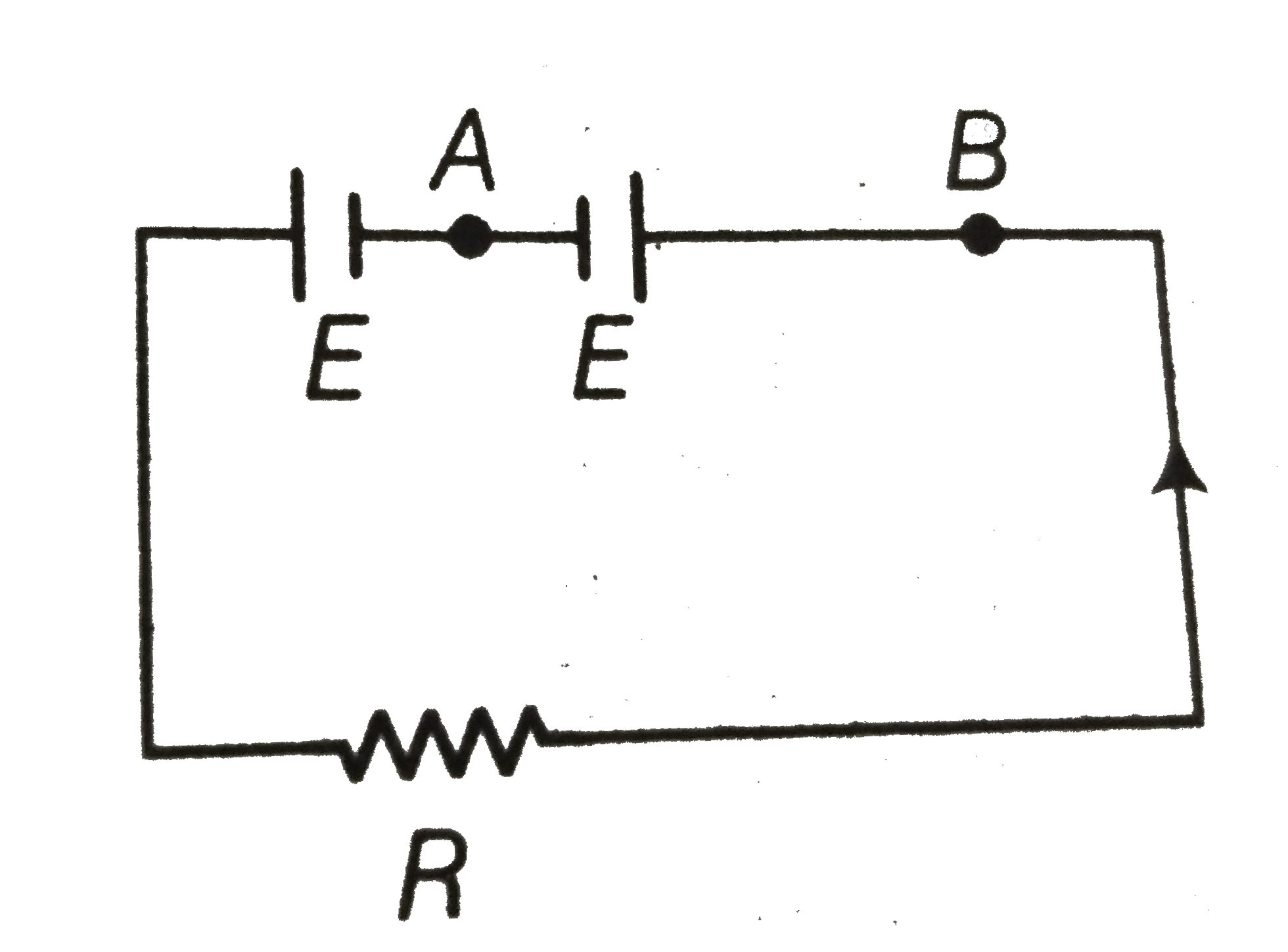
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
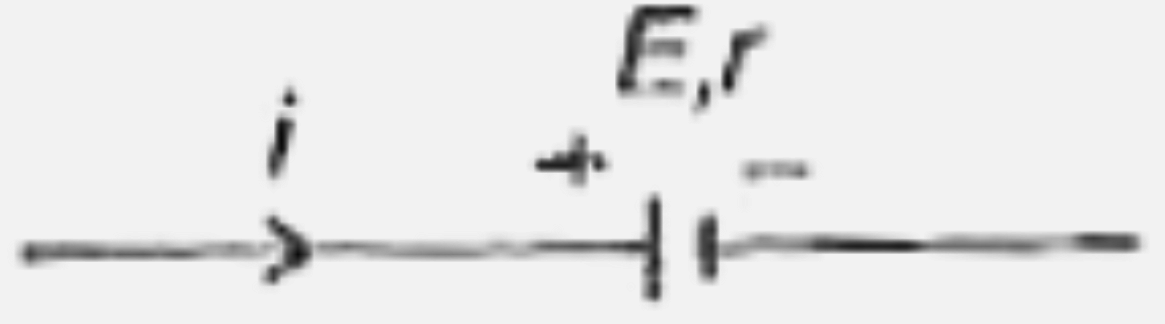
View Solution