A rod of length L and cross-section area A lies along the x-axis between x=0 and x=L. The material obeys Ohm's law and its resistivity varies along the rod according to ρ(x)=ρ0ε−x/L. The end of the rod x=0 is at a potential V0 and it is zero at x=L.
(a) Find the total resistance of the rod and the current in the wire.
(b) Find the electric potential in the rod as a function of x.
To solve the problem step by step, we will break it down into parts (a) and (b) as given in the question.
Part (a): Finding the Total Resistance of the Rod and the Current in the Wire
1. Understanding the Resistance of a Differential Element:
The resistivity of the rod varies with position x according to the formula:
ρ(x)=ρ0e−x/L
The resistance dR of a small element dx of the rod can be expressed as:
dR=ρ(x)dxA
Substituting for ρ(x):
dR=ρ0e−x/LdxA
2. Integrating to Find Total Resistance:
To find the total resistance R of the rod from x=0 to x=L, we integrate dR:
R=∫L0dR=∫L0ρ0e−x/LAdx
This integral can be solved as follows:
R=ρ0A∫L0e−x/Ldx
The integral of e−x/L is:
∫e−x/Ldx=−Le−x/L
Evaluating from 0 to L:
R=ρ0A(−Le−x/L)L0=ρ0A(−Le−1+L)=ρ0LA(1−1e)
3. Finding the Current:
The potential difference across the rod is V0 (at x=0) to 0 (at x=L). Using Ohm's law V=IR:
I=V0R=V0ρ0LA(1−1e)
Thus, the current I is:
I=V0A(1−1e)ρ0L
Part (b): Finding the Electric Potential in the Rod as a Function of x
1. Finding the Resistance from 0 to x:
The resistance Rx from x=0 to x is given by:
Rx=∫x0ρ0e−x′/LAdx′=ρ0A∫x0e−x′/Ldx′
Evaluating this integral:
Rx=ρ0A(−Le−x′/L)x0=ρ0LA(1−e−x/L)
2. Finding the Electric Potential V(x):
The potential at a distance x from the start of the rod can be expressed as:
V(x)=V0−IRx
Substituting I and Rx:
V(x)=V0−⎛⎜
⎜⎝V0A(1−1e)ρ0L⎞⎟
⎟⎠(ρ0LA(1−e−x/L))
Simplifying:
V(x)=V0−V0(1−1e)(1−e−x/L)
Thus:
V(x)=V0(e−x/L−1e)
Final Answers:
- Total Resistance:
R=ρ0LA(1−1e)
- Current:
I=V0A(1−1e)ρ0L
- Electric Potential:
V(x)=V0(e−x/L−1e)
The resistivity of the rod varies with position x according to the formula:
ρ(x)=ρ0e−x/L
The resistance dR of a small element dx of the rod can be expressed as:
dR=ρ(x)dxA
Substituting for ρ(x):
dR=ρ0e−x/LdxA
To find the total resistance R of the rod from x=0 to x=L, we integrate dR:
R=∫L0dR=∫L0ρ0e−x/LAdx
This integral can be solved as follows:
R=ρ0A∫L0e−x/Ldx
The integral of e−x/L is:
∫e−x/Ldx=−Le−x/L
Evaluating from 0 to L:
R=ρ0A(−Le−x/L)L0=ρ0A(−Le−1+L)=ρ0LA(1−1e)
The potential difference across the rod is V0 (at x=0) to 0 (at x=L). Using Ohm's law V=IR:
I=V0R=V0ρ0LA(1−1e)
Thus, the current I is:
I=V0A(1−1e)ρ0L
The resistance Rx from x=0 to x is given by:
Rx=∫x0ρ0e−x′/LAdx′=ρ0A∫x0e−x′/Ldx′
Evaluating this integral:
Rx=ρ0A(−Le−x′/L)x0=ρ0LA(1−e−x/L)
The potential at a distance x from the start of the rod can be expressed as:
V(x)=V0−IRx
Substituting I and Rx:
V(x)=V0−⎛⎜
⎜⎝V0A(1−1e)ρ0L⎞⎟
⎟⎠(ρ0LA(1−e−x/L))
Simplifying:
V(x)=V0−V0(1−1e)(1−e−x/L)
Thus:
V(x)=V0(e−x/L−1e)
- Total Resistance:
R=ρ0LA(1−1e)
- Current:
I=V0A(1−1e)ρ0L
- Electric Potential:
V(x)=V0(e−x/L−1e)
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-I(SUBJECTIVE TYPE QUESTIONS)14videos
CURRENT ELECTRICITY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)10videos
COMMUNICATION SYSTEMS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)10videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
A rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
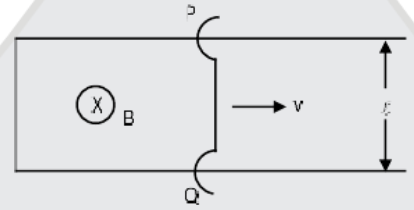 View Solution
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod isView SolutionA rod of length L is placed along the X-axis between x=0andx=L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. a.) Find the SI units of a and b b.) Find the mass of the rod in terms of a,b, and L.
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionA conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
View SolutionResistivity of a conductor of length l and cross - section A is ρ . If its length is doubled and area of cross-section is halved, then its new resistivity will be .
View SolutionAn insulting thin rod of length l has a linear charge density ρ(x)=ρ0xl on it. The rod is rotated about an axis passing through the origin (x=0) and perpendicular to the rod. If the rod makes n rotations per second, then the time averaged magnetic moment of the rod is :
View SolutionA rod resistor obeys non-linear relationship between V and l-according to I=√V/10 This rod is connected in series with a resistance to a 20 V battery of practically no resistance. Find this series resistance for the following cases
(a) the current in the circuit is 0.4 A.
(b) the power dissipated in the rod is twice that dissipated in the resistanceView SolutionA thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as kx4. Find the position of centre of mass of rod in meters.
View Solution

