A capacitor of capacitance C, which is initially uncharged , is connected with a battery of emf ε. Find the heat dissipated in the circuit during the process of charging .
Let R be the net resistance of the circuit.
During charging the charge on the capacitor varies as
q=q0(1−e−1/RC), wehre q0=εC
As i=dqdt⇒i=εR(e−1/RC)
Thermal power is given by dHdt=i2R⇒H=∫i2Rdt=ε2R2×R∫∞0e−2t/RCdt
gt H = ( epsilon^(2))/(R) [ (e^(-2 t //RC))/(2//RC)]_(0)^(infty)=(Cepsilon^(2))/(2) [-e^(-2t//RC)]_(0)^(infty) = (1)/(2) Cepsilon^(2) [ 1-0] = (1)/(2) C epsilon^(2)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
69 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
A capacitor of capacitance C which is initially charged up to a potential differnce ε is connected with a battery of emf ε2 such that the positive terminal of the battery is connected with the positive plate of the capacitor. Find the heat loss in the circuit the process of charging.
View SolutionA capacitor of capacitance C, which is initially charged up to a potential differnce ε, is connected with a battery of emf ε/2 such that the positive terminal of the battery is connected with the positive plate of the capacitor. After a long time.
i. find the total charge flow through the battery
ii. find the total work done by the battery
iii. Find the heat dissipated in the circuit during the process of charging.
View SolutionA capacitor of capacitance C carrying charge Q is connected to a source of emf E. Finally, the charge on capacitor would be
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance C is charged by connecting it to a battery of emf epsilon. The capacitor is now disconnected and reconnected to the battery with the polarity reversed. Calculate the heat developed in the connecting wires.
View SolutionA capacitor of capacitance C has charge Q. it is connected to an identical capacitor through a resistance. The heat produced in the resistance is
View SolutionThe capacitor C1 in the flgure shown initially carries a charge q0. When the switches S1 and S2 are closed,capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
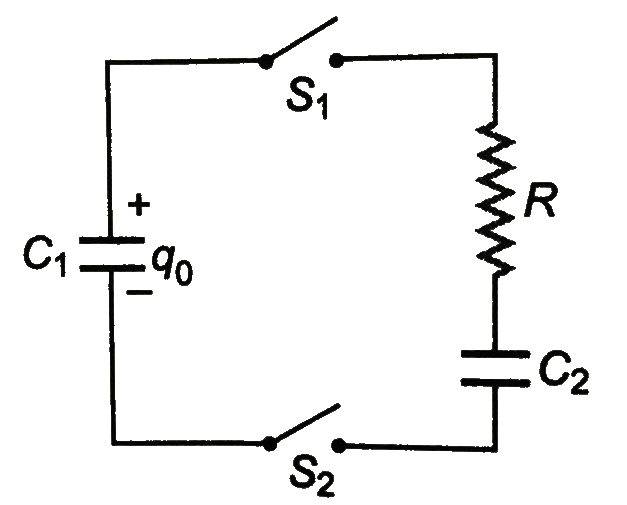
the total heat dissipated in the circuit during the discharging process of C1 is
View SolutionA 2μF capacitor that was initially uncharged is connected to a battery of EMF 100V and a resistance and the switch is closed. The heat generated in the resistance until the capacitor becomes fully charged is (in mJ):
View SolutionTwo parallel plate capacitors of capacitance C each are connected in series with a battery of emf ε. Then, one of the capacitors is filled with a dielectric of dielectric constane K.
i. Find the change in electric field in the two capacitors, if any
ii. What amount of charge flows through the battery?
iii Find the change in the energy stored in the circuit, if any.
View Solution
