A wire of length l and area A is connected to an ideal battery . The drift speed of electrons is v. If the wire is twisted to half its length, what will be the new drift speed ?
v
2v
v2
v4
The correct Answer is:B
To solve the problem step by step, we can follow these steps:
Step 1: Understand the relationship between current, drift velocity, and wire properties
The current I flowing through a wire can be expressed as:
I=n⋅A⋅e⋅vd
where:
- n = number of charge carriers per unit volume,
- A = cross-sectional area of the wire,
- e = charge of an electron,
- vd = drift velocity of the electrons.
Step 2: Relate current to resistance and voltage
From Ohm's law, we know that:
I=VR
where V is the voltage of the battery and R is the resistance of the wire. The resistance R of the wire can be expressed as:
R=ρLA
where:
- ρ = resistivity of the material,
- L = length of the wire.
Step 3: Substitute resistance into the current equation
Substituting the expression for resistance into the current equation gives us:
I=VρLA=V⋅AρL
Step 4: Set the two expressions for current equal to each other
Now we can set the two expressions for current equal to each other:
n⋅A⋅e⋅vd=V⋅AρL
Here, we can cancel A from both sides:
n⋅e⋅vd=VρL
Step 5: Express the relationship between drift velocity and length
From the above equation, we can express vd:
vd=VρneL
This shows that drift velocity vd is inversely proportional to the length L of the wire.
Step 6: Analyze the change in length of the wire
If the wire is twisted to half its length, the new length L2 becomes:
L2=L2
Step 7: Relate the new drift velocity to the original drift velocity
Using the relationship derived earlier, we can write:
vd2=VρneL2
Substituting L2=L2:
vd2=Vρne(L2)=2VρneL
Step 8: Compare the new drift velocity with the original drift velocity
Since the original drift velocity vd=VρneL, we can relate the new drift velocity to the original:
vd2=2⋅vd
Final Result
Thus, the new drift speed vd2 when the wire is twisted to half its length is:
vd2=2v
The current I flowing through a wire can be expressed as:
I=n⋅A⋅e⋅vd
where:
- n = number of charge carriers per unit volume,
- A = cross-sectional area of the wire,
- e = charge of an electron,
- vd = drift velocity of the electrons.
From Ohm's law, we know that:
I=VR
where V is the voltage of the battery and R is the resistance of the wire. The resistance R of the wire can be expressed as:
R=ρLA
where:
- ρ = resistivity of the material,
- L = length of the wire.
Substituting the expression for resistance into the current equation gives us:
I=VρLA=V⋅AρL
Now we can set the two expressions for current equal to each other:
n⋅A⋅e⋅vd=V⋅AρL
Here, we can cancel A from both sides:
n⋅e⋅vd=VρL
From the above equation, we can express vd:
vd=VρneL
This shows that drift velocity vd is inversely proportional to the length L of the wire.
If the wire is twisted to half its length, the new length L2 becomes:
L2=L2
Using the relationship derived earlier, we can write:
vd2=VρneL2
Substituting L2=L2:
vd2=Vρne(L2)=2VρneL
Since the original drift velocity vd=VρneL, we can relate the new drift velocity to the original:
vd2=2⋅vd
Thus, the new drift speed vd2 when the wire is twisted to half its length is:
vd2=2v
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
13 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
69 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2LA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl
A wire of resistivity is stretched to double its length. What will be its new resistivity?
View SolutionIf a wire of resistance R is melted and recasted in to half of its length, then the new resistance of the wire will be
View SolutionIn a wire of length L, the increase in its length is l. If the length is reduced to half, the increase in its length will be
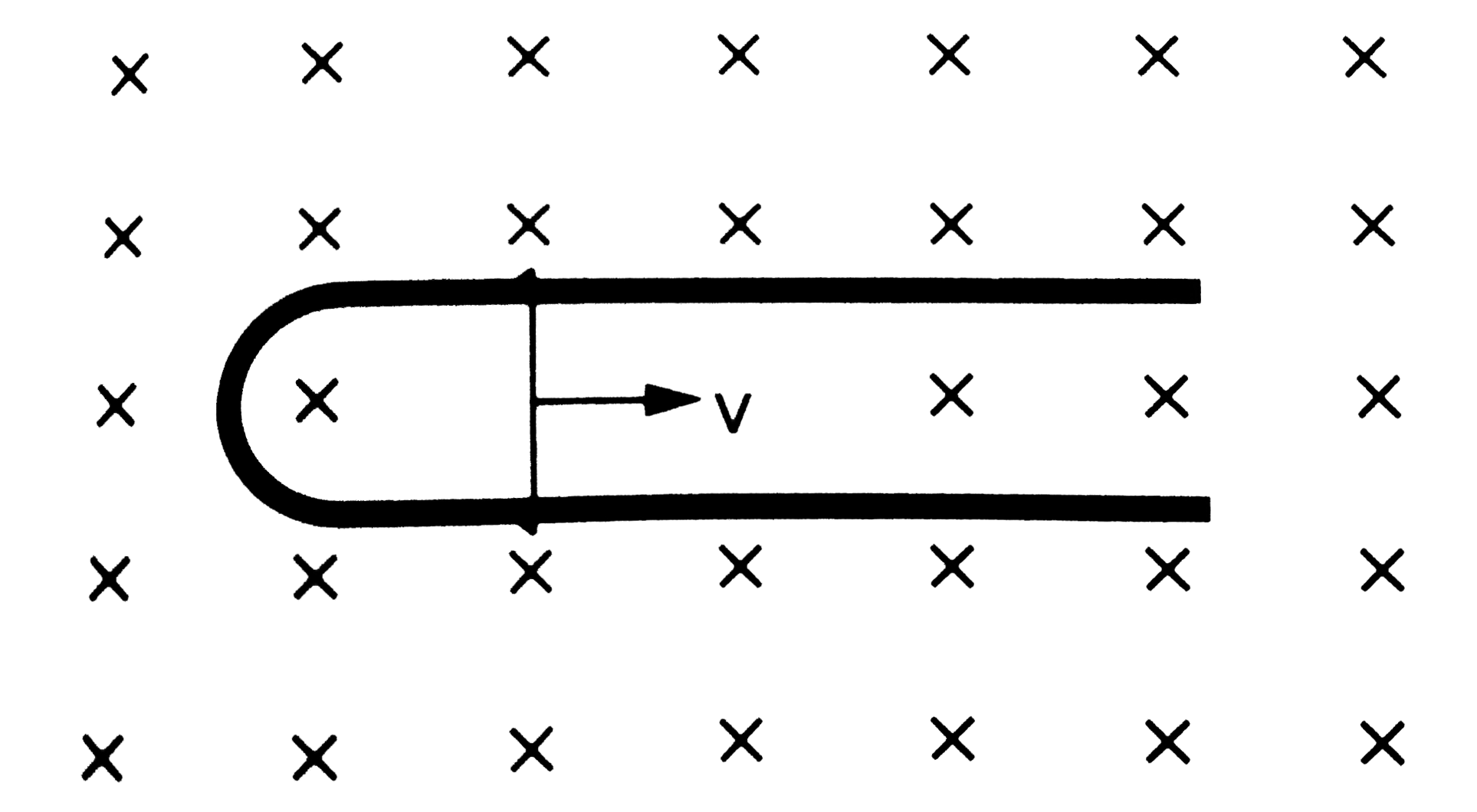
View SolutionShows a wire of length l which can slide on a U- shaped rail of negligible resistance. The resistance of the wire is R. The wire is pulled ot the right with a constant speed v. Draw an equivalent circuit diagram representing the induced emf by a battery. Find the current in the wire usingj this diagram.

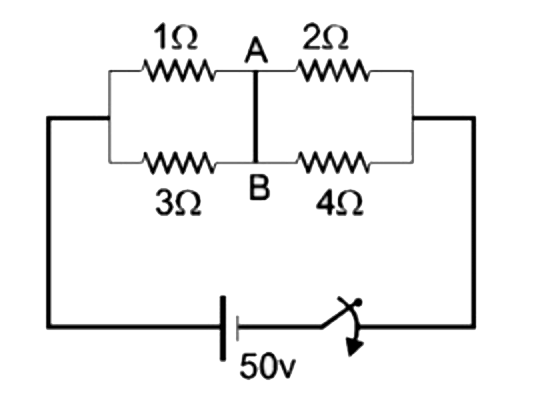
View SolutionFor resistances are connected by an ideal battery of emf 15 V, the circuit is in steady - state then the current (in ampere) in wire AB is :
View SolutionA steel wire of length l and cross sectional area A is stretched by 1 cm under a given load. When the same load is applied to another steel wire of double its length and half of its cross section area, the amount of stretching (extension) is
View Solution
