STATEMENT-1 : In the absence of current in a counducting wire, the random motionof electrons is zig-zag with electrons moving in a straight line between two successive collisions.
and
STATEMENT-2 : When a c urrent is set up, the path of electrons between two successive collisions becomes curved.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False , Statement-2 is True
The correct Answer is:2
To solve the problem, we need to analyze both statements provided in the question and determine their validity based on our understanding of the behavior of electrons in a conducting wire under different conditions.
Step 1: Analyze Statement 1
Statement 1 claims that in the absence of current in a conducting wire, the random motion of electrons is zig-zag, with electrons moving in a straight line between two successive collisions.
- Explanation: In a conductor without an applied electric field (no current), the electrons are indeed in random motion due to thermal energy. This random motion can be described as zig-zag because the electrons are constantly colliding with the lattice ions of the conductor. However, between these collisions, they travel in straight lines. Hence, this statement is true.
Step 2: Analyze Statement 2
Statement 2 claims that when a current is set up, the path of electrons between two successive collisions becomes curved.
- Explanation: When an electric field is applied to the conductor, the electrons experience a force in the opposite direction of the electric field, causing them to drift in that direction. While they still move in straight lines between collisions, their overall motion is influenced by the electric field, resulting in a net movement in the direction opposite to the electric field. Therefore, the path of electrons between collisions remains straight, and this statement is false.
Conclusion:
- Statement 1 is true.
- Statement 2 is false.
Thus, the correct answer is that Statement 1 is true, and Statement 2 is false.
Statement 1 claims that in the absence of current in a conducting wire, the random motion of electrons is zig-zag, with electrons moving in a straight line between two successive collisions.
Statement 2 claims that when a current is set up, the path of electrons between two successive collisions becomes curved.
- Statement 1 is true.
- Statement 2 is false.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-J(MATRIX-MATCH TYPE QUESTIONS)
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-H( INTEGER ANSWER TYPE QUESTIONS)
5 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS) Comprehension - II
5 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Are the paths of free electrons straight lines between successive collisions (with the positive ions of metal wire) in the-
(i) Absence of electric field (ii) Presence of electric field
View SolutionA particle performs SHM on a straight line with time period T and amplitudeA. The average speed of the particle between two successive instants, when potential energy and kinetic energy become same is
View SolutionSTATEMENT-1 : In an elastic collision between two balls, the total kinetic energy of the two bodies does not remain conserved during the collision.
and
STATEMENT-2 : As the balls collide, they compress each other.
View SolutionEstimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2 atm and temperature 17∘C. Take the radius of a nitrogen molecule to be roughly 1.0Å. Compare the collision time with the time the molecule moves freely between two successive collisions. (Molecular mass of nitrogen = 28.0 u).
View SolutionEstimate the mean free path and collison frequency of a nitrogen molecule in a cylinder containing nitrogen at 2.0 atm and temperature 17∘C. Take the radius of a nitrogen molecule to be roughtly 1.0 Å . Compare the collision time with the time the molecule moves freely between two successive collision ( molecular mass of N2=28.0 ) . [Optional ]
View SolutionSTATEMENT-1 : In the decay of a free neutron at rest, into a proton and electron, it has been predicated that a third particle must also be emitted because the emitted electrons do not have a definite kinetic energy.
and
STATEMENT-2 : For the simple decay of a stationary particle into two moving particles, the kinetic energies of the particle must have a sharply defined value.
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
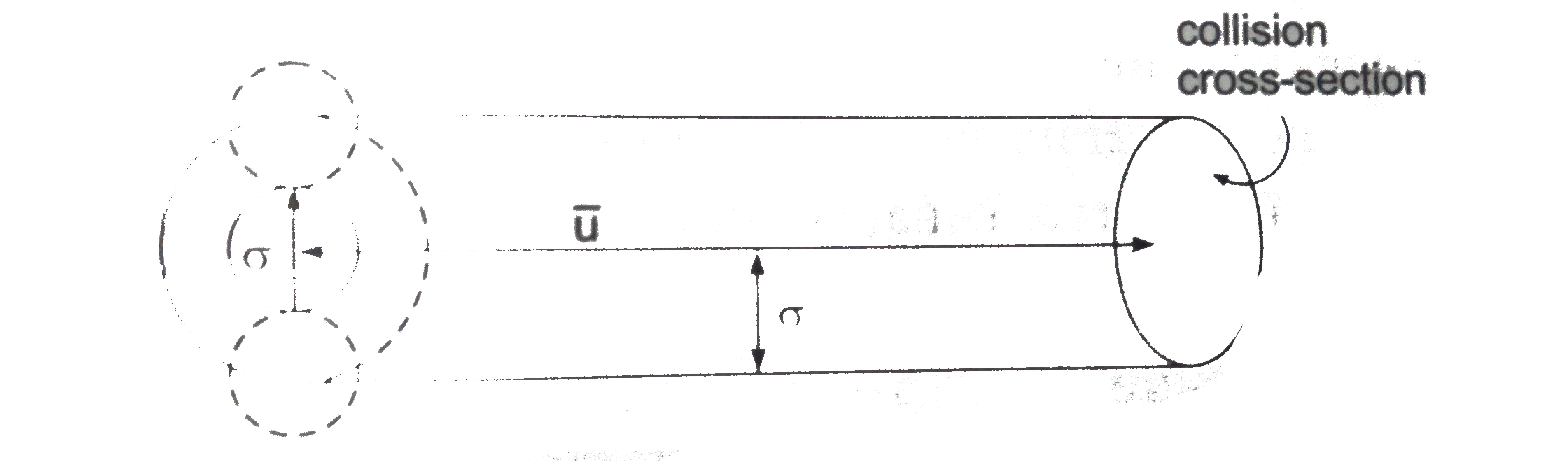
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
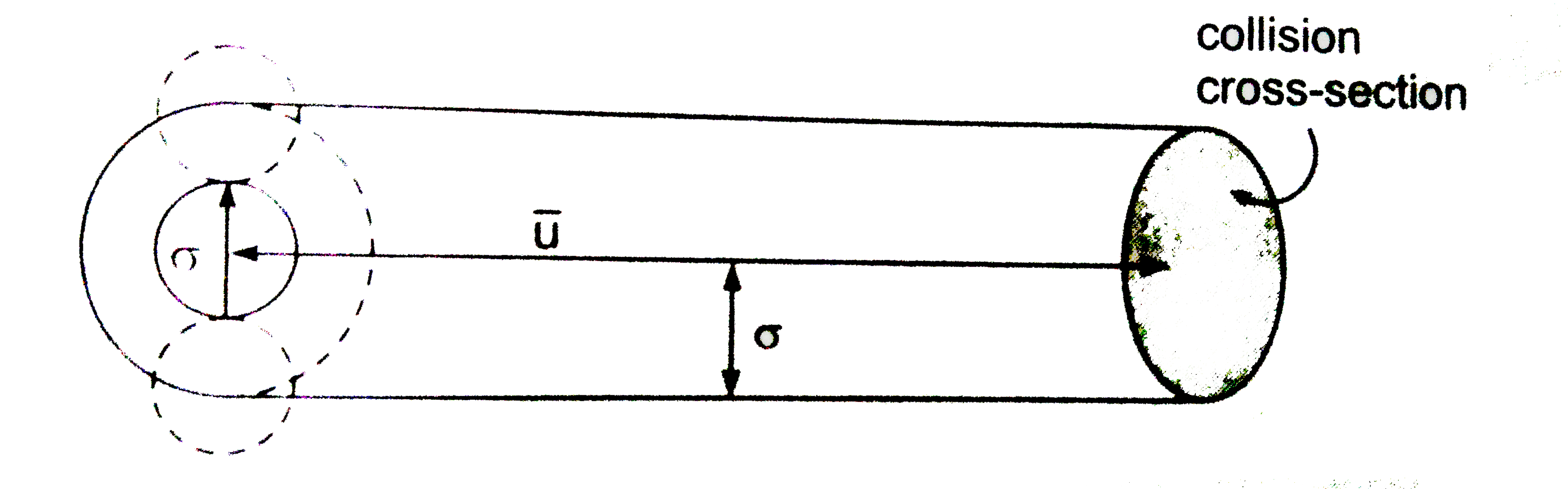
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate ratio of collision frequencies (Z11)(A:B:C) of following for the three gases.
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A current of 1 A flows through a copper wire. The number of electrons passing through any cross-section of the wire in 1.6 sec is (charge of a electron = 1.6 xx 10^(-19 c).
View SolutionThe root mean square speed of an ideal gas is given by : urms=√3RTM Thus we conclude that urms speed of the ideal gas molecules is proportional to square root of the temperature and inversely proportional to the square root of the molar mass. The translational kinetic energy per mole can also be given as 12Mu2rms . The mean free path (λ) is the average of distances travelled by molecules in between two successive collisions whereas collision frequency (C.F.) is expressed as number of collisions taking place in unit time. The two terms λ and C.F. are related by : C.F=(urmsλ)
A jar contains He and H, in the molar ratio 1 : 5. The ratio of mean translational kinetic energy at the same temperature is
View Solution
