Two cells of same emf but different internal resistance are connected in parallel so as to send current in same direction.
STATEMENT-1 : The equivalent emf of the combination is equal to individual emf of each cell.
and
STATEMENT-2 : The equivalent emf is the arithmetic mean of the individual emfs.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1
Statement-1 is True, Statement-2 is True
Statement-1 is False , Statement-2 is True
The correct Answer is:3
To solve the problem, we need to analyze the statements regarding the equivalent EMF of two cells connected in parallel with different internal resistances.
1. Understanding the Configuration:
- We have two cells, each with the same EMF (let's call it E) but different internal resistances (let's denote them as R1 and R2).
- These cells are connected in parallel in such a way that they send current in the same direction.
2. Applying Kirchhoff's Law:
- When connected in parallel, the voltage across both cells must be the same. Let this common voltage be V.
- For cell 1: The current I1 flowing through it can be expressed as:
I1=V−ER1
- For cell 2: The current I2 flowing through it can be expressed as:
I2=V−ER2
3. Total Current in the Circuit:
- The total current I flowing from the combination of the two cells is the sum of the individual currents:
I=I1+I2=V−ER1+V−ER2
4. Rearranging the Equation:
- We can factor out (V - E):
I=(V−E)(1R1+1R2)
5. Finding the Equivalent EMF:
- We can express the equivalent EMF (E_eq) in terms of the currents and resistances:
Eeq=ER1+ER2÷(1R1+1R2)
- This shows that the equivalent EMF is not simply equal to the individual EMF E.
6. Evaluating the Statements:
- Statement 1: "The equivalent EMF of the combination is equal to individual EMF of each cell."
- This statement is True because the voltage across the parallel combination remains equal to the EMF of the cells.
- Statement 2: "The equivalent EMF is the arithmetic mean of the individual EMFs."
- This statement is False because the equivalent EMF is not the arithmetic mean but rather a weighted average based on the internal resistances.
Conclusion:
- Final Answer: Statement 1 is true, and Statement 2 is false.
- We have two cells, each with the same EMF (let's call it E) but different internal resistances (let's denote them as R1 and R2).
- These cells are connected in parallel in such a way that they send current in the same direction.
- When connected in parallel, the voltage across both cells must be the same. Let this common voltage be V.
- For cell 1: The current I1 flowing through it can be expressed as:
I1=V−ER1
- For cell 2: The current I2 flowing through it can be expressed as:
I2=V−ER2
- The total current I flowing from the combination of the two cells is the sum of the individual currents:
I=I1+I2=V−ER1+V−ER2
- We can factor out (V - E):
I=(V−E)(1R1+1R2)
- We can express the equivalent EMF (E_eq) in terms of the currents and resistances:
Eeq=ER1+ER2÷(1R1+1R2)
- This shows that the equivalent EMF is not simply equal to the individual EMF E.
- Statement 1: "The equivalent EMF of the combination is equal to individual EMF of each cell."
- This statement is True because the voltage across the parallel combination remains equal to the EMF of the cells.
- Statement 2: "The equivalent EMF is the arithmetic mean of the individual EMFs."
- This statement is False because the equivalent EMF is not the arithmetic mean but rather a weighted average based on the internal resistances.
- Final Answer: Statement 1 is true, and Statement 2 is false.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-J(MATRIX-MATCH TYPE QUESTIONS)
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-H( INTEGER ANSWER TYPE QUESTIONS)
5 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS) Comprehension - II
5 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Two batteries of different emfs and different internal resistances are connected as shown. The voltage across AB in volts is.
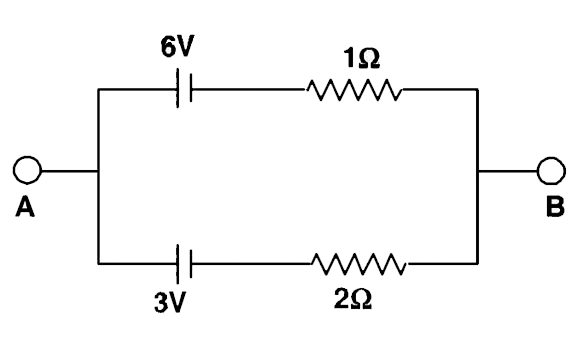 .
.
View SolutionFive cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
View Solution
Knowledge Check
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
Two cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThousand cells of same emf E and same internal resistance r are connected is series in same order without an external resistance . The potential drop across 399 cells is found to be .
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
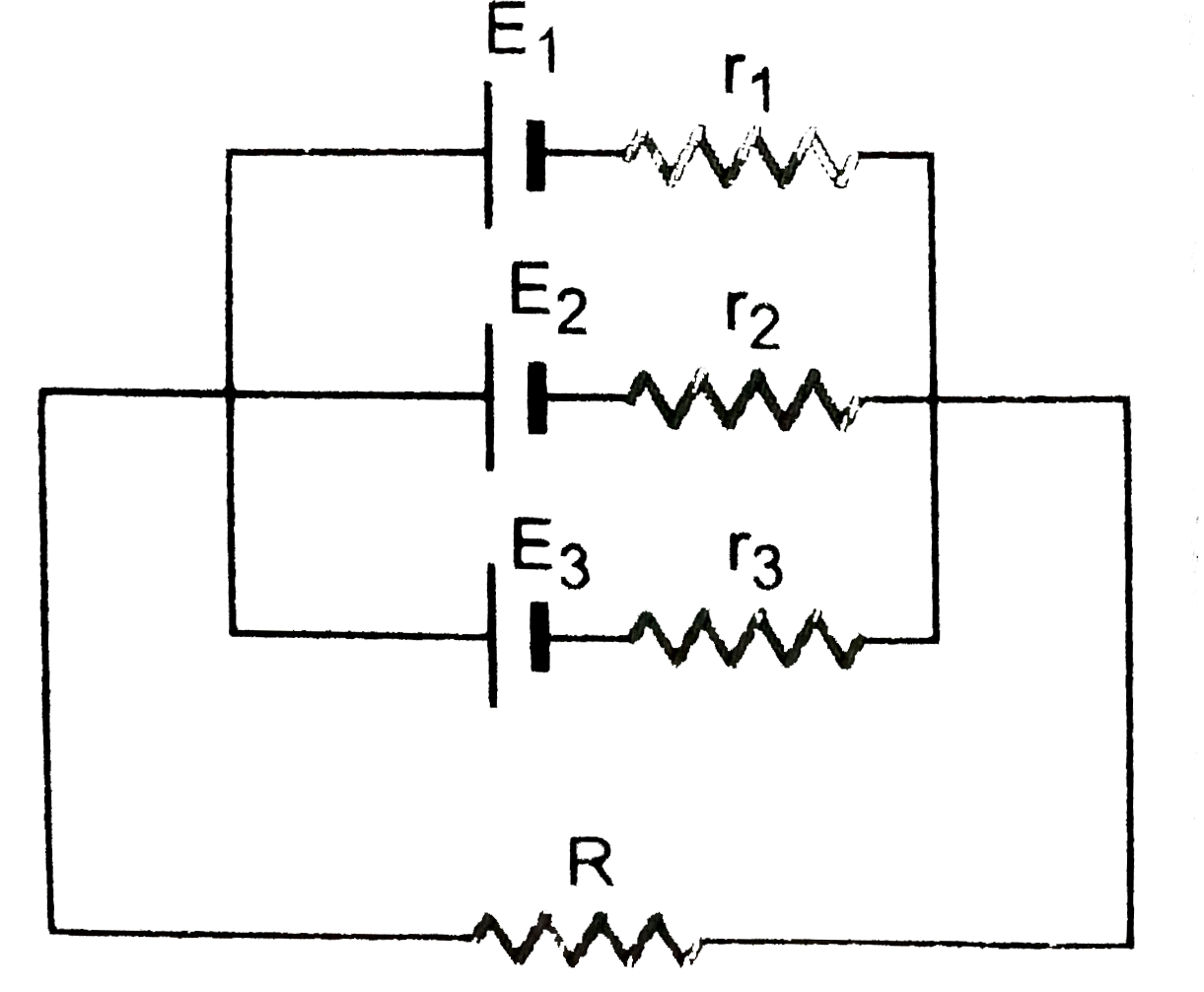
View SolutionA : When two cells of equal EMF and equal internal resistances are connected is parallel with positive plate of the other than , the net EMF , of the combination will be equal to the EMF of each cell.
R : Effective internal resistance of the parallel combination of two identical cells will be half of the internal resistance of each cell.
View Solution
