A rod resistor obeys non-linear relationship between V and l-according to I=√V/10 This rod is connected in series with a resistance to a 20 V battery of practically no resistance. Find this series resistance for the following cases
(a) the current in the circuit is 0.4 A.
(b) the power dissipated in the rod is twice that dissipated in the resistance
To solve the problem, we need to analyze the given information step by step.
Given:
1. The relationship between current (I) and voltage (V) for the rod resistor is given by:
I=√V10
2. The rod is connected in series with a resistance Rs to a 20 V battery.
Part (a): Find the series resistance when the current in the circuit is 0.4 A.
Step 1: Find the voltage across the rod resistor when the current is 0.4 A.
Using the relationship I=√V10:
0.4=√V10
Squaring both sides:
(0.4)2=V10
0.16=V10
Multiplying both sides by 10:
V=1.6 V
Step 2: Find the voltage across the series resistance Rs.
The total voltage supplied by the battery is 20 V. Therefore, the voltage across the series resistance Rs is:
VRs=Vbattery−Vrod=20 V−1.6 V=18.4 V
Step 3: Use Ohm's Law to find the series resistance Rs.
Using Ohm's Law V=I⋅R:
VRs=I⋅Rs
Substituting the known values:
18.4=0.4⋅Rs
Solving for Rs:
Rs=18.40.4=46Ω
Part (b): Find the series resistance when the power dissipated in the rod is twice that dissipated in the resistance.
Step 1: Find the power dissipated in the rod resistor.
The power P dissipated in the rod resistor can be calculated using:
Prod=I2⋅Rrod
Where Rrod can be calculated using Vrod and I:
Rrod=VrodI=1.60.4=4Ω
Thus, the power in the rod is:
Prod=(0.4)2⋅4=0.16⋅4=0.64 W
Step 2: Find the power dissipated in the series resistance Rs.
According to the problem, the power in the rod is twice that in the series resistance:
Prod=2⋅PRs
Thus:
0.64=2⋅PRs⟹PRs=0.642=0.32 W
Step 3: Find the current through the circuit using the power formula.
Using the power formula for the series resistance:
PRs=I2⋅Rs
Substituting the known values:
0.32=(0.4)2⋅Rs
Solving for Rs:
0.32=0.16⋅Rs⟹Rs=0.320.16=2Ω
Final Answers:
(a) The series resistance Rs=46Ω.
(b) The series resistance Rs=2Ω.
1. The relationship between current (I) and voltage (V) for the rod resistor is given by:
I=√V10
2. The rod is connected in series with a resistance Rs to a 20 V battery.
Using the relationship I=√V10:
0.4=√V10
Squaring both sides:
(0.4)2=V10
0.16=V10
Multiplying both sides by 10:
V=1.6 V
The total voltage supplied by the battery is 20 V. Therefore, the voltage across the series resistance Rs is:
VRs=Vbattery−Vrod=20 V−1.6 V=18.4 V
Using Ohm's Law V=I⋅R:
VRs=I⋅Rs
Substituting the known values:
18.4=0.4⋅Rs
Solving for Rs:
Rs=18.40.4=46Ω
The power P dissipated in the rod resistor can be calculated using:
Prod=I2⋅Rrod
Where Rrod can be calculated using Vrod and I:
Rrod=VrodI=1.60.4=4Ω
Thus, the power in the rod is:
Prod=(0.4)2⋅4=0.16⋅4=0.64 W
According to the problem, the power in the rod is twice that in the series resistance:
Prod=2⋅PRs
Thus:
0.64=2⋅PRs⟹PRs=0.642=0.32 W
Using the power formula for the series resistance:
PRs=I2⋅Rs
Substituting the known values:
0.32=(0.4)2⋅Rs
Solving for Rs:
0.32=0.16⋅Rs⟹Rs=0.320.16=2Ω
(a) The series resistance Rs=46Ω.
(b) The series resistance Rs=2Ω.
Similar Questions
The current I through a rod of a certain metallic oxide is given by I=0.2V1/2 , where V is the potential difference cross it. The rod is connected in series with a resistance to a 6 volt battery of negligible internal resistance. What value should the series resistance have so that :
A) the current in the circuit is 0.4 A
B) the power dissipated in the rod is twice that dissipated in the resistance.View Solution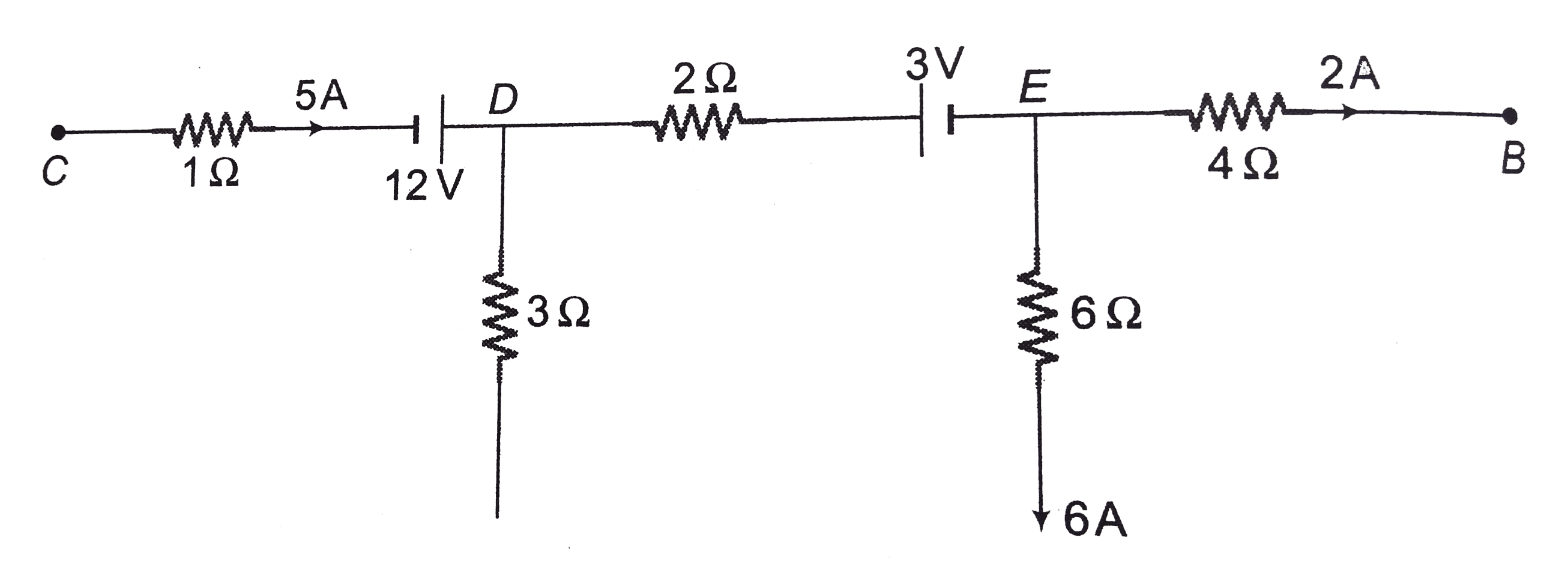 Figure shows the part of a circuit. Calculate the power dissipated in 3ohm resistance. What is the potential difference VC−VB?View Solution
Figure shows the part of a circuit. Calculate the power dissipated in 3ohm resistance. What is the potential difference VC−VB?View SolutionA resistor and a capacitor are connected to an ac supply of 200 V, 50 Hz, in series. The current in the circuit is 2A. If the power consumed in the circuit is 100 W then the resistance in the circuit is
View SolutionA resistor and a capacitor are connected to an ac supply of 200 V, 50 Hz, in series. The current in the circuit is 2A. If the power consumed in the circuit is 100 W then the resistance in the circuit is
View SolutionTwo cells having emf's of 10 V and 8 V, respectively, are connected in series with a resistance of 24Ω In the external circuit. Their internal resistances are 2Ω/V (proportional to their emf's). Find the current in the circuit
 View Solution
View SolutionAssume that the batteries in figure have negligible internal resistance. Find
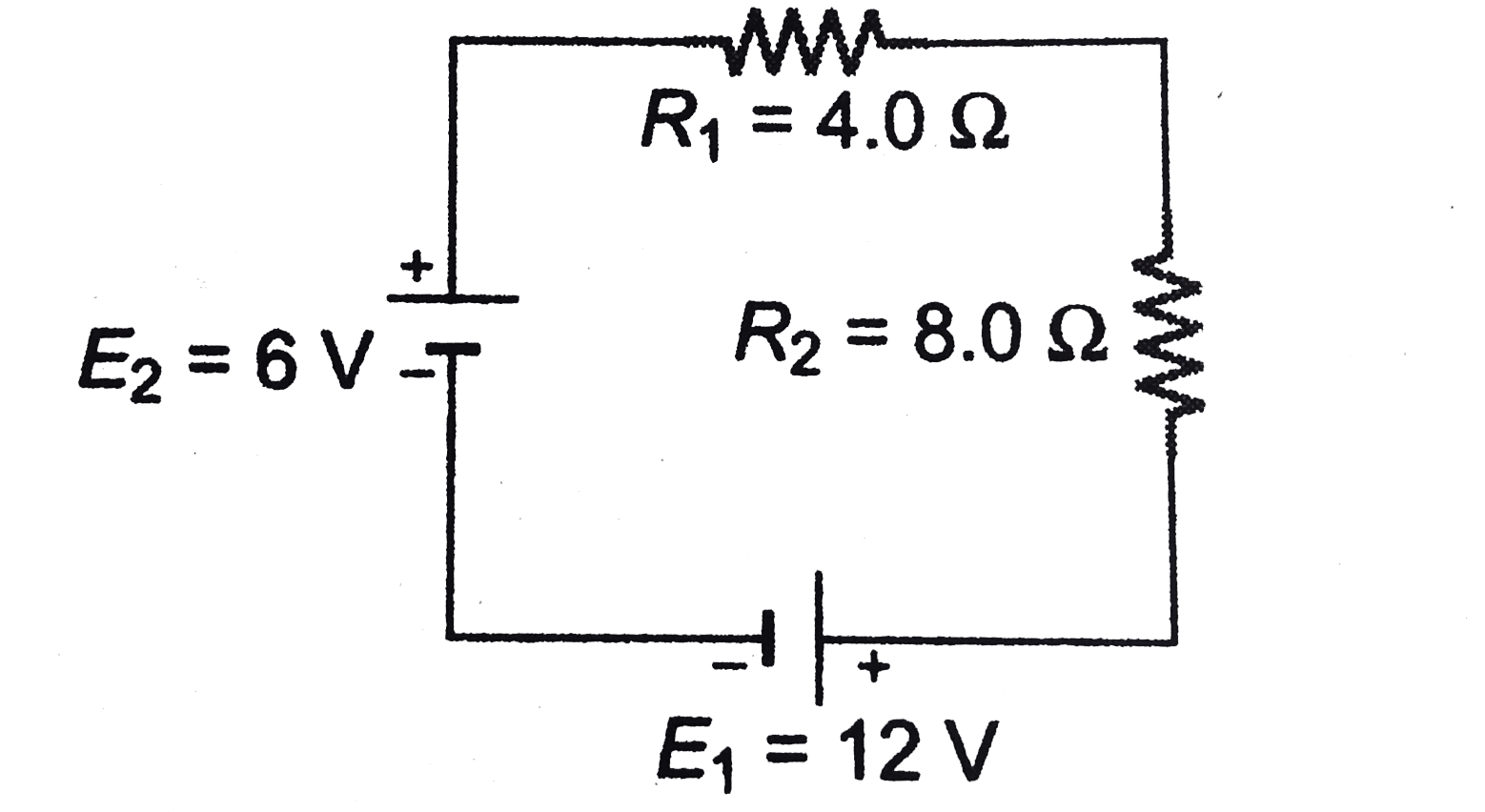
a. the current in the circuit,
(b) the power dissipated in each resistor and
(c) the power of each battery, stating whether energy is supplied by or absorbed by itView SolutionA battery of 3.0 V is connected to a resistor dissipating 0.5 W of power . If the terminal voltage of the battery is 2.5 V , the power dissipated within the internal resistance is :
View SolutionA battery of emf 12V and internal resistance 2Ω is connected with two resistors A and B of resistance 4Ω and 6Ω respectively joined in series. . The current i in the circuit is
View SolutionA 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Ω as shown in figure.
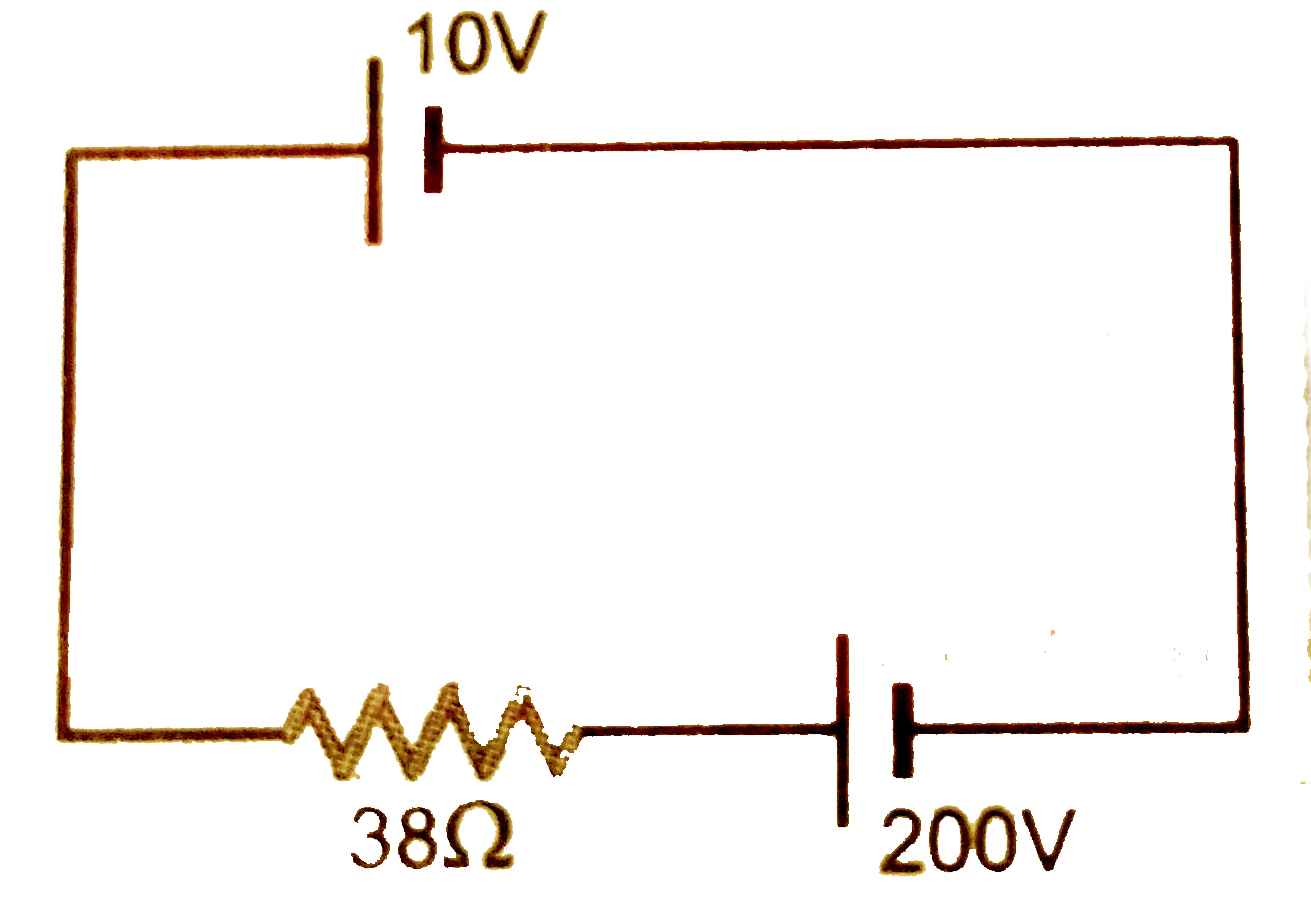 . Find the value of current in the circuit.View Solution
. Find the value of current in the circuit.View SolutionA capacitor of capacitance 10μF is connected to a resistance 2Ω and a battery of emf 5V of negligible interanl resistance. After 20μs of comleting the circuit find.
a. power delivered by the battery
b. power dissipated as heat
c. rate of energy stored in the capacitorView Solution

