A ball of mass m is thrown upward and another ball of same mass is thrown downward so as to move freely gravity. The acceleration of centre of mass is
g
2g
Zero
The correct Answer is:A
To find the acceleration of the center of mass of the two balls, we can follow these steps:
1. Identify the masses and their accelerations:
- Let the mass of each ball be m.
- The first ball is thrown upward, and its acceleration due to gravity is −g (downward).
- The second ball is thrown downward, and its acceleration is also −g (downward).
2. Write down the formula for the acceleration of the center of mass:
- The acceleration of the center of mass acm for a system of particles is given by:
acm=m1a1+m2a2m1+m2
- Here, m1=m, a1=−g (for the ball thrown upward), m2=m, and a2=−g (for the ball thrown downward).
3. Substitute the values into the formula:
- Substitute m1, a1, m2, and a2 into the formula:
acm=m(−g)+m(−g)m+m
4. Simplify the equation:
- Combine the terms in the numerator:
acm=−mg−mg2m=−2mg2m
- This simplifies to:
acm=−g
5. Interpret the result:
- The negative sign indicates that the acceleration of the center of mass is directed downward, which means the acceleration of the center of mass is g downward.
Final Answer:
The acceleration of the center of mass is g downward.
---
- Let the mass of each ball be m.
- The first ball is thrown upward, and its acceleration due to gravity is −g (downward).
- The second ball is thrown downward, and its acceleration is also −g (downward).
- The acceleration of the center of mass acm for a system of particles is given by:
acm=m1a1+m2a2m1+m2
- Here, m1=m, a1=−g (for the ball thrown upward), m2=m, and a2=−g (for the ball thrown downward).
- Substitute m1, a1, m2, and a2 into the formula:
acm=m(−g)+m(−g)m+m
- Combine the terms in the numerator:
acm=−mg−mg2m=−2mg2m
- This simplifies to:
acm=−g
- The negative sign indicates that the acceleration of the center of mass is directed downward, which means the acceleration of the center of mass is g downward.
The acceleration of the center of mass is g downward.
Similar Questions
A particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View Solution
Knowledge Check
A ball of mass M is thrown vertically upwards. Another ball of mass 2M is thrown at an angle θ with the vertical. Both of them stay in air for the same period of time. The heights attained by the two are in the ratio
A1:2B2:1C1:1D1:cosθ
If a ball is thrown upwards from the surface of earth :
View SolutionA ball of mass (m) is thrown vertically up. Another ball of mass 2m is thrown at an angle θ with the vertical. Both of them stay in air for the same period of time. What is the ratio of the height attained by two balls.
View SolutionTwo balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
View SolutionA ball of mass 2kg is thrown with velocity 10ms at an angle of 30°to the horizontal and another ball with the same mass is thrown at an angel of 60° to the horizontal with the same speed.The ratio will be their range will be
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
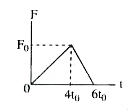
Average force exerted by the bat on the ball is
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
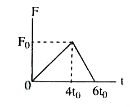
Maximum force exerted by the bat on the ball is
View SolutionA ball of mass 'm' is thrown vertically up-ward from the ground and reached a height 'h' before momentarily coming to rest , If 'g' is acceleration due to gravity . What is the impulse received by the ball due to gravity force during its flight ? (neglect air resistance )
View Solution
