A wheel starts from rest and attains an angular velocity of 20 radian/s after being uniformly accelerated for 10 s. The total angle in radian through which it has turned in 10 second is
20π
40π
100
100π
The correct Answer is:C
To solve the problem step by step, we'll use the equations of rotational motion.
Step 1: Identify the given values
- Initial angular velocity (ωi) = 0 rad/s (since the wheel starts from rest)
- Final angular velocity (ωf) = 20 rad/s
- Time (t) = 10 s
Step 2: Calculate the angular acceleration (α)
We can use the formula relating final angular velocity, initial angular velocity, angular acceleration, and time:
ωf=ωi+αt
Substituting the known values:
20=0+α⋅10
This simplifies to:
α=2010=2 rad/s2
Step 3: Calculate the total angle (θ) turned in 10 seconds
We can use the equation for angular displacement:
θ=ωit+12αt2
Substituting the known values:
θ=0⋅10+12⋅2⋅(10)2
This simplifies to:
θ=0+12⋅2⋅100=100 radians
Final Answer
The total angle through which the wheel has turned in 10 seconds is 100 radians.
---
- Initial angular velocity (ωi) = 0 rad/s (since the wheel starts from rest)
- Final angular velocity (ωf) = 20 rad/s
- Time (t) = 10 s
We can use the formula relating final angular velocity, initial angular velocity, angular acceleration, and time:
ωf=ωi+αt
Substituting the known values:
20=0+α⋅10
This simplifies to:
α=2010=2 rad/s2
We can use the equation for angular displacement:
θ=ωit+12αt2
Substituting the known values:
θ=0⋅10+12⋅2⋅(10)2
This simplifies to:
θ=0+12⋅2⋅100=100 radians
The total angle through which the wheel has turned in 10 seconds is 100 radians.
Similar Questions
A flywheel at rest is to reach an angular velocity of 24 rad/s in 8 second with constant angular acceleration. The total angle turned through during this interval is
View SolutionA wheel is a rest. Its angular velocity increases uniformly and becomes 80rads−1 after 5 s. The total angular displacement is
View Solution
Knowledge Check
A wheel make 450 revolutions per hour. The number of radians through which its turn in one second is
Aπ4Bπ2Cπ6Dπ3
A wheel starts rotating at 10 rad/sec and attains the angular velocity of 100 rad/sec in 15 seconds. What is the angular acceleration in rad/sec2?
View SolutionA wheel is at rest. Its angular velocity increases uniformly and becomes 80 radian per second after 5 second. The total angular displacement is :-
View SolutionIf a disc starting from rest acquires an angular velocity of 240rev min−1 in 10 s, then its angular acceleration will be
View SolutionA wheel starts rotating with an-angular velocity of 2 rad/s. If it rotates with a constant angular acceleration 4rad/s2 what angle does the wheel rotate through in 2.0 s ? What is the angular speed, after 2.0 s.
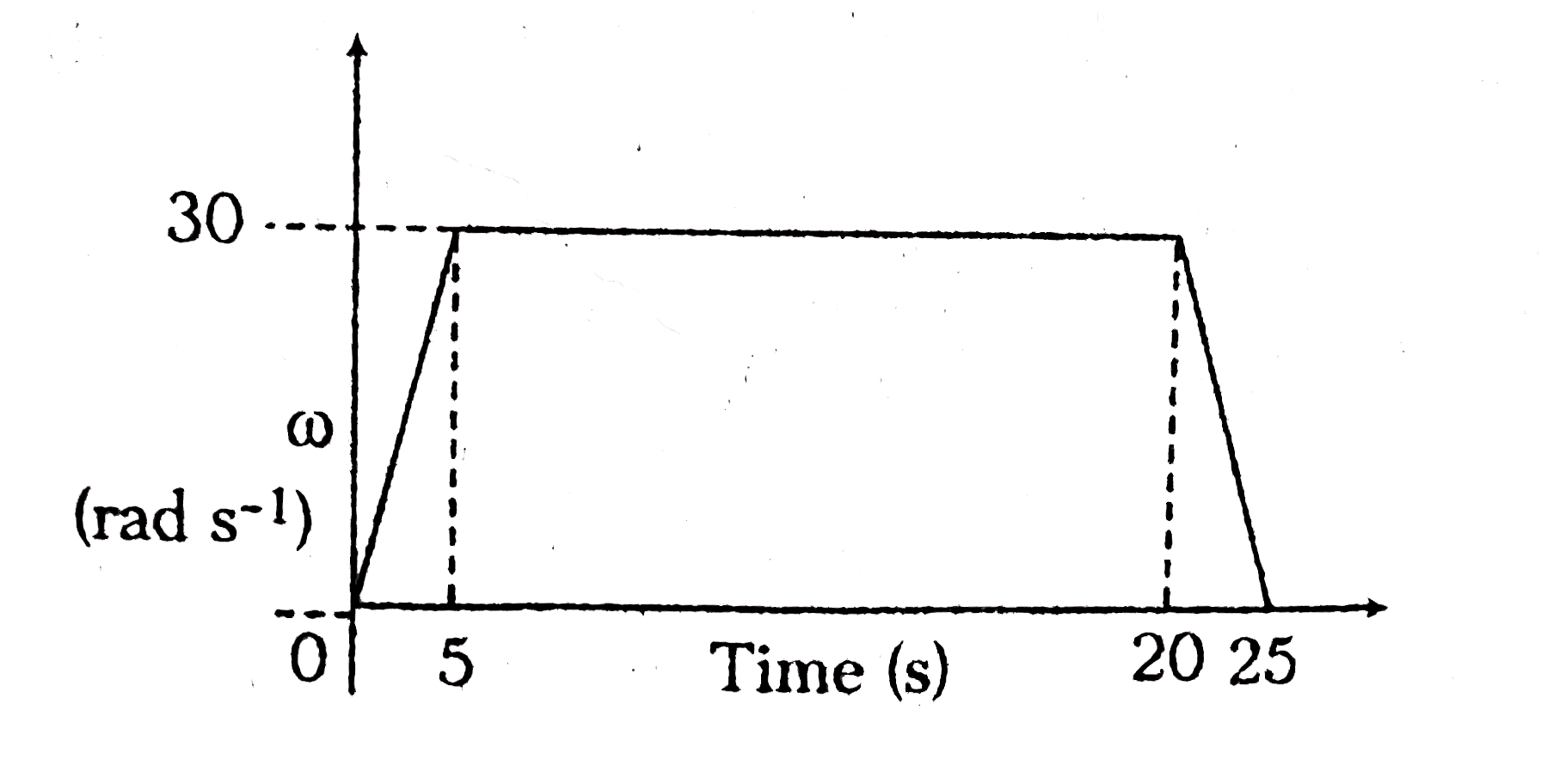
View SolutionThe figure shows the angular velocity versus time graph of a flywheel. The angle, in radians through which the flywheel turns during 25 s is
View SolutionA particle starting from rest attains a velocity of 50ms−1 in 5 s. The acceleration of the particle is
View SolutionA body starts from rest and acquires a velocity 10 m s−1 in 2 s. Find the acceleration.
View Solution
