A particle starting from rest attains a velocity of 50ms−1 in 5 s. The acceleration of the particle is
5ms2
10ms2
50ms2
100ms2
The correct Answer is:B
To find the acceleration of the particle, we can use the first equation of motion, which relates initial velocity, final velocity, acceleration, and time. Here's the step-by-step solution:
Step 1: Identify the given values
- Initial velocity (u) = 0 m/s (since the particle starts from rest)
- Final velocity (v) = 50 m/s
- Time (t) = 5 s
Step 2: Write down the first equation of motion
The first equation of motion is:
v=u+at
where:
- v = final velocity
- u = initial velocity
- a = acceleration
- t = time
Step 3: Substitute the known values into the equation
Substituting the values we have:
50=0+a⋅5
Step 4: Simplify the equation
This simplifies to:
50=5a
Step 5: Solve for acceleration (a)
To find a, divide both sides of the equation by 5:
a=505
Step 6: Calculate the acceleration
Calculating the right side gives:
a=10m/s2
Final Answer
The acceleration of the particle is 10m/s2.
---
- Initial velocity (u) = 0 m/s (since the particle starts from rest)
- Final velocity (v) = 50 m/s
- Time (t) = 5 s
The first equation of motion is:
v=u+at
where:
- v = final velocity
- u = initial velocity
- a = acceleration
- t = time
Substituting the values we have:
50=0+a⋅5
This simplifies to:
50=5a
To find a, divide both sides of the equation by 5:
a=505
Calculating the right side gives:
a=10m/s2
The acceleration of the particle is 10m/s2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two particles of equal mass have velocities v1=2ims−1 and v2=2jms−1 First particle has an acceleration a=(3i+3j)ms−2 while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of
Aa.straight lineBb.parabolaCc.circleDd.ellipse
A train starting from rest attains a velocity of 72km/h in 5 minutes . Assuming that the acceleration is uniform , find (i) the acceleration and (ii) the distance travelled by the train for attaining this velocity .
View SolutionA particle starts from the origin with a velocity of 10ms−1 and moves with a constant acceleration till the velocity increases to 50ms−1. At that instant, the acceleration is suddenly reversed. What will be the velocity of the particle, when it returne to the starticng point?
View SolutionThe acceleration of a'particle starting from rest, varies with time according to the relation a=kt+c. The velocity of the particle after time t will be :
View SolutionA particle moves in the direction of east for 2s with velocity of 15ms−1. Then it moves towards north for 8s with a a velocity of 5ms−1. The average velocity of the particle is
View SolutionA particle starting from rest undergoes a rectilinear motion with acceleration a. The variation of a with time t is shown below. The maximum velocity attained by the particle during its motion is
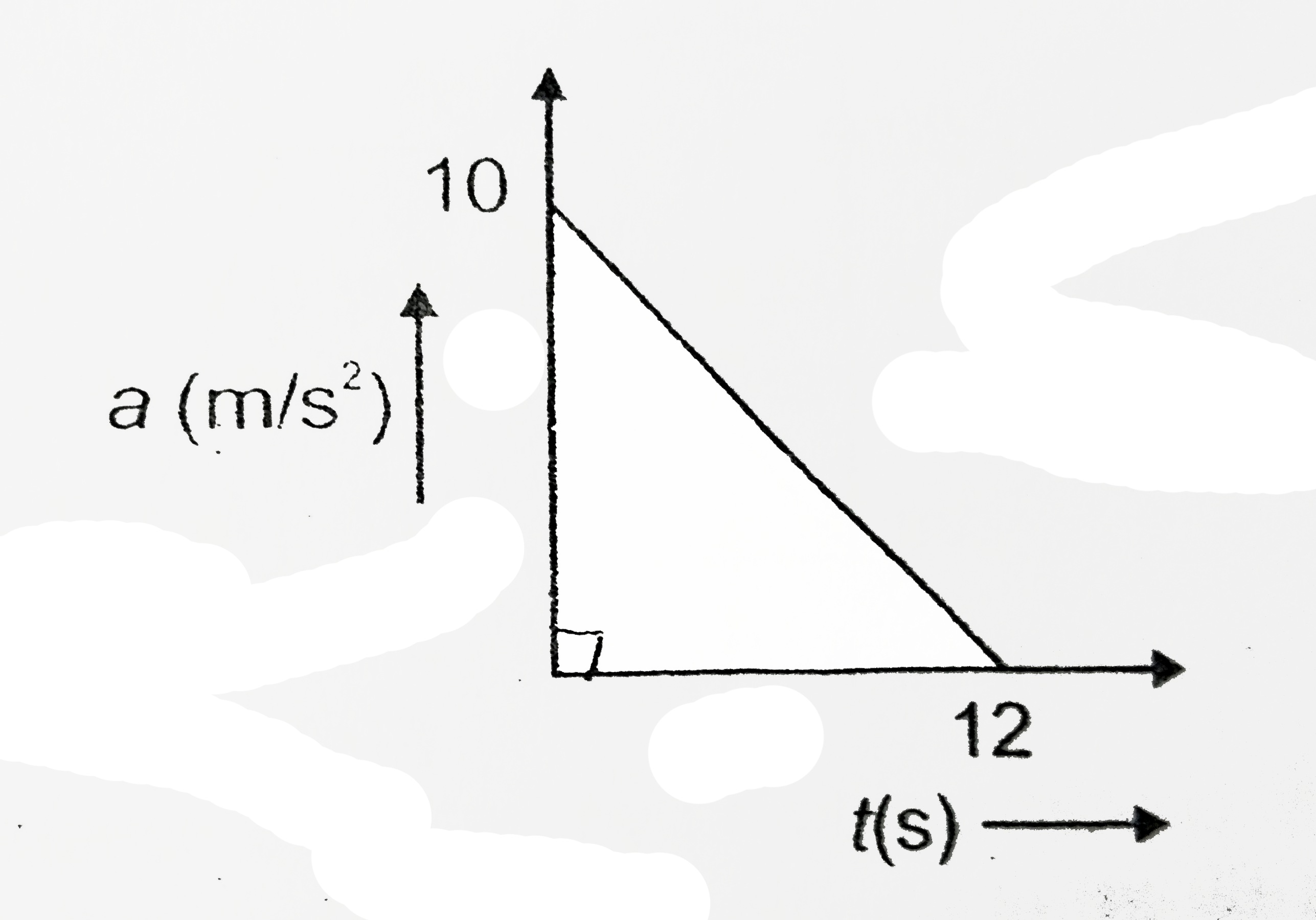
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View Solution
