Two like parallel force 20 N and 30 N act at the ands A and B of a rod 1.5 m long. The resultant of the forces will act at the point
90 cm from A
75 cm from B
20 cm from B
85 cm from A
The correct Answer is:A
To solve the problem, we need to find the point where the resultant of the two parallel forces (20 N and 30 N) acts on a rod of length 1.5 m.
1. Identify the Forces and Their Positions:
- We have two forces:
- F1=20N acting at point A (left end of the rod).
- F2=30N acting at point B (right end of the rod).
- The length of the rod is L=1.5m.
2. Calculate the Resultant Force:
- The resultant force R is the sum of the two forces:
R=F1+F2=20N+30N=50N
3. Determine the Torque About Point A:
- The torque due to a force is given by the formula:
Torque=Force×Perpendicular Distance
- The torque due to the 30 N force about point A is:
τF2=F2×L=30N×1.5m=45N m
- The torque due to the 20 N force about point A is zero since it acts at point A.
4. Set Up the Equation for the Resultant Torque:
- Let x be the distance from point A where the resultant force acts. The torque due to the resultant force about point A is:
τR=R×x=50N×x
5. Equate the Torques:
- Since the torques must be equal for the system to be in equilibrium, we have:
τF2=τR
45N m=50N×x
6. Solve for x:
- Rearranging the equation gives:
x=45N m50N=0.9m=90cm
7. Determine the Distance from Point B:
- The distance from point B to the point where the resultant acts is:
L−x=1.5m−0.9m=0.6m=60cm
Conclusion:
The resultant of the forces will act at a point 90 cm from point A (or 60 cm from point B).
- We have two forces:
- F1=20N acting at point A (left end of the rod).
- F2=30N acting at point B (right end of the rod).
- The length of the rod is L=1.5m.
- The resultant force R is the sum of the two forces:
R=F1+F2=20N+30N=50N
- The torque due to a force is given by the formula:
Torque=Force×Perpendicular Distance
- The torque due to the 30 N force about point A is:
τF2=F2×L=30N×1.5m=45N m
- The torque due to the 20 N force about point A is zero since it acts at point A.
- Let x be the distance from point A where the resultant force acts. The torque due to the resultant force about point A is:
τR=R×x=50N×x
- Since the torques must be equal for the system to be in equilibrium, we have:
τF2=τR
45N m=50N×x
- Rearranging the equation gives:
x=45N m50N=0.9m=90cm
- The distance from point B to the point where the resultant acts is:
L−x=1.5m−0.9m=0.6m=60cm
The resultant of the forces will act at a point 90 cm from point A (or 60 cm from point B).
Similar Questions
A weightless rod is acted upon by two upward parallel forces of 2N and 4N at ends A and B respectively. The total length of the rod AB=3m. To keep the rod in equilibrium a force of 6N should act in the following manner.
View SolutionTwo forces F1=1N and F2=2N act along the lines x=0 and y=0, respectively. Then find the resultant of forces.
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
Two horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
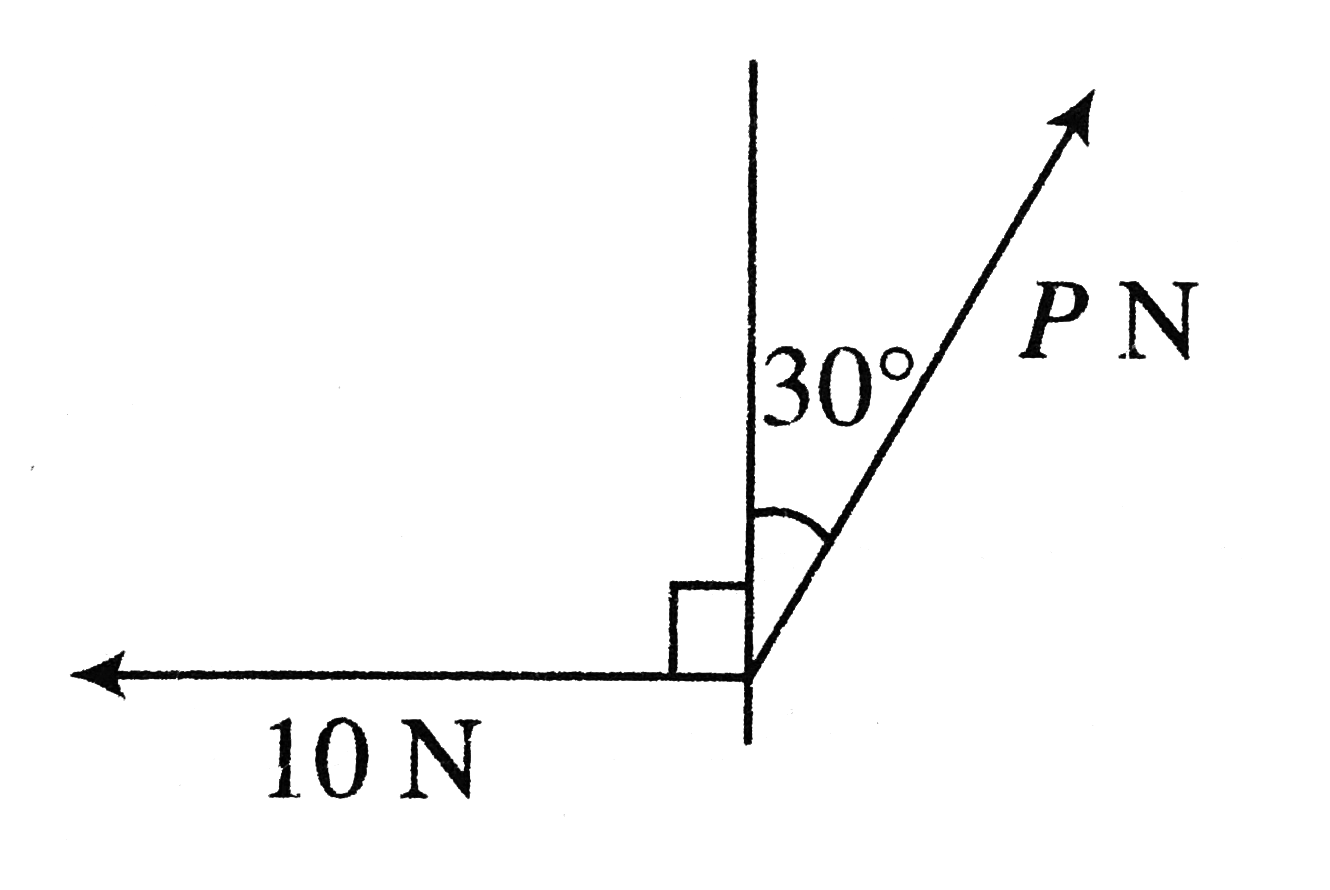
View SolutionTwo non-collinear forces, one of 10 N and another of 6 N act upon a body. The directions of the forces are unknown. The resultant force on the body is :
View SolutionTwo perpendicular forces of magnitudes 10 N and 5 N act at a point. Find their resultant.
View SolutionTwo forces 10 N and 15N aer acting on acting on a body . What can be the maximum and minimum resultant force on the body ?
View SolutionA block is applied two forces of magnitude 5N each. One force is acting towards East and the other acting along 60∘ North of East. The resultant of the two forces (in N) is of magnitude :-
View SolutionTwo forces 12 N and 16 N are acting upon a body, what can be the maximum and minimum resultant force on the body ?
View SolutionThe greatest and least resulant of two forces acting at a point is 10N and 6N,respectively. If each force is increased by 3N, find the resulant of new forces when acting at a point at an angle of 90∘ with each other .
View Solution
