A : When a rigid body rotates about any fixed axis, then all the particles of it move in circles of different radii but with same angular velocity.
R : In rigid body relative position of particles are fixed.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion,
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion,
If Assertion is true statement but Reason is false,
If both Assertion and Reason are false statements,
The correct Answer is:A
Step-by-Step Solution:
1. Understanding the Assertion (A):
- The assertion states that when a rigid body rotates about a fixed axis, all particles of the body move in circles of different radii but with the same angular velocity.
- In a rigid body, the distance between any two particles remains constant during the motion.
2. Visualizing the Rigid Body Rotation:
- Imagine a rigid body (like a spinning disk) rotating around a fixed axis.
- Each particle in the body traces a circular path around the axis of rotation.
- The radius of the circular path for each particle depends on its distance from the axis of rotation.
3. Analyzing the Motion of Particles:
- Let’s consider a few points on the rigid body (e.g., points A, B, C, D).
- Each point will have a different radius (distance from the axis) but will rotate with the same angular velocity (ω).
- This means that while the linear speeds of the particles may differ (due to different radii), their angular speed remains constant.
4. Understanding the Reason (R):
- The reason states that in a rigid body, the relative positions of the particles are fixed.
- This is true because the definition of a rigid body implies that it does not deform during motion; hence, the distances between particles do not change.
5. Conclusion:
- Both the assertion (A) and the reason (R) are true.
- The reason (R) correctly explains the assertion (A) because the fixed relative positions of the particles ensure that they can rotate with the same angular velocity despite having different radii.
6. Final Answer:
- Therefore, the correct option is that both the assertion and reason are true, and the reason is a correct explanation for the assertion.
- The assertion states that when a rigid body rotates about a fixed axis, all particles of the body move in circles of different radii but with the same angular velocity.
- In a rigid body, the distance between any two particles remains constant during the motion.
- Imagine a rigid body (like a spinning disk) rotating around a fixed axis.
- Each particle in the body traces a circular path around the axis of rotation.
- The radius of the circular path for each particle depends on its distance from the axis of rotation.
- Let’s consider a few points on the rigid body (e.g., points A, B, C, D).
- Each point will have a different radius (distance from the axis) but will rotate with the same angular velocity (ω).
- This means that while the linear speeds of the particles may differ (due to different radii), their angular speed remains constant.
- The reason states that in a rigid body, the relative positions of the particles are fixed.
- This is true because the definition of a rigid body implies that it does not deform during motion; hence, the distances between particles do not change.
- Both the assertion (A) and the reason (R) are true.
- The reason (R) correctly explains the assertion (A) because the fixed relative positions of the particles ensure that they can rotate with the same angular velocity despite having different radii.
- Therefore, the correct option is that both the assertion and reason are true, and the reason is a correct explanation for the assertion.
Similar Questions
Knowledge Check
A rigid body rotates about a fixed axis with variable angular velocity equal to (a - bt) at time t where a and b are constants. The angle through which it rotates before it comes to rest is
Aa2bBa22bCa24bDa22b2
A rigid body is free to rotate about an axis. Can the body have non-zero angulalr acceleration of an instant when its angular velocity is zero?
View SolutionS1: Net torque on a system due to all internal force about any point is zero.
S2: For rigid body undergoing fixed axis rotation, the direction of its angular acceleration and angular velocity
S3: if net torque on a rigid body about its centre of mass is zero, the angular speed of the rigid body is always zero.
S4: For a rigid body undergoing fixed axis rotation abouts its centre of mass, then net torque on rigid body about any point is same.
View SolutionA body rotates about a fixed axis with an angular acceleration of 3rad/s2 . The angle rotated by it during the time when its angular velocity increases frm 10 rad/s to 20 rad/s (in radian) is
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
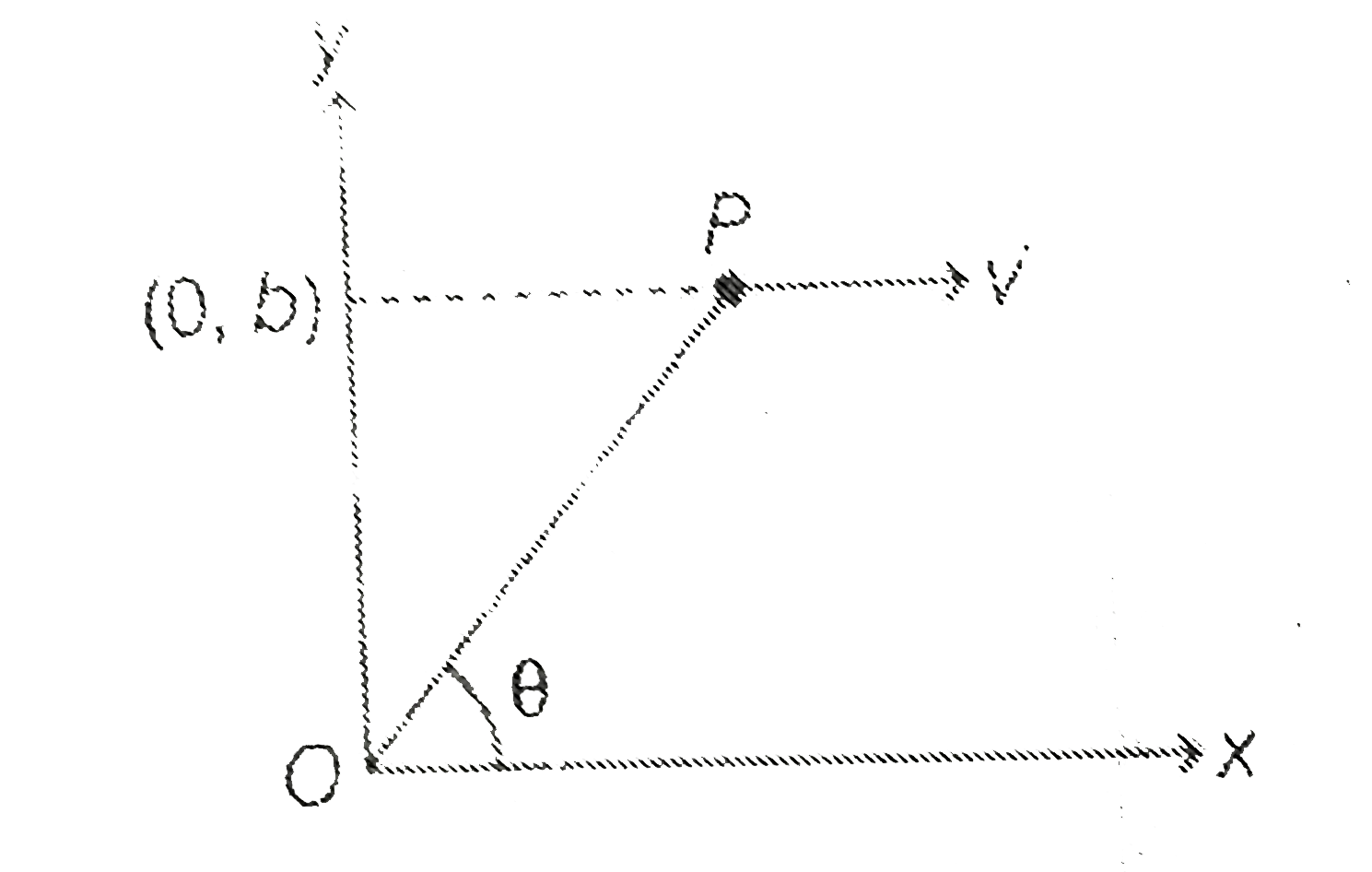
View SolutionA body rotates about a fixed axis with an angular acceleration of one radian/second/second. Through what angle does it rotate during the time in which its angular velocity increases from 5 rad/s to 15 rad/s.
View SolutionA body rotates about a fixed axis with an angular acceleration 1rad/s2 through what angle does it rotates during the time in which its angular velocity increases from 5rad/s to 15rad/s?
View SolutionAll the particles of a rigid rotating body move in a circular path when the axis of rotation:-
View Solution
