Angular momentum of a rigid body rotating about a fixed Axis with angular velocity →ω
is always in the direction of →ω
Is always in the direction perpendicular to →ω
May or may not be in the direction of →ω
Is always in the direction opposite of →ω
To solve the question regarding the angular momentum of a rigid body rotating about a fixed axis with angular velocity →ω, we can follow these steps:
Step 1: Understand the Concept of Angular Momentum
Angular momentum (→L) of a rigid body is a vector quantity that describes the rotational motion of the body. It depends on both the moment of inertia and the angular velocity of the body.
Step 2: Define Angular Momentum Formula
The angular momentum of a rigid body rotating about a fixed axis can be expressed using the formula:
→L=I→ω
where:
- →L is the angular momentum vector,
- I is the moment of inertia of the body about the axis of rotation,
- →ω is the angular velocity vector.
Step 3: Identify the Moment of Inertia
The moment of inertia (I) is a scalar quantity that depends on the mass distribution of the body relative to the axis of rotation. It is calculated by integrating the mass elements of the body with respect to their distance from the axis of rotation.
Step 4: Direction of Angular Momentum
The direction of the angular momentum vector (→L) is the same as the direction of the angular velocity vector (→ω). This means that if the body is rotating in a certain direction, the angular momentum will also point in that same direction.
Step 5: Conclusion
Thus, the angular momentum of a rigid body rotating about a fixed axis with angular velocity →ω is given by:
→L=I→ω
and the direction of →L is the same as that of →ω.
Angular momentum (→L) of a rigid body is a vector quantity that describes the rotational motion of the body. It depends on both the moment of inertia and the angular velocity of the body.
The angular momentum of a rigid body rotating about a fixed axis can be expressed using the formula:
→L=I→ω
where:
- →L is the angular momentum vector,
- I is the moment of inertia of the body about the axis of rotation,
- →ω is the angular velocity vector.
The moment of inertia (I) is a scalar quantity that depends on the mass distribution of the body relative to the axis of rotation. It is calculated by integrating the mass elements of the body with respect to their distance from the axis of rotation.
The direction of the angular momentum vector (→L) is the same as the direction of the angular velocity vector (→ω). This means that if the body is rotating in a certain direction, the angular momentum will also point in that same direction.
Thus, the angular momentum of a rigid body rotating about a fixed axis with angular velocity →ω is given by:
→L=I→ω
and the direction of →L is the same as that of →ω.
Similar Questions
If I, α and τ are the moment of inertia, angular acceleration and torque respectively of a body rotating about an axis with angular velocity ω then,
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity ω. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View Solution
Knowledge Check
Assertion: If the head of a right handed screw rotates with the body, the screw advances in the direction of the angular velocty.
Reason: For rotation about a fixed axis, the angular velocity vector lies along the axis of rotation.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both assertion and reason are false.A rigid body rotates about a fixed axis with variable angular velocity equal to (a - bt) at time t where a and b are constants. The angle through which it rotates before it comes to rest is
Aa2bBa22bCa24bDa22b2A mass is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre with a angular velocity ω0. If the length of the string and angular velocity are doubled, the tension in the string which was initially T0 is now
AT0BT0/2C4T0D8T0
A non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.

View SolutionThe angular momentum of a body with mass (m) moment of inertia (I) and angular velocity (ω) rad/s is equal to
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
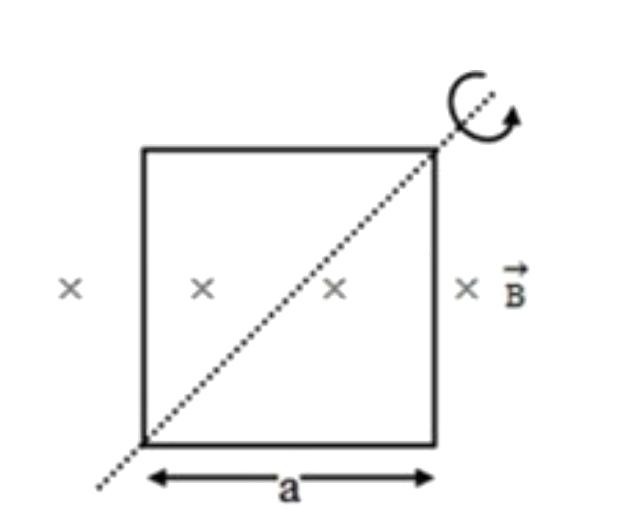
View Solution