A: Lateral strain is directly proportional to the longitudinal strain within the elastic limit.
R:Poission ratio for a given material at a constant temperature is constant.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion,thyen mark(1).
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion,thyen mark(2).
If Assertion is true statement but Reason is false,then mark(3).
If both Assertion and Reason are false statement,then mark(4).
To solve the question, we need to analyze the assertion and the reason provided:
Assertion (A): Lateral strain is directly proportional to the longitudinal strain within the elastic limit.
Reason (R): Poisson's ratio for a given material at a constant temperature is constant.
1. Understanding Lateral and Longitudinal Strain:
- When a material is subjected to an axial load, it experiences a change in length (longitudinal strain) and a change in dimensions perpendicular to the load (lateral strain).
- Within the elastic limit, as the longitudinal strain increases (due to stretching), the lateral strain also increases as the material tries to maintain its volume.
2. Establishing the Relationship:
- The relationship between lateral strain and longitudinal strain can be expressed mathematically as:
Lateral Strain=−Poisson's Ratio×Longitudinal Strain
- This indicates that lateral strain is directly proportional to longitudinal strain, confirming the assertion.
3. Understanding Poisson's Ratio:
- Poisson's ratio (ν) is defined as the ratio of lateral strain to longitudinal strain:
ν=Lateral StrainLongitudinal Strain
- For a given material at a constant temperature, Poisson's ratio remains constant, which implies that the proportionality between lateral and longitudinal strain holds true.
4. Conclusion:
- Both the assertion and the reason are true.
- The reason (Poisson's ratio being constant) correctly explains why lateral strain is directly proportional to longitudinal strain within the elastic limit.
Final Answer:
- Since both the assertion and reason are true, and the reason is the correct explanation of the assertion, the answer is Option 1.
---
- When a material is subjected to an axial load, it experiences a change in length (longitudinal strain) and a change in dimensions perpendicular to the load (lateral strain).
- Within the elastic limit, as the longitudinal strain increases (due to stretching), the lateral strain also increases as the material tries to maintain its volume.
- The relationship between lateral strain and longitudinal strain can be expressed mathematically as:
Lateral Strain=−Poisson's Ratio×Longitudinal Strain
- This indicates that lateral strain is directly proportional to longitudinal strain, confirming the assertion.
- Poisson's ratio (ν) is defined as the ratio of lateral strain to longitudinal strain:
ν=Lateral StrainLongitudinal Strain
- For a given material at a constant temperature, Poisson's ratio remains constant, which implies that the proportionality between lateral and longitudinal strain holds true.
- Both the assertion and the reason are true.
- The reason (Poisson's ratio being constant) correctly explains why lateral strain is directly proportional to longitudinal strain within the elastic limit.
- Since both the assertion and reason are true, and the reason is the correct explanation of the assertion, the answer is Option 1.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-C)29videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J9videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - Mock test 03EXERCISE - EXAMPLE44videos
Mock test 03
Similar Questions
Within the elastic limit, stress is directly proportional to strain produced in a body is the statement of
View SolutionAssertion : The pressure of a gas is inversely proportional to its volume at constant temperature and n.
Reason : The gas volume is directly proportional to n at constant temperature and pressure .View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe isView SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe isView SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe isView SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
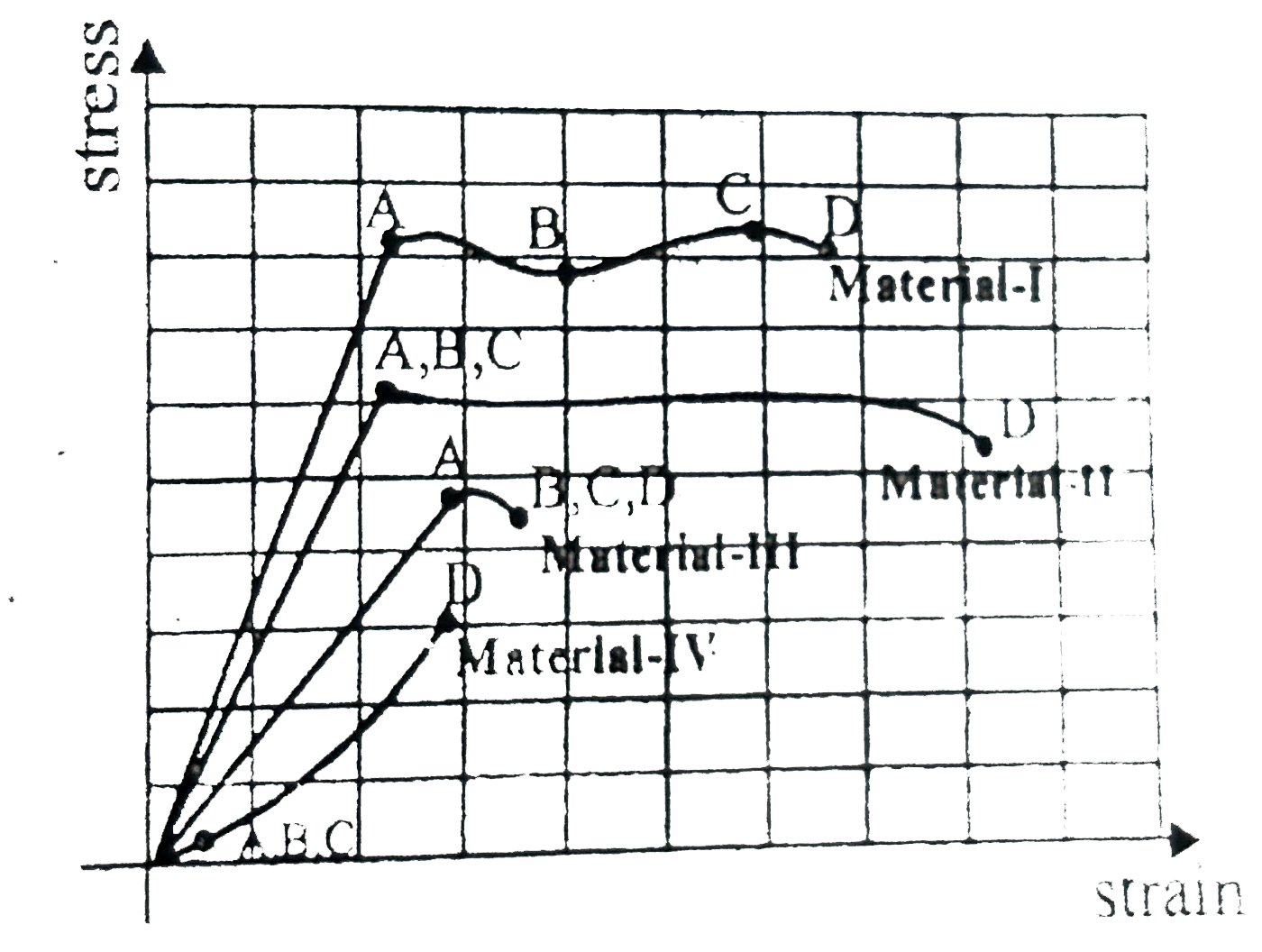
Material which is good for making wires by stretching isView SolutionGiven that the marginal cost MC and average cost AC of a product are directly proportional to each other. Prove that total cost function is C(x)=kxλ , where k is integration constant and 2 is variation constant.
View SolutionStatement-1 : The value of moduli of elasticity is directly proportional to stress.
Statement-2 : The value of moduli of elasticity is inversely proportional to strain.
Statement-3 : The value of moduli of elasticiy is independent of magnitude of stress and strain.View SolutionAssertion : The pressure of a given mass of a gas is directly proportional to the temperature on kelvin scale at constant volume
Reason : With the increase in temperature, the average kinetic energy and hence the average velocity of the molecule increasesView SolutionThe following figure shows the variation of intensity of magnetisation I versus the applied magnetic field intensity H, for two magnetic materials A and B
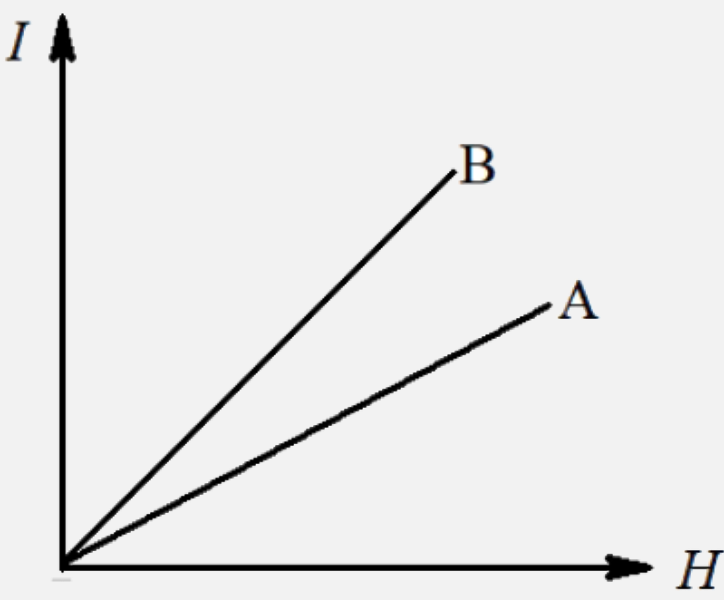
Which of the material have a larger susceptibility for a given field at constant temperature?View Solution

