Prove that the average pressure of a liquid (density ρ) on the walls of the container filled upto height h with liquid is 12hρg.
To prove that the average pressure of a liquid (density ρ) on the walls of a container filled up to height h with liquid is given by Pavg=12hρg, we can follow these steps:
Step 1: Understand the Setup
Consider a vertical cylindrical container filled with a liquid to a height h. The liquid has a density ρ.
Step 2: Define the Pressure at a Depth
The pressure at a depth x from the surface of the liquid is given by the hydrostatic pressure formula:
P(x)=ρgx
where g is the acceleration due to gravity.
Step 3: Consider a Differential Element
Take a small horizontal strip of the wall of the container at depth x with thickness dx. The area of this strip is:
dA=2πrdx
where r is the radius of the cylindrical container.
Step 4: Calculate the Differential Force
The differential force dF acting on this strip due to the pressure is:
dF=P(x)⋅dA=(ρgx)⋅(2πrdx)
Thus,
dF=2πrρgxdx
Step 5: Integrate to Find Total Force
To find the total force F acting on the walls of the container, integrate dF from x=0 to x=h:
F=∫h0dF=∫h02πrρgxdx
Calculating the integral:
F=2πrρg(x22)h0=2πrρg(h22)=πrρgh2
Step 6: Calculate the Total Area
The total area A of the walls of the container up to height h is:
A=2πrh
Step 7: Calculate Average Pressure
The average pressure Pavg on the walls of the container is given by the total force divided by the total area:
Pavg=FA=πrρgh22πrh
Simplifying this expression:
Pavg=ρgh22h=12ρgh
Conclusion
Thus, we have proved that the average pressure of the liquid on the walls of the container is:
Pavg=12hρg
Consider a vertical cylindrical container filled with a liquid to a height h. The liquid has a density ρ.
The pressure at a depth x from the surface of the liquid is given by the hydrostatic pressure formula:
P(x)=ρgx
where g is the acceleration due to gravity.
Take a small horizontal strip of the wall of the container at depth x with thickness dx. The area of this strip is:
dA=2πrdx
where r is the radius of the cylindrical container.
The differential force dF acting on this strip due to the pressure is:
dF=P(x)⋅dA=(ρgx)⋅(2πrdx)
Thus,
dF=2πrρgxdx
To find the total force F acting on the walls of the container, integrate dF from x=0 to x=h:
F=∫h0dF=∫h02πrρgxdx
Calculating the integral:
F=2πrρg(x22)h0=2πrρg(h22)=πrρgh2
The total area A of the walls of the container up to height h is:
A=2πrh
The average pressure Pavg on the walls of the container is given by the total force divided by the total area:
Pavg=FA=πrρgh22πrh
Simplifying this expression:
Pavg=ρgh22h=12ρgh
Thus, we have proved that the average pressure of the liquid on the walls of the container is:
Pavg=12hρg
Similar Questions
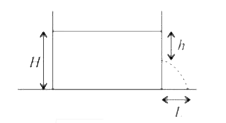
A liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
 View Solution
View SolutionTwo identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid heigth is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View Solution
Knowledge Check
- Question 1 - Select One
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ - Question 2 - Select One
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
When a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature in this process remains constant.)
 View Solution
View SolutionWhen a vertical capillary of length with the sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature this process remains constant.)
 View Solution
View SolutionIf liquid of density ρ is filled in an open cylindrical container to height h, then pressure at bottom
View SolutionA container contains an incompressible and non - viscous liquid of density ρ and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .
 View Solution
View SolutionA container of large uniform cross sectional area A, resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density d and 2d, each of height H2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A tiny hole of area (s(s<<A) is punched on the vertical side of the container at a height h(h<H2). Determine

The horizontal distance traveled by the liquid, initially, is :View SolutionA container of large uniform cross sectional area A, resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density d and 2d, each of height H2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A tiny hole of area (s(s<<A) is punched on the vertical side of the container at a height h(h<H2). Determine

the initial speed of efflux of the liquid at the holeView Solution

