Water stands upto a height behind the vertical wall of a dam what is the net horizontal force pushing the dam down by the stream if width of the dam is ? density of water)
To solve the problem of finding the net horizontal force acting on the dam due to water standing up to a height h, we can follow these steps:
1. Understand the Setup:
- We have a vertical wall of a dam with height h and width σ.
- The water exerts pressure on the dam due to its height.
2. Consider a Differential Element:
- Take a small horizontal strip of the dam at a height y from the top, with a small height dy.
- The area of this differential strip dA is given by:
dA=σ⋅dy
3. Calculate the Pressure at Height y:
- The pressure P at a depth y is given by the hydrostatic pressure formula:
P=ρgy
- Here, ρ is the density of water and g is the acceleration due to gravity.
4. Determine the Differential Force dF:
- The differential force dF acting on the differential area dA is:
dF=P⋅dA=(ρgy)⋅(σ⋅dy)
- Thus, we have:
dF=ρgσydy
5. Integrate to Find the Total Force F:
- To find the total force acting on the dam, integrate dF from y=0 to y=h:
F=∫h0dF=∫h0ρgσydy
6. Perform the Integration:
- The integral can be computed as follows:
F=ρgσ∫h0ydy=ρgσ(y22)h0=ρgσ⋅h22
7. Final Result:
- Therefore, the net horizontal force acting on the dam is:
F=12ρgσh2
Conclusion:
The net horizontal force pushing the dam down by the stream is given by:
F=12ρgσh2
- We have a vertical wall of a dam with height h and width σ.
- The water exerts pressure on the dam due to its height.
- Take a small horizontal strip of the dam at a height y from the top, with a small height dy.
- The area of this differential strip dA is given by:
dA=σ⋅dy
- The pressure P at a depth y is given by the hydrostatic pressure formula:
P=ρgy
- Here, ρ is the density of water and g is the acceleration due to gravity.
- The differential force dF acting on the differential area dA is:
dF=P⋅dA=(ρgy)⋅(σ⋅dy)
- Thus, we have:
dF=ρgσydy
- To find the total force acting on the dam, integrate dF from y=0 to y=h:
F=∫h0dF=∫h0ρgσydy
- The integral can be computed as follows:
F=ρgσ∫h0ydy=ρgσ(y22)h0=ρgσ⋅h22
- Therefore, the net horizontal force acting on the dam is:
F=12ρgσh2
The net horizontal force pushing the dam down by the stream is given by:
F=12ρgσh2
Similar Questions
Water stands at a depth D behind the vertical upstream face of a dam as shown in the figure. The force exerted on the dam by water per unit width is

View SolutionWater stands at a depth h behind the vertical face of a dam. It exerts a resultant horizontal force on the dam tendibg to slide it along its foundation and a torque tending to overturn the dam about the point O. Find

(a) Horizontal force,(b) torque about O, (c ) the height at which the resultant force would have to act to produce the same torque,l=cross-sectional length and ρ=density of water.
View Solution
Knowledge Check
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water assuming that it does not rebound? (Density of water =1000kgm−3)
A1.25×103NB2.25×103NC3.25×103ND4.25×103N
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall near by what is the force exerted on the wall by the impact of water assuming.that it does not rebound? (Density of water =1000kgm3)
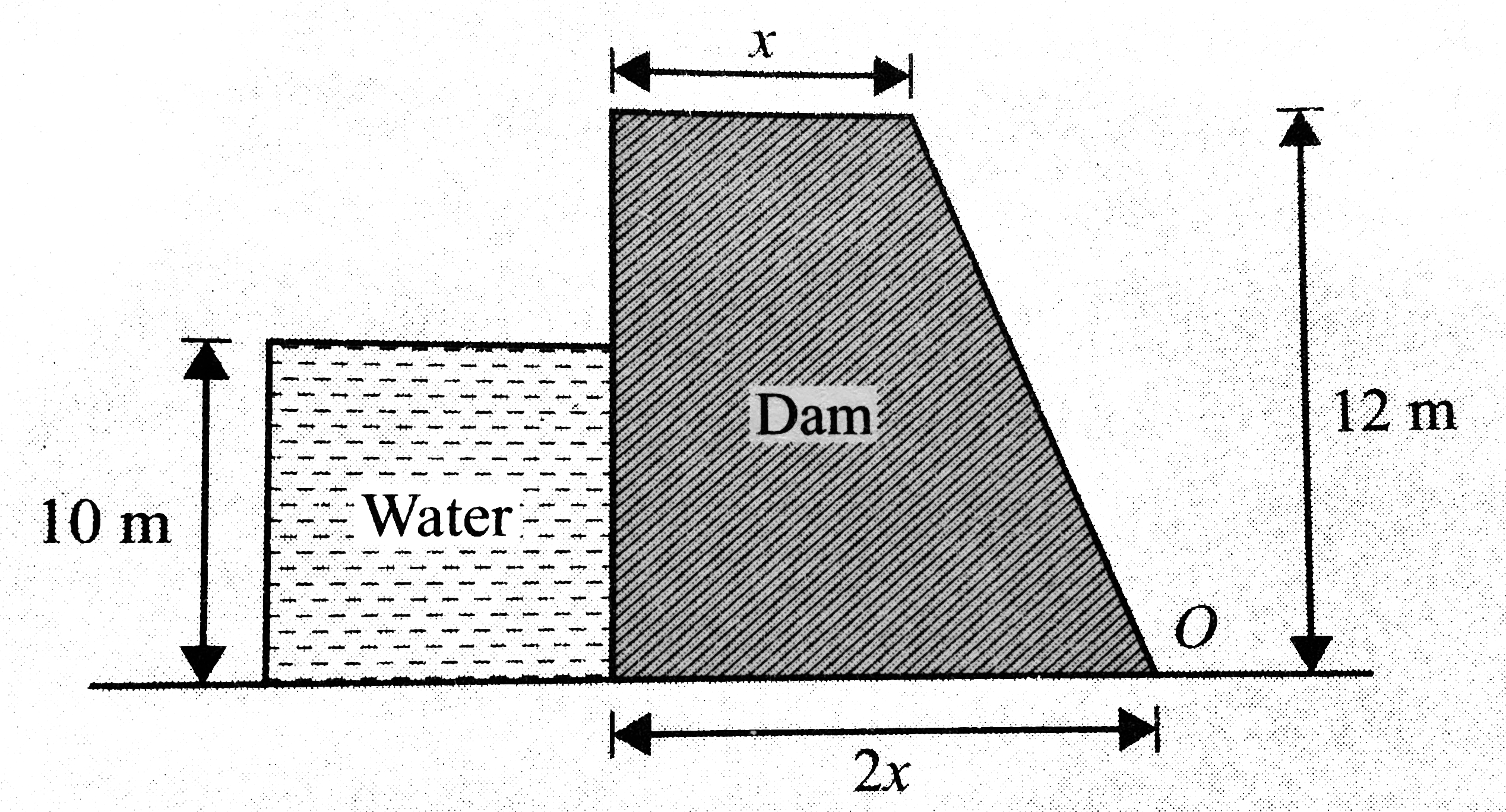
View SolutionFigure shows a cross sectional view of a masonry dam whose length perpendiclar to te diagram is 30m. The depth of the water behind te dam is 10m. the masonry of which is the dam is constructed has a density of 3000kg/m3.
a. Find the dimensions x and 2x if the weight of the dam is to be 10 times the horizontal force exerted on it by water.
b. Check the stability of the dam with respect to its overturning about the edge through point O.
View SolutionA sperical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is [ρ is the density of water]-
View SolutionTwo cyllindrical vessels of equal cross sectional ara A contain water upto heights h1 and h2. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is ρ
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg = 10 ms^(-2)).
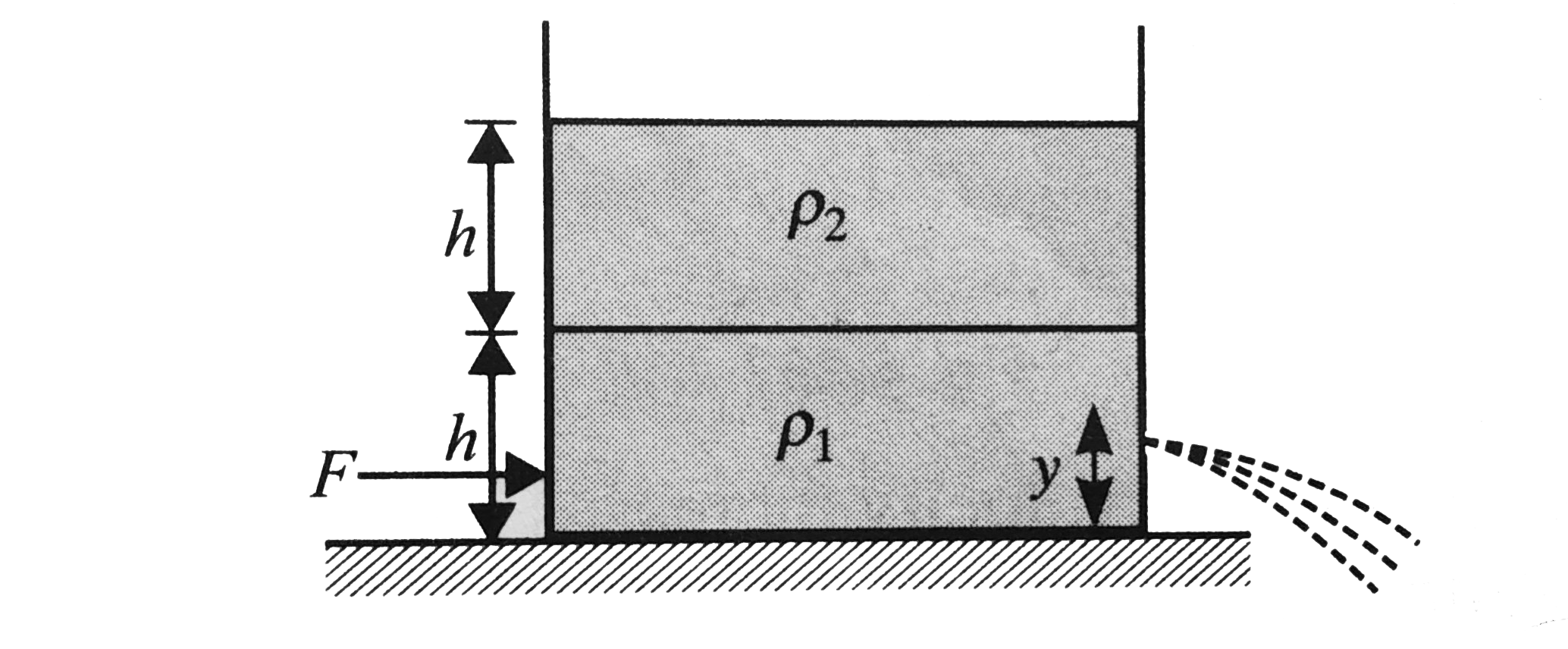
The horizontal force required to keep the cylinder in static equilibrium, on a smooth horizontal plane is
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (Take g = 10 ms^(-2)).
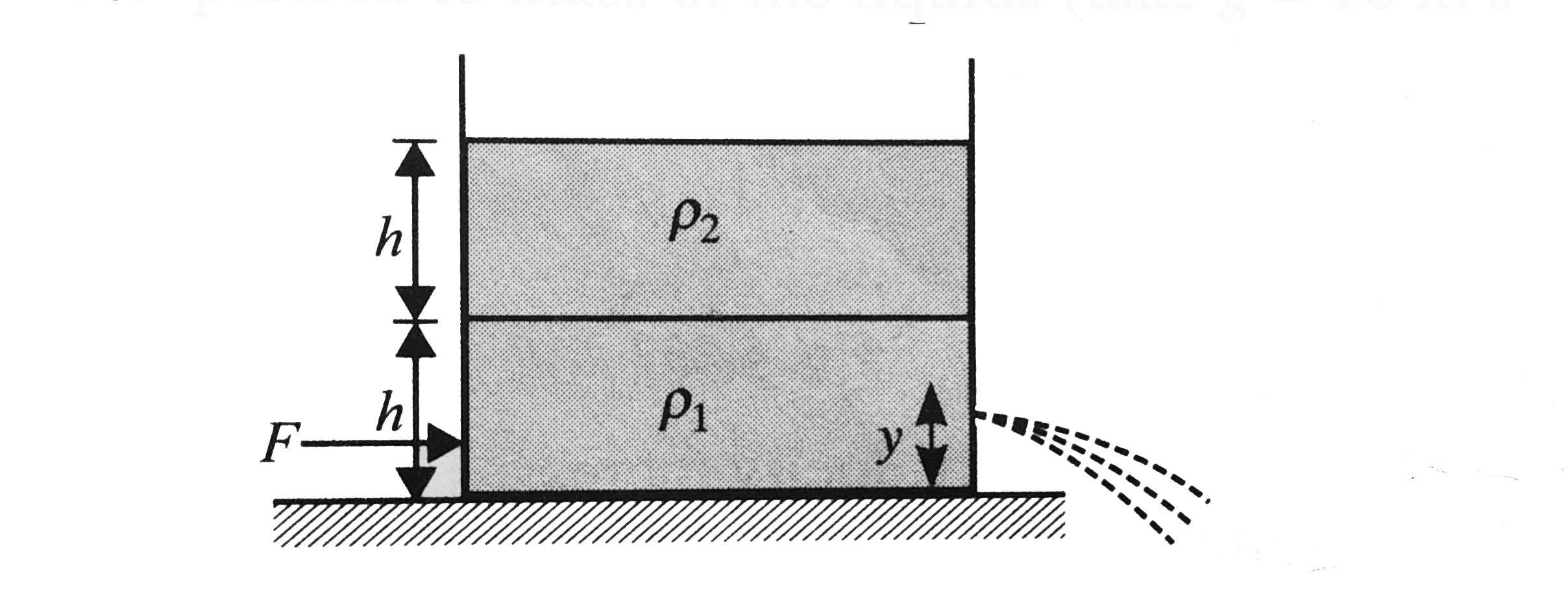
The velocity of efflux is
View SolutionThe height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is

View Solution