Water stands upto height h behind the dam as shown in the figure. The front view of the dam gate is also shown in the adjoining figure. Density of water is ρ and acceleration due to gravity is g. If atmospheric pressure force is also considered, then the point of application of total force acting on the dam due to water above O is

hrr4r
h3
h
h2
The correct Answer is:B
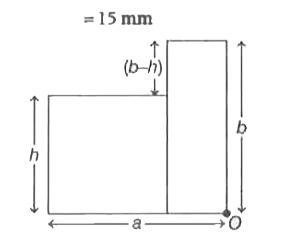
Force on dam = Pressure of water × Area = {(density of water) (acceleration due to gravity) (height of water/2} × {(width of dam) (height of water)}
F=(ρg(h)2)×[(b−h).h]
=ρg2(bh2−h3)
At equilibrium, atmospheric pressure = pressure on dam
So, dFdh=0
⇒∂∂h{ρg2(bh2−h3)}=0
⇒ρg2(2bh−3h2)=0
⇒2bh−3h2=0
⇒2b=3h⇒b=3h/2
b−h=3h2−h=h/2 is the location where the total weight of water acts at a particular point.
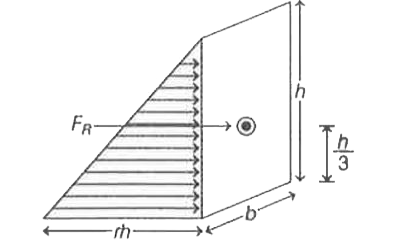
To find the point of action of total force,
yR=IxcycA+yc
where, yR= location where point of force acts, A = area,
yc= location where total weight acts = h/2 and Ixc = moment of inertia (here rectangular plate).
=112Ah2=112bh3
so, yR=(1/12)bh3(1/2)h.bh+12h
=16h+12h=23h (from the top)
So, yR=h3 (above the base) =23h (from the top)
Topper's Solved these Questions
- AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)EXERCISE - Physics
40 Videos
- AP EAMCET SOLVED PAPER 2019BOOK - TS EAMCET PREVIOUS YEAR PAPERSCHAPTER - AP EAMCET SOLVED PAPER 2019EXERCISE - PHYSICS
40 Videos
Similar Questions
Water stands at a depth D behind the vertical upstream face of a dam as shown in the figure. The force exerted on the dam by water per unit width is

View SolutionWater is filled up to a height h in a beaker of radius R as shown in the figure. The density of water is ρ, the surface tension of water is T and the atmospheric pressure is P0. Consider a vertical section ABCD of the water column through a diameter of the beaker. The force on water on one side of this section by water on the other side of this section has magnitude

View Solution
Knowledge Check
Water stands at a depth D behind the vertical upstream face of a dam as shown in the figure. The force exerted on the dam by water per unit width is
 A13ρgD2B12ρgD2C13ρgDD12(ρgD)2
A13ρgD2B12ρgD2C13ρgDD12(ρgD)2Water stands upto a height h behind the vertical wall of a dam what is the net horizontal force pushing the dam down by the stream if width of the dam is σ? (ρ= density of water)
A2hσgBh2σρg2Ch2σρg4Dhσρg4A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceA∣∣2P0Rh+πR2ρgh−2RT∣∣B∣∣2P0Rh+Rρgh2−2RT∣∣C∣∣P0πR2+Rρgh2−2RT∣∣D∣∣P0πR2+Rρgh2−2RT∣∣
Water stands upto a height h behind the vertical wall of a dam what is the net horizontal force pushing the dam down by the stream if width of the dam is σ? (ρ= density of water)
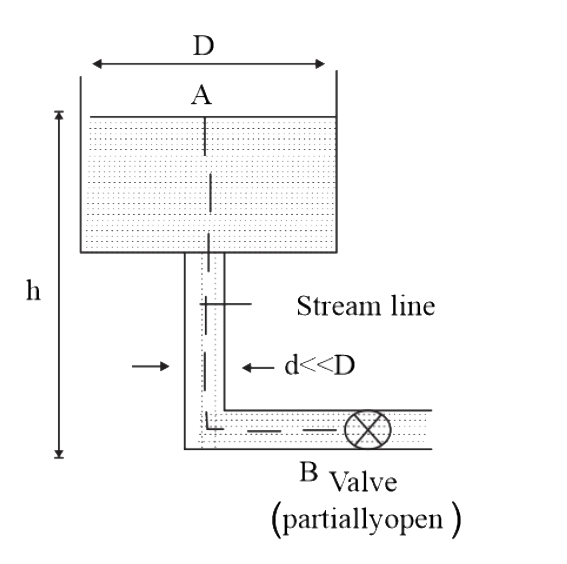
View SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
View SolutionWater is filled up to a height h in a beaker of radiys R as shown in the figure. The density of water is ρ, the surface tension of water is T and the atmospheric pressure is P0. Consider a vertical section ABCD of the water column through a diameter of the beaker. The force on water on one side on this section by water on the other side of this section has magnitude

View SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -

View SolutionSwimming is an interesting sport, and one that relaxes us also. Normally and average human being would drown in water.As a person goes inside water , the water exert a force on it in upwared direction. This force is called buyont froce. The force is given by V dg, where d is density of water, V is volume of body inside water and g is acceleration due to gravity. normally, this force is lesser than this weight. so the man pushes water to get an additional force on himself. this effort is known as swimming. assume water has a density of 1000kg/m3
If a sphere is resting on the ocean floor, its free body diagram would be
View Solution
