An object of mass m is floating in a liquid of density σ. If the object is made up of density ρ, then appare weight of the object in the liquid is
mg
mg(1−σρ)
mg(1−ρσ)
Zero
To find the apparent weight of an object floating in a liquid, we can follow these steps:
Step 1: Understand the forces acting on the object
The object has two main forces acting on it:
1. The true weight (W) acting downwards, which is given by:
W=mg
where m is the mass of the object and g is the acceleration due to gravity.
2. The buoyant force (B) acting upwards, which is given by Archimedes' principle. The buoyant force is equal to the weight of the liquid displaced by the object:
B=σVg
where σ is the density of the liquid, V is the volume of the object submerged in the liquid, and g is the acceleration due to gravity.
Step 2: Relate the volume of the object to its mass and density
The volume V of the object can be expressed in terms of its mass m and its density ρ:
V=mρ
Step 3: Substitute the volume into the buoyant force equation
Substituting V into the buoyant force equation gives:
B=σ(mρ)g
Step 4: Write the equation for apparent weight
The apparent weight W′ of the object in the liquid is given by the true weight minus the buoyant force:
W′=W−B
Substituting the expressions for W and B:
W′=mg−σ(mρ)g
Step 5: Factor out common terms
Factoring out mg from the equation:
W′=mg(1−σρ)
Final Answer
Thus, the apparent weight of the object in the liquid is:
W′=mg(1−σρ)
The object has two main forces acting on it:
1. The true weight (W) acting downwards, which is given by:
W=mg
where m is the mass of the object and g is the acceleration due to gravity.
B=σVg
where σ is the density of the liquid, V is the volume of the object submerged in the liquid, and g is the acceleration due to gravity.
The volume V of the object can be expressed in terms of its mass m and its density ρ:
V=mρ
Substituting V into the buoyant force equation gives:
B=σ(mρ)g
The apparent weight W′ of the object in the liquid is given by the true weight minus the buoyant force:
W′=W−B
Substituting the expressions for W and B:
W′=mg−σ(mρ)g
Factoring out mg from the equation:
W′=mg(1−σρ)
Thus, the apparent weight of the object in the liquid is:
W′=mg(1−σρ)
Similar Questions
Knowledge Check
A body of weight W is floating in a liquid. Its apparent weight will be :
Aequal to WBless than WCgreater than WDzeroThe pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
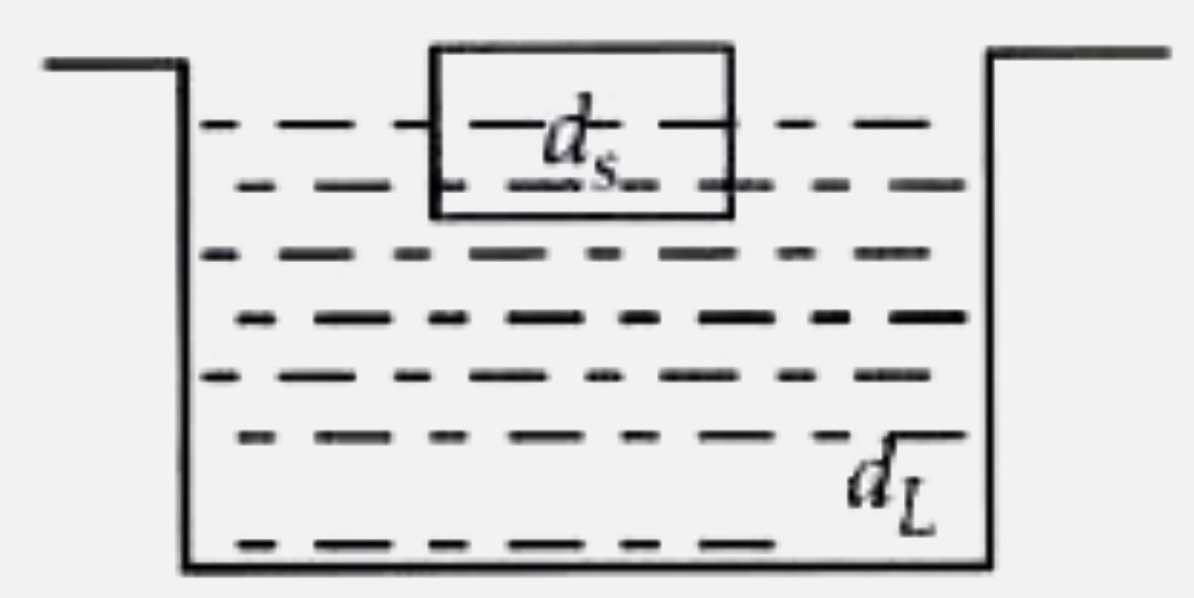
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the apparent weight of the floating body?
View SolutionA solid of density D is floating in a liquid of density d. If υ is the volume of solid submerged in the liquid and V is the total volume of the solid, then υ/V equal to
View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View SolutionAn object is floating in a liquid , kept in a container . The container is placed in a lift . Choose the correct option .
View Solution_E01_052_Q01.png)
An object of volume V is submerged in a liquid of density ρ. It has flat bottom of area A which is at depth of H in the liquid and a dome shaped top find the total force of liquid acting on the top of the object.
View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View Solution
