A liquid of density 103kgm3 and coefficient of viscosity 8 xx10^(-2) decapoise is flowing in a tube of radius 2 cm with speed 2 m/s. The. Reynold’s number is
500
1000
1500
2000
To find the Reynolds number for the given fluid flow, we will use the formula:
Re=ρvdη
where:
- Re is the Reynolds number,
- ρ is the density of the fluid (in kg/m³),
- v is the velocity of the fluid (in m/s),
- d is the diameter of the tube (in meters),
- η is the coefficient of viscosity (in Pa·s or N·s/m²).
Step 1: Identify the given values
- Density, ρ=103kg/m3=1000kg/m3
- Velocity, v=2m/s
- Radius of the tube, r=2cm=0.02m
- Coefficient of viscosity, η=8×10−2decapoise
Step 2: Convert the radius to diameter
The diameter d of the tube is given by:
d=2r=2×0.02m=0.04m
Step 3: Convert the coefficient of viscosity to SI units
1 decapoise is equal to 0.1Pa⋅s. Thus,
η=8×10−2decapoise=8×10−2×0.1Pa⋅s=8×10−3Pa⋅s
Step 4: Substitute the values into the Reynolds number formula
Now we can substitute the values into the Reynolds number formula:
Re=(1000kg/m3)(2m/s)(0.04m)8×10−3Pa⋅s
Step 5: Calculate the Reynolds number
Calculating the numerator:
1000×2×0.04=80kg/(m⋅s)
Now substituting this into the formula:
Re=808×10−3=800.008=10000
Final Answer
The Reynolds number Re is:
Re=10000
- Re is the Reynolds number,
- ρ is the density of the fluid (in kg/m³),
- v is the velocity of the fluid (in m/s),
- d is the diameter of the tube (in meters),
- η is the coefficient of viscosity (in Pa·s or N·s/m²).
- Density, ρ=103kg/m3=1000kg/m3
- Velocity, v=2m/s
- Radius of the tube, r=2cm=0.02m
- Coefficient of viscosity, η=8×10−2decapoise
The diameter d of the tube is given by:
d=2r=2×0.02m=0.04m
1 decapoise is equal to 0.1Pa⋅s. Thus,
η=8×10−2decapoise=8×10−2×0.1Pa⋅s=8×10−3Pa⋅s
Now we can substitute the values into the Reynolds number formula:
Re=(1000kg/m3)(2m/s)(0.04m)8×10−3Pa⋅s
Calculating the numerator:
1000×2×0.04=80kg/(m⋅s)
Now substituting this into the formula:
Re=808×10−3=800.008=10000
The Reynolds number Re is:
Re=10000
Similar Questions
A liquid of coefficient of viscosity η=1 poise is flowing in a pipe of radius 3 cm such that the rate of volume flow is 1000l/min.Determine the Reynolds numbers. (A) 3536 (B) 3500 (C) 3400 (D) 3600
View SolutionA drop of water of radius 10−5m is falling through a medium whose density is1.21kgm−3 and coefficient of Viscosity 1.8×10−4 poise. Find the terminal velocity of the drop.
View SolutionTo what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
View SolutionA spherical ball of diameter 1 cm and density 5×103kgm−3 is dropped gently in a large tank containing viscous liquid of density 3×103kgm−3 and coefficient of viscosity 0.1Nsm−2. The distance that the ball moves n 1 s after attaining terminal velocity is (g=10ms−2)
View SolutionVolume rate flow of a liquid of density ρ and coefficient of viscosity η through a cylindrical tube of diameter D is Q. Reynold's number of the flow is
View SolutionA liquid having coefficient of viscosity 0.02 decapoise is filled in a container of cross-sectional area 20 m^2 viscous drag between two adjacent layers in flowing is 1 N, then velocity gradient is
View SolutionCompute the terminal velocity of a rain drop of radius 0.3 mm. Take coefficient of viscosity of air 1.83X10−5 poise and density of air = 1.3kgm−3 Density of water - 103kgm−3andtakeg=9.8ms−2
View SolutionA liquid of density ρ=1000kg/m3 viscosity η=0.1Ns/m2 is flowing down in vertical pipe of large cross section. A small ball of density ρ0=100kg/m3 and r=5cm will be at rest in flowing liquid, if velocity of flowing liquid is 10km/s. Then find the value of k.

View SolutionWater flows at a speed of 6 cms−1 through a tube of radius 1 cm. coefficient of viscosity of water at room temperature is 0.01 poise. Calculate the Reynolds number. Is it a steady flow.
View SolutionA non viscous liquid of constant density 103kg/m3 flows in stream line motion along a vertical tube PQ of variable cross-section. Height of P and Q are 2m and 2.5m respectively. Area of tube at Q is equal to 3 times the area of tube at 'P'. Then work done per unit volume by pressure as liquid flows from P and Q. Speed of liquid at 'P' is 3m/s.
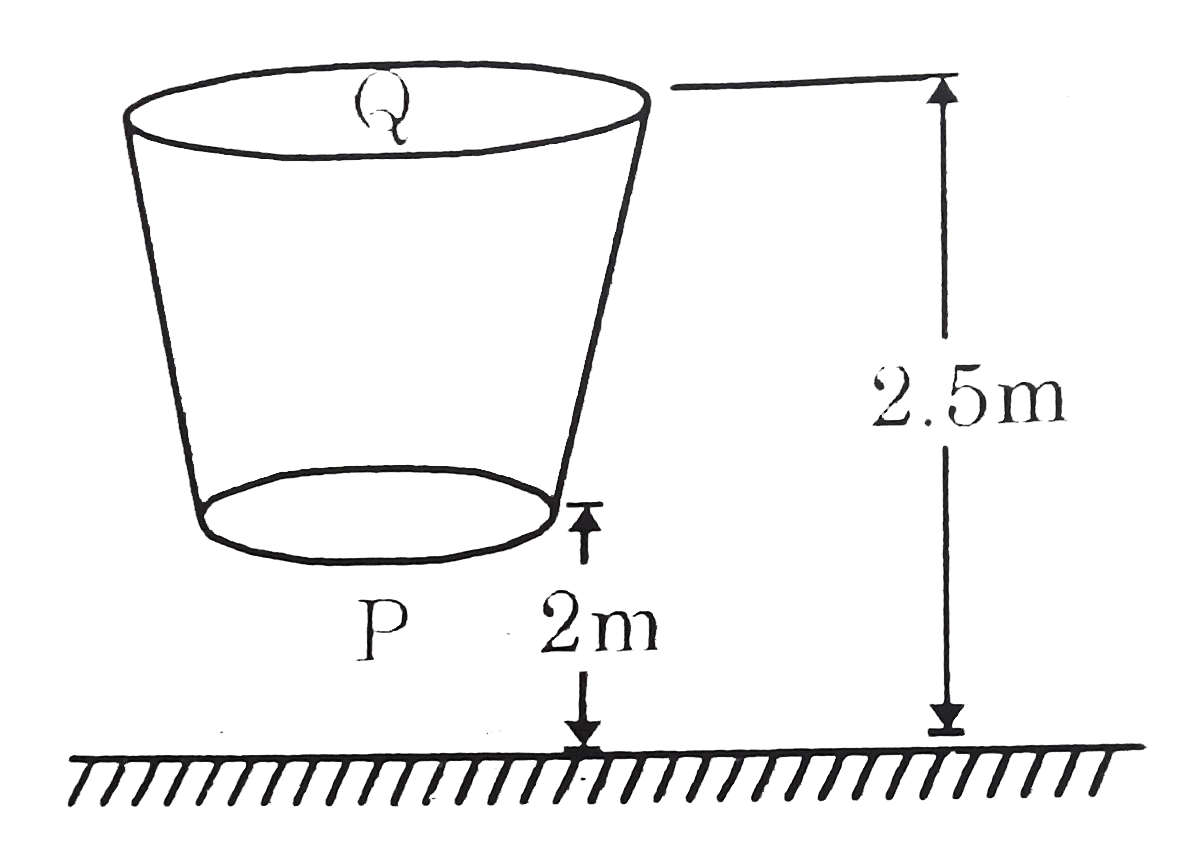
View Solution
