To what height does a liquid of density kg and surface tension 0.05 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given ]
25 cm
15 cm
5 cm
20 cm
The correct Answer is:C
To find the height to which a liquid rises in a capillary tube, we can use the formula for capillary rise:
h=2TcosθρgR
Where:
- h = height of the liquid column
- T = surface tension of the liquid
- θ = angle of contact
- ρ = density of the liquid
- g = acceleration due to gravity
- R = radius of the capillary tube
Step 1: Write down the given values
- Density of the liquid, ρ=0.4×103kg/m3
- Surface tension, T=0.05N/m
- Angle of contact, cosθ=0.4
- Acceleration due to gravity, g=10m/s2
- Radius of the capillary tube, R=0.2mm=0.2×10−3m
Step 2: Substitute the values into the formula
Now, we substitute the values into the formula for h:
h=2×0.05×0.40.4×103×10×0.2×10−3
Step 3: Simplify the equation
Calculating the numerator:
2×0.05×0.4=0.04
Calculating the denominator:
0.4×103×10×0.2×10−3=0.4×103×10×0.2×10−3=0.4×10×0.2=0.008
Step 4: Calculate h
Now, substituting back into the equation for h:
h=0.040.008=5
Step 5: Convert to centimeters
Since the height is in meters, we convert it to centimeters:
h=5m=5cm
Final Answer
The height to which the liquid rises in the capillary tube is 5cm.
---
- h = height of the liquid column
- T = surface tension of the liquid
- θ = angle of contact
- ρ = density of the liquid
- g = acceleration due to gravity
- R = radius of the capillary tube
- Density of the liquid, ρ=0.4×103kg/m3
- Surface tension, T=0.05N/m
- Angle of contact, cosθ=0.4
- Acceleration due to gravity, g=10m/s2
- Radius of the capillary tube, R=0.2mm=0.2×10−3m
Now, we substitute the values into the formula for h:
Calculating the numerator:
Now, substituting back into the equation for h:
Since the height is in meters, we convert it to centimeters:
The height to which the liquid rises in the capillary tube is 5cm.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - B
Explore 23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - C
Explore 15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:TRY YOURSELF
Explore 41 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment(Section-D)
Explore 14 Videos
Similar Questions
To what height does the liquid rise in a capillary tube of radus 0.25 mm, when dipped in a liquid of density 0.8×103kgm−3 and surface tension 0.05 N m−1? Given (cosθ=0.4)
View SolutionA liquid of density 103kgm3 and coefficient of viscosity 8 xx10^(-2) decapoise is flowing in a tube of radius 2 cm with speed 2 m/s. The. Reynold’s number is
View Solution
Knowledge Check
If the surface tension of water is 0.06 N/m, then the capillary rise in a tube of diameter 1mm is (θ=0∘)
A1.22 cmB2.44 cmC3.12 cmD3.86 cmThe rise in the water level in a capillary tube of radius 0.07 cm when dipped veryically in a beaker containing water of surface tension 0.07Nm−1 is (g = 10ms−2)
A2 cmB4 cmC1.5 cmD3 cm
Find the total pressure inside a sperical air bubble of radius 0.2 mm. The bubble is at a depth 5 cm below the surface of a liquid of density 2×103 kg m−3 and surface tension 0.082 N m−1. (Given : atmospheric pressure = 1.01 ×105Nm−2)
Hint : Pi=Po+2SR
Po = atmospheric pressure + gauge pressure of liquid column.
View SolutionCalculate the height to which water will rise in a capillary tube of diameter 1×10−3m [given surface tension of water is 0.072Nm−1 angle of contact is 0∘,g=9.8ms−2 and density of water =1000kgm−3]
View SolutionA piece of metal weighs 46 g in air and 30 g in liquid of density 1.24×103kgm−3 kept at 270C. When the temperature of the liquid is raised to 420C, the metal piece weights 30.5 g . The density of the liquid at 420C is 1.20×103kgm−3. Calculate the coefficient of linear expansion of the metal.
View SolutionCalculate the pressure indise a small air bubble of radius 0.01mm situated at a depth of h=20m below the fre surface of liquid of density ρ1=103kg/m3,ρ2=800km/m3 and surface tension T2=7.5×10−2N/m. The thickness of the first liqid is h1=15m and h2=25m.
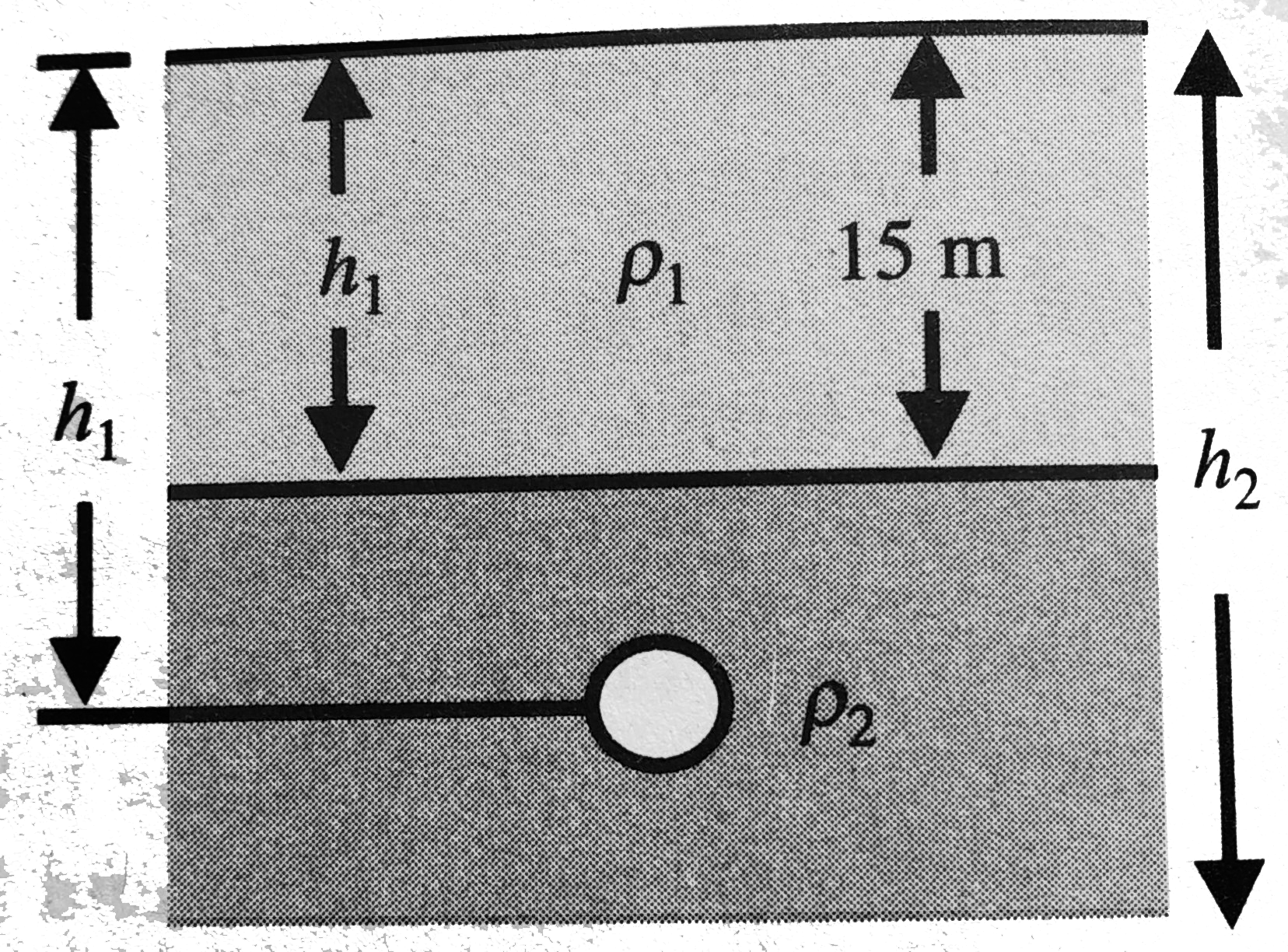
View SolutionA capillary of radius 0.15mm is dipped in liquid of density 'rho' = 667 kg/m^3. If surface tension of liquid is 120Nm then find height upto which liquid rises in capillary. Angle of contact between liquid and capillary tube is 60∘. (g=10ms2)
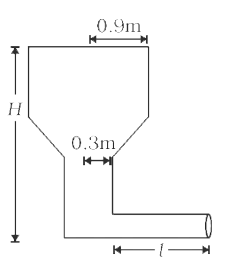
View SolutionA liquid of density 900 kg/m3 is filled in a cylindrical tank open from top of upper radius 0.9 m and lower radius 0.3 m. A capillary tube of length l is attached at the bottom of the tank as shown in the figure. The capillary has outer radius 0.002 m and inner radius a.
When pressure p is applied at the top of the tank volume flow rate of the liquid is 8×10−6m3/s and if capillary tube is detached, the liquid comes out from the tank with a velocity 10 m/s
[Given : πa2=10−6m2anda2/1=2×10−6m]
Determine the coefficient of viscosity in SI units when the capillary tube is attached :
View Solution