Two water pipes P and Q having diameters 2×10−2m and 4×10−2m, respectively, are joined in series with the main supply line of water. The velocity of water flowing in pipe P is
Four times that of Q
Two times that of Q
5times that of Q
3 times that of Q
To solve the problem, we will use the principle of conservation of mass, which is represented by the equation of continuity for incompressible fluids. The equation states that the product of the cross-sectional area (A) and the velocity (V) of the fluid must remain constant along a streamline.
1. Identify the diameters of the pipes:
- Diameter of pipe P, DP=2×10−2m
- Diameter of pipe Q, DQ=4×10−2m
2. Calculate the radii of the pipes:
- Radius of pipe P, rP=DP2=2×10−22=1×10−2m
- Radius of pipe Q, rQ=DQ2=4×10−22=2×10−2m
3. Use the equation of continuity:
The equation of continuity states that:
AP⋅VP=AQ⋅VQ
where A is the cross-sectional area and V is the velocity.
4. Calculate the cross-sectional areas of the pipes:
The cross-sectional area A of a cylindrical pipe is given by:
A=πr2
- Area of pipe P:
AP=π(rP)2=π(1×10−2)2=π×1×10−4m2
- Area of pipe Q:
AQ=π(rQ)2=π(2×10−2)2=π×4×10−4m2
5. Substituting the areas into the continuity equation:
π(1×10−4)VP=π(4×10−4)VQ
We can cancel π from both sides:
(1×10−4)VP=(4×10−4)VQ
6. Rearranging the equation to find the relationship between VP and VQ:
VP=4VQ
Conclusion:
The velocity of water flowing in pipe P is 4 times that of the velocity in pipe Q.
Final Answer:
VP=4VQ
---
- Diameter of pipe P, DP=2×10−2m
- Diameter of pipe Q, DQ=4×10−2m
- Radius of pipe P, rP=DP2=2×10−22=1×10−2m
- Radius of pipe Q, rQ=DQ2=4×10−22=2×10−2m
The equation of continuity states that:
AP⋅VP=AQ⋅VQ
where A is the cross-sectional area and V is the velocity.
The cross-sectional area A of a cylindrical pipe is given by:
A=πr2
- Area of pipe P:
AP=π(rP)2=π(1×10−2)2=π×1×10−4m2
- Area of pipe Q:
AQ=π(rQ)2=π(2×10−2)2=π×4×10−4m2
π(1×10−4)VP=π(4×10−4)VQ
We can cancel π from both sides:
(1×10−4)VP=(4×10−4)VQ
VP=4VQ
The velocity of water flowing in pipe P is 4 times that of the velocity in pipe Q.
VP=4VQ
Similar Questions
Two water pipes of diameters 2 cm and 4 cm are connected with the main supply line. The velocity of flow of water in the pipe of 2 cm
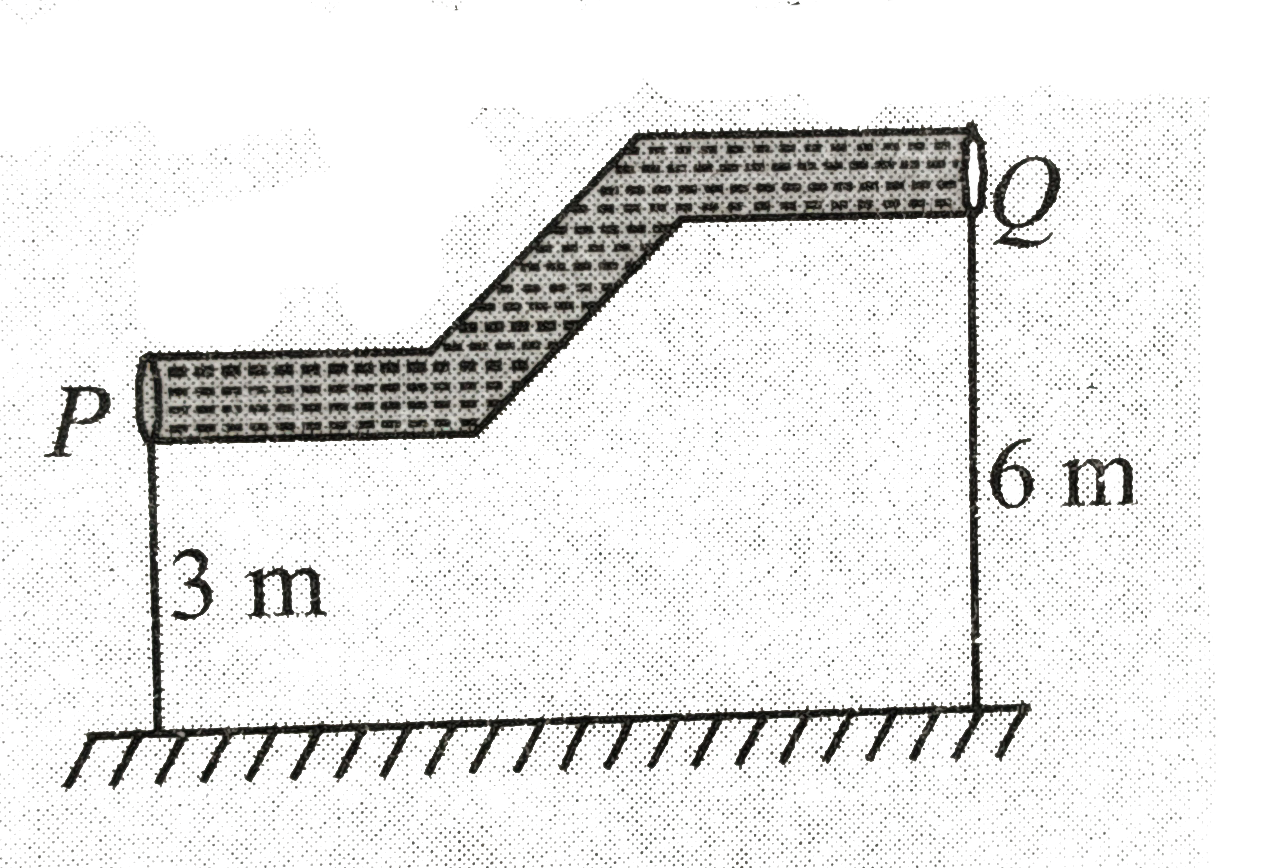
View SolutionA non-viscous liquid of constant density 500kg/m3 flows in a variable cross-sectional tube. The area of cross section of the tube at two points P and Q at heights of 3m and 6m are 2×10−3m3 and 4×10−3m3, respectively. Find the work done per unit volume by the forces of gravity as the fluid flows from point P to Q.
View SolutionA 3.6m long vertical pipe resonates with a source of frequency 212.5Hz when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height H(≈3.6m). A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of H. If the radii of the pipe and the hole are 2×10−2m and 1×10−3m respectively, Calculate the time interval between the occurance of first two resonances. Speed of sound in air 340m/s and g=10m/s2.
View SolutionThe reading of a pressure meter attached to a horizontal closed pipe is 3×105Nm−2. This reading falls to 1×105Nm−2 when the valve is opened. What is the speed of water flowing in the pipe?
View SolutionOne end of a horizontal pipe is closed with the help of a velve and the reading of a barometer attached in the pipe is 3×105 pascal When the value in the pipe is opened then the reading of barometer falls to 105 pascal the velocity of water flowing through the pipe will be in m/s-
View Solution_S01_052_Q01.png)
The pressure of water in a water pipe when tap is opened and closed is respectively 3×105Nm−2 and 3.5×105Nm−2 with open tap the velocity of water flowing is
(a). 10m/s
(b). 5m/s
(c). 20m/s
(d). 15m/s
View SolutionWhen a tap is closed, the manometer attached to the pipe reads 3.5×105Nm−2. When the tap is opened, the reading of manometer falls to 3.0×105Nm−2. The velocity of water in the pipe is
View SolutionTwo elastic bodies P and Q having equal mases are moving along the same line with velocities of 16 m/s and 10 m/s respectively. Their velocities after the elastic collision will be in m/s :
View SolutionThe reading of pressure-meter fitted in a closed pipe is 4.5×105Nm−2 . On opening the value of the pipe, the reading the meter reduces to 4×105Nm−2. Calculate the speed of water flowing in the pipe.
View SolutionWater is flowing through two horizontal pipes of different diameters which are connected together. The diameters of the two pipes are 3 cm and 6 cm respectively. If the speed of water in the narrower tube is 4ms−1. Then the speed of water in the wider tube is
View Solution
