A metallic tape gives correct value at 25∘C.A piece of wood is being measured by this metallic tape at 10∘C. The reading is 30 cm on the tape, the real length of wooden piece must be
30cm
>30cm
<30cm
Data is not sufficient
To find the real length of the wooden piece measured by a metallic tape at a different temperature, we can follow these steps:
1. Identify the Given Values:
- Correct measurement temperature (T₀) = 25°C
- Measurement temperature (T) = 10°C
- Reading on the tape (L₁) = 30 cm
2. Calculate the Change in Temperature (ΔT):
ΔT=T₀−T=25°C−10°C=15°C
3. Understand the Relation Between Lengths:
The relationship between the final length (L_f) at temperature T₀ and the original length (L₀) at temperature T can be expressed as:
Lf=L₀(1+αΔT)
where α is the coefficient of linear expansion.
4. Express the Ratio of Lengths:
Rearranging the equation gives:
LfL₀=1+αΔT
Here, L_f is the length at 25°C (correct measurement) and L₀ is the length at 10°C (the reading on the tape).
5. Substituting Known Values:
Since we know that the reading on the tape (30 cm) corresponds to L₀, we can express L_f as:
Lf=30 cm×(1+α×15)
6. Determine the Real Length:
Since we don't have the exact value of α, we can conclude that:
Lf>30 cm
This indicates that the real length of the wooden piece is greater than 30 cm due to the expansion of the tape at the higher temperature.
7. Conclusion:
The real length of the wooden piece must be greater than 30 cm.
Final Answer:
The real length of the wooden piece must be greater than 30 cm.
---
- Correct measurement temperature (T₀) = 25°C
- Measurement temperature (T) = 10°C
- Reading on the tape (L₁) = 30 cm
ΔT=T₀−T=25°C−10°C=15°C
The relationship between the final length (L_f) at temperature T₀ and the original length (L₀) at temperature T can be expressed as:
Lf=L₀(1+αΔT)
where α is the coefficient of linear expansion.
Rearranging the equation gives:
LfL₀=1+αΔT
Here, L_f is the length at 25°C (correct measurement) and L₀ is the length at 10°C (the reading on the tape).
Since we know that the reading on the tape (30 cm) corresponds to L₀, we can express L_f as:
Lf=30 cm×(1+α×15)
Since we don't have the exact value of α, we can conclude that:
Lf>30 cm
This indicates that the real length of the wooden piece is greater than 30 cm due to the expansion of the tape at the higher temperature.
The real length of the wooden piece must be greater than 30 cm.
The real length of the wooden piece must be greater than 30 cm.
Similar Questions
A steel tape gives corrent measurement at 20∘C. A piece of wood is being measured with the steel tape at 0∘C.The reading is 25 cm on the tape. The real length of the given pices of wood must be
View SolutionA steel tape is correctly calibrated at 20∘C and is used to measure the length of a table at 30∘C. Find the percentage error in the measurement of length. [αsteel=11×10−5/.∘C]
View SolutionA surveyor's 30 m steel tape is correct at a temperature of 20∘C. The distance between two points, as measured by this tape on a day when the temperature is 35∘C. Is 26m. What is the true distance between the point?
(asteel=1.2×10−5∘C)
View SolutionA steel tape 1m long is correctly calibrated for a temperature of 27∘C. The length of a steel rod measured by this tape is found to be 63.0cm on a hot day when the temperature is 45.0∘C. What is the acutual length of the steel rod on that day? what is the length of the same steel rod on a day when the temperature is 27.0∘C ? coefficient of linear expansion of steel =1.20×10−5.∘C−1.
View SolutionA steel tape measures that length of a copper rod as 90.0 cm when both are at 10∘C, the calibration temperature, for the tape. What would the tape read for the length of the rod when both are at 30∘C. Given αsteel=1.2×10−5 per.∘CandαCu=1.7×10−5per.∘C
View SolutionA metal rod AB of length 10x has it one end in ice at 0∘C and the other end B in water at 100∘C If a point P on the rod is maintained at 400∘C then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of melting of ice is 80cal/g If the point P is at a distance of λx from the ice end A find the value of λ [neglect any heat loss to the surrounding] .
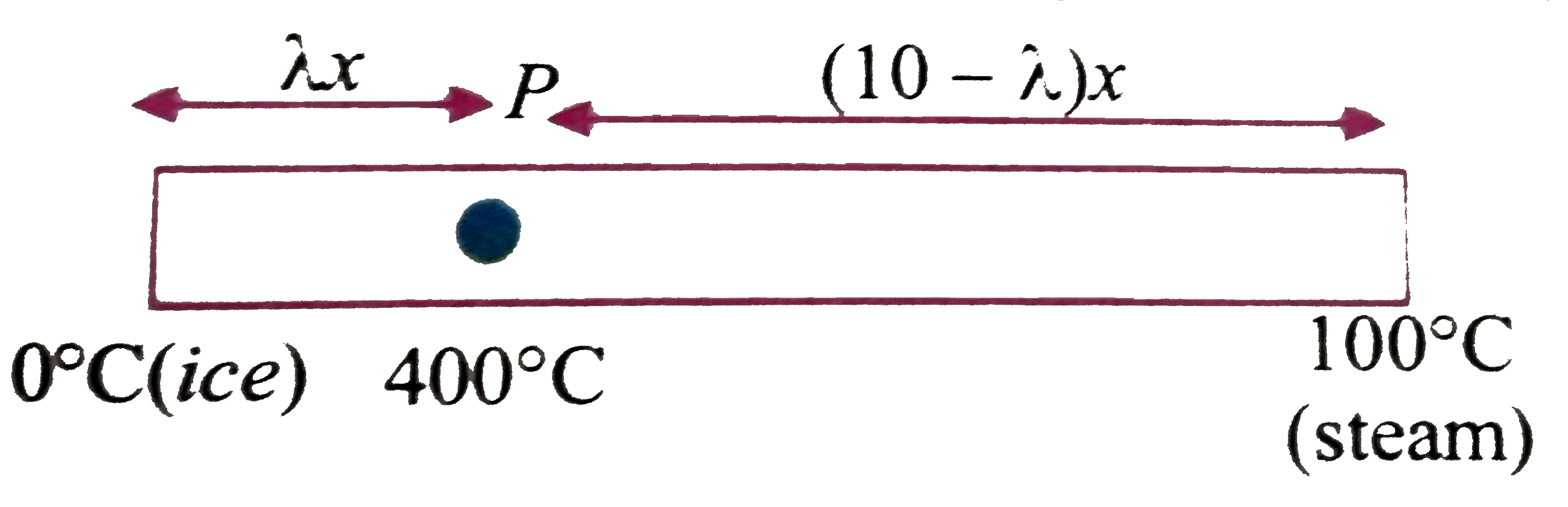 .
.
View SolutionA steel ruler exactly 20cm long is graduated to give correct measurements at 20∘C.
(a) Will it give readings that are too long or too short at lower temperatures?
(b) What will be that actual length of the ruler when it is used in the desert at a temperature of 40∘C ? αsteel=1.2×10−5(.∘C)−1 .
View SolutionA steel rular exactly 20cm long is graduated to give correct measurements at 20∘C.
(a) Will it give readings that are too long or too short at lower temperatures?
(b) What will be that actual length of the rular when it is used in the desert at a temperature of 40∘C ? αsteel=1.2×10−5(.∘C)−1 .
View SolutionAt room temperature (25∘C) the length of a steel rod is measured using a brass centimetre scale. The measured length is 20 cm. If the scale is calibrated to read accurately at temperature 0∘C, find the actual length of steel rod at room temperature.
View Solution(a) The brass scale of a barometer gives correct reading at 0∘C . Coefficient of linear expansion of brass is 2.0×10−5/∘C . The barometer reads 75cm at 27∘C . What is the atmospheric pressure at 27∘C ?
(b) A barometer reads 75.0cm on a steel scale. The room temperature is 30∘C . The scale is correctly graduated for 0∘C . The coefficient of linear expansion of steel is α=1.2×10−5/∘C and the coefficient of volume expansion of mercury is γ=1.8×10−4/∘C . Find the correct atmospheric pressure.
View Solution
