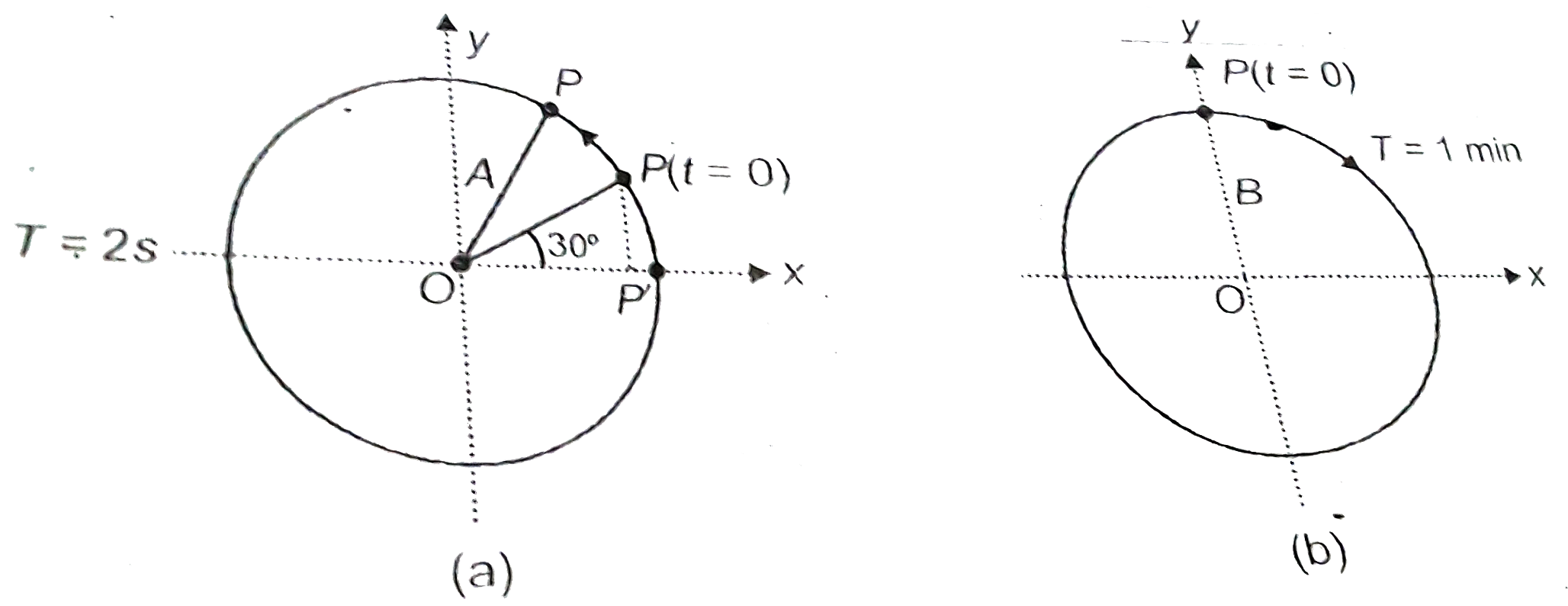
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
(a) At t=0 , OP makes anangleof 30∘=π6 rad with the positive direction of x-axid. After time t, it covers an angle 2πTt in anticlockwise direction, and makes an angle of 2πTt+π6 with the x-axis.
The projection of OP on the x-axis at time t is given by x(t)=Acos(2πTt+π6)
Fort=2s
x(t)=Acos(2π2t+π6)
Which is an SHM of amplitude A, period 2s, and an initial phase =π6
(b) At t=0, OP makes an angle of 90∘=π2 with the x-axis . After time t, it covers anangle of 2πTt, in the clockwise direction and makes an angle of (π2−2πTt) with the x-axis . The projection of OP on x-axis at time t, is given by
x(t)=Bcos(π2−2πTt)
=Bsin(2πTt)
For T= 1 min = 60s
x(t)=Bsin(π30t)
Writing this as x(t)=Bcos(π30t−π2) ( as cos(−θ)=cosθ and cos(90∘−θ)=sinθ) and comparing it with equation (ii),x(t)=Acos(ωt+ϕt), we find that this represents SHM of amplitude B, period 60s , and initial phase of (−π2)
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercise18videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)60videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-J )8videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)4videos
PHYSICAL WORLD
Similar Questions
The following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
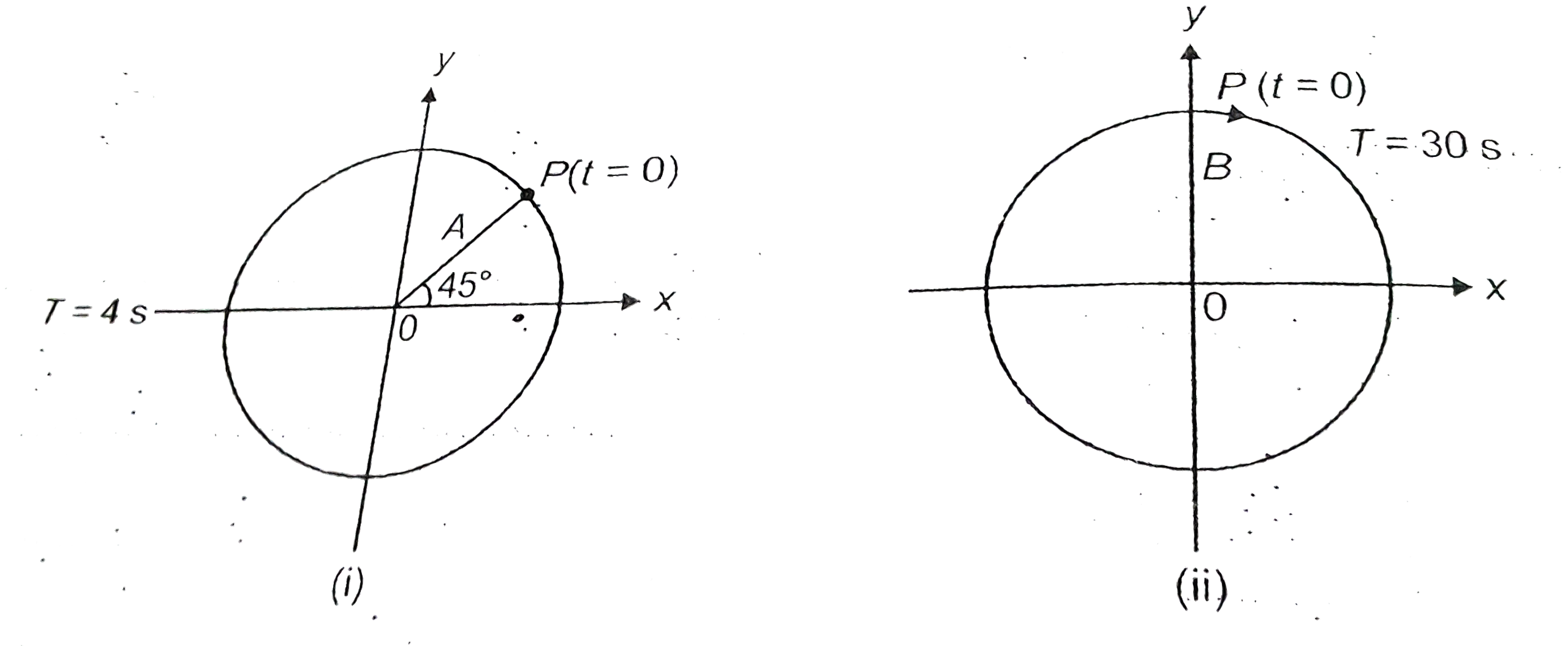 View Solution
View SolutionThe radius of cirlcue, the period of revolution, initial position and sense of revolution are indicated in the figure.

y-projection of the radius vector of rotating particle P is :View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
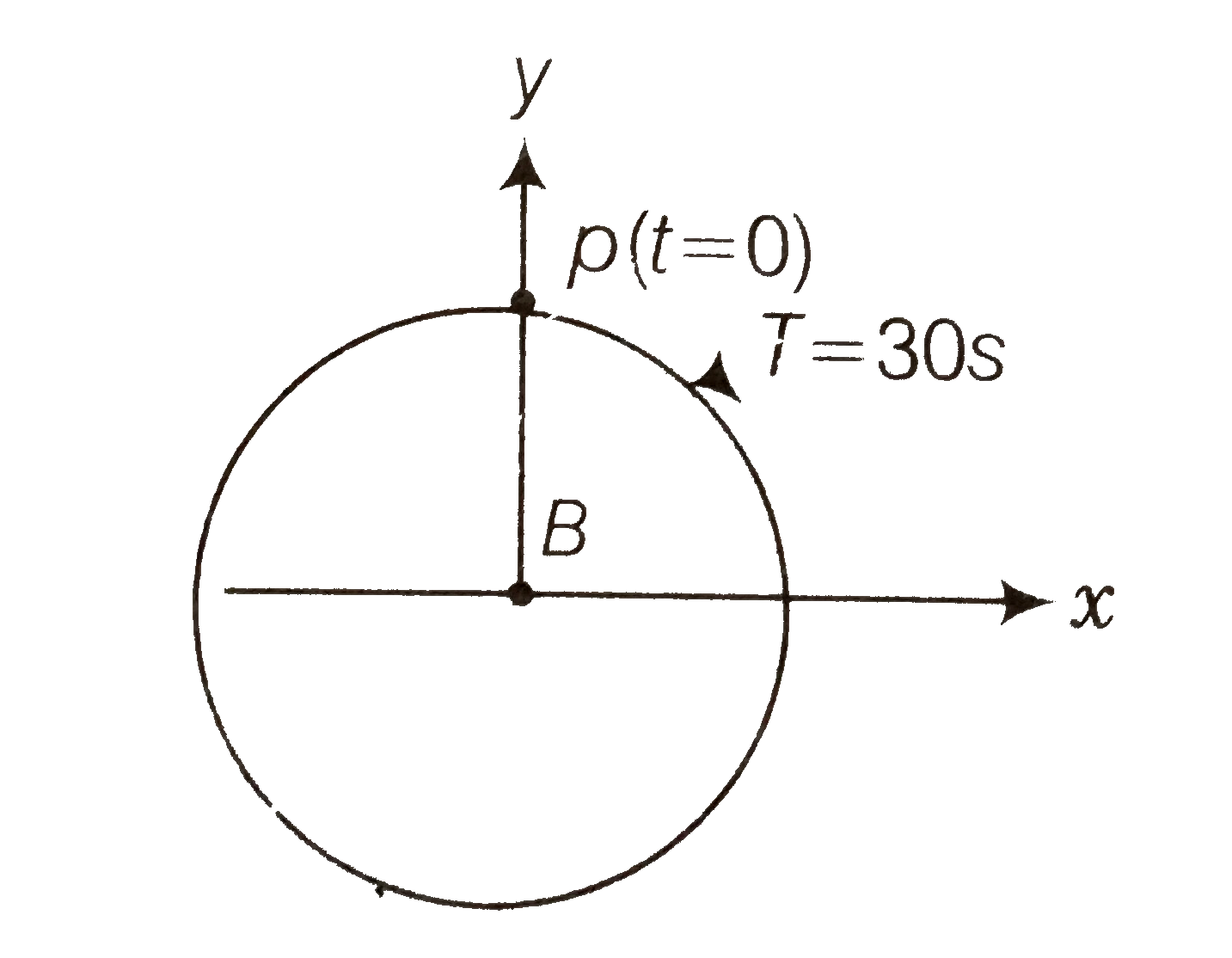 View Solution
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
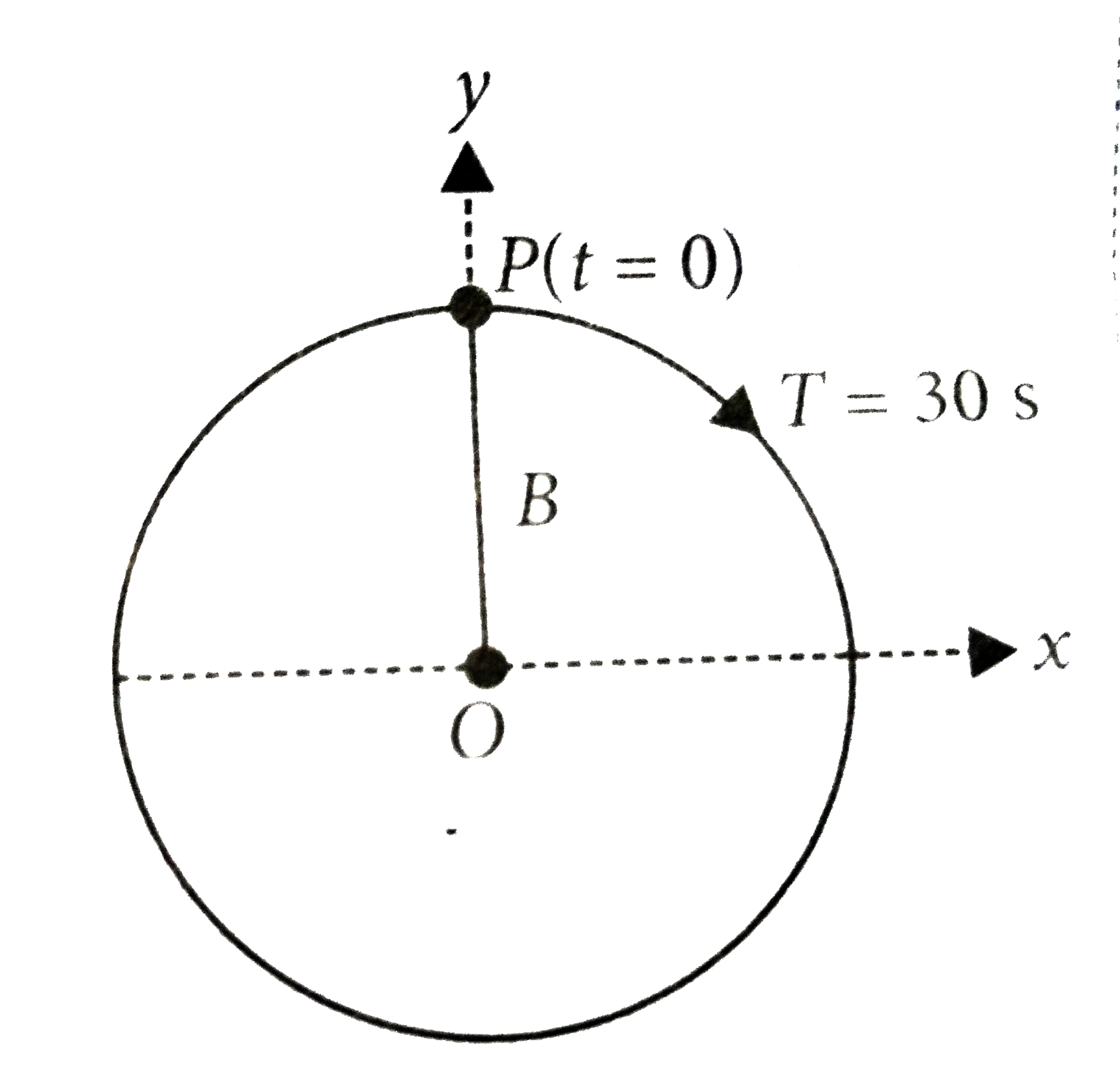 View Solution
View Solution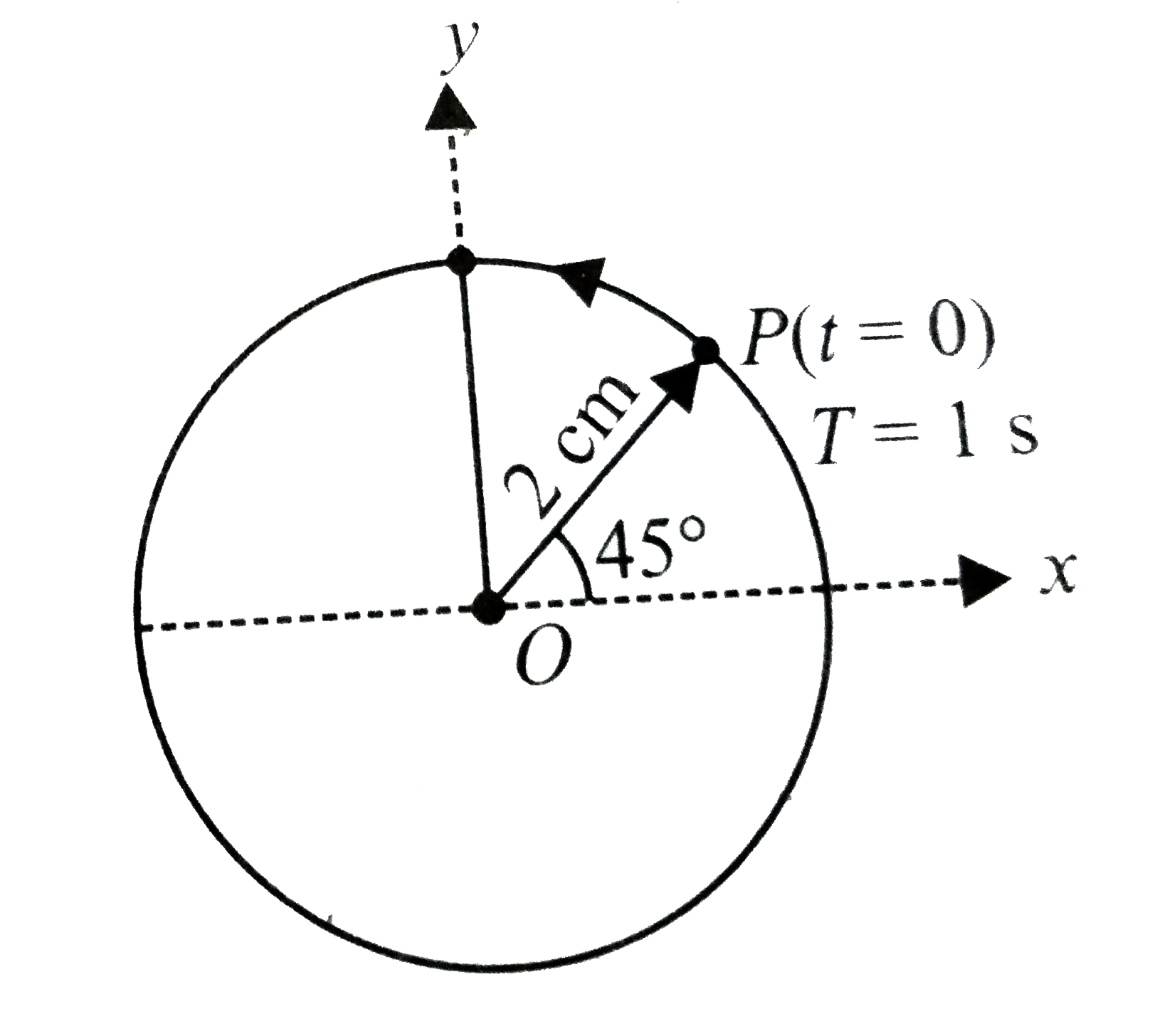
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial positionn are indicated in the figure. The simple harmonic motion off the x-projection of the radius vector of the rotating particle P isView SolutionInitial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle :
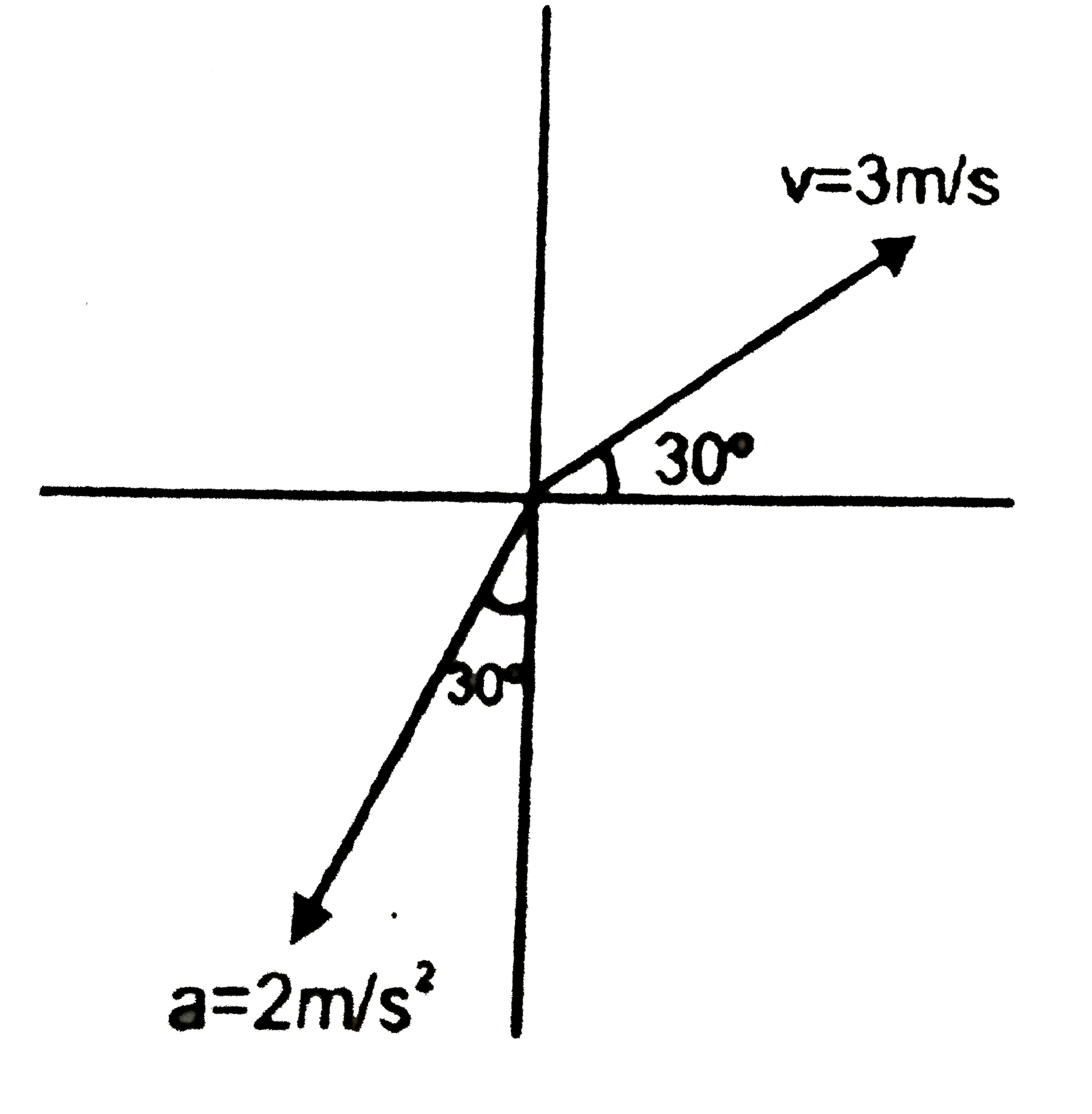 View Solution
View SolutionA particle moves in a circle of radius R. In half the period of revolution its displacement is ………… and distance covered is ………. .
View SolutionRead each statement below carefully and state, with reasons, if it is true or false :
(a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the center.
(b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.
(c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.View Solution(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
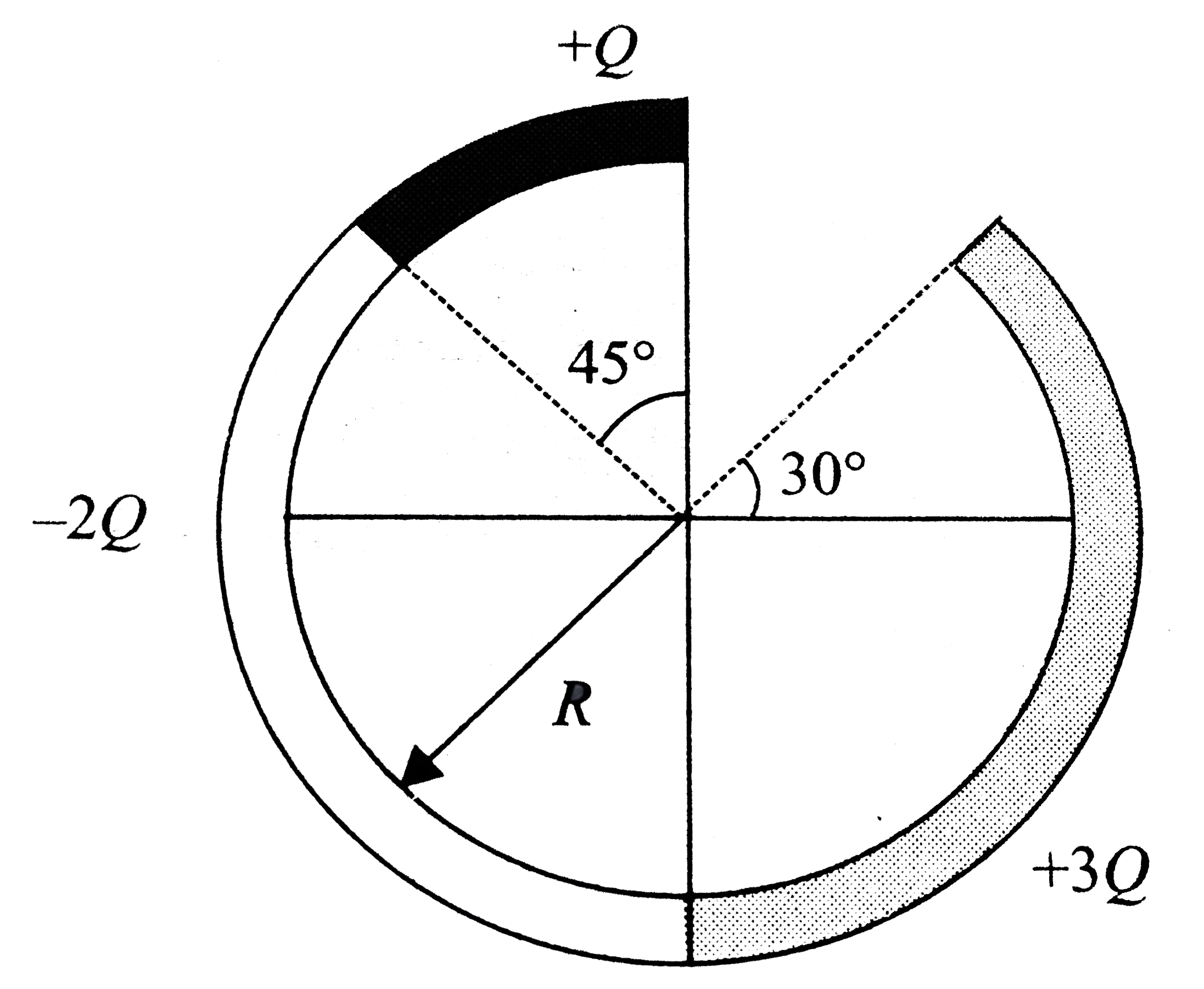 .View Solution
.View SolutionA particle of mass m , initial speed u and angle of projection θ is projected as shown in the figure. Average torque on the projectile between initial and final positions P and Q about the point of projection is
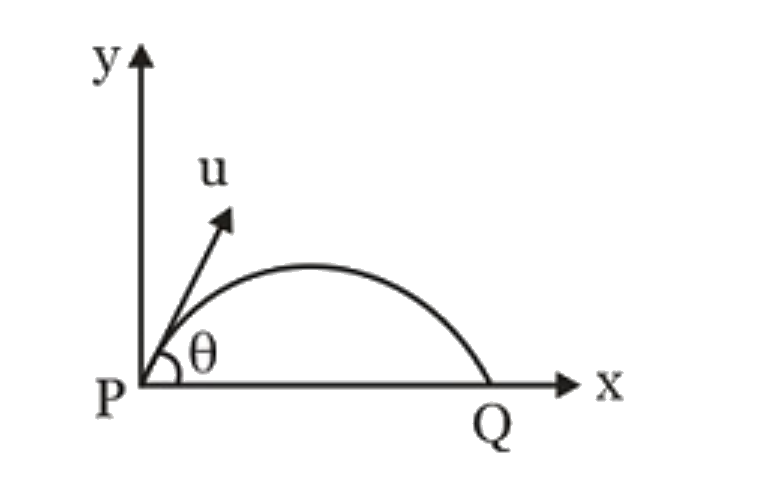 View Solution
View Solution
